Слайд 2
Большие объекты
Большие (массивные) объекты (large objects - LOBs):
большие двоичные объекты (BLOBs) и большие символьные объекты (CLOBs)
Для
‘стандартной’ СУБД: LOB - одно поле без внутренней структуры
Традиционные реляционные СУБД имеют ограничение на максимальную длину поля (например, 255 байт или 32767 байт)
Мультимедийные объекты как правило имеют значительно больший размер
Слайд 3
Большие объекты
Современные СУБД поддерживают поля длиной до 4ГБ,
тем не менее:
Большие объекты могут не помещаться полностью в
общей памяти
Необходима фрагментарная обработка (прямой доступ к отдельным фрагментам хранимого объекта): нерационально извлекать весь объект, если нужен только один его фрагмент
Доступ к объекту согласно его логической структуре осуществляется программными средствами более высокого уровня
Вспомогательная система хранения более универсальна: страницы с различной емкостью и разные по размерам кластеры страниц улучшат операции ввода/вывода для объектов переменной длины
Необходимо вести лог-файл (восстановление данных после ошибки): протоколирование всего объекта неэффективно, ведь только малая часть может быть повреждена
Слайд 4
Большие объекты
SQL и поля большого размера:
Типы полей: символьные
(CLOB) и двоичные (BLOB)
Следующие операции возможны:
Конкатенация (concatenation)
Извлечение
подстроки (substring)
Наложение (overlay): замена подстрок
Триммирование: удаление определенных символов (например, пробелов) в начале и конце строки
Определение позиции заданной подстроки внутри строки
Не разрешены:
GROUP BY, ORDER BY, операции над множествами (UNION, INTERSECT)
Слайд 5
Двухуровневое разбиение
Пример архитектуры: система хранения данных Wisconsin Storage
System (WiSS) [1]; реализована в нескольких СУБД, в частности,
в прототипах объектно-ориентированных СУБД
Позволяет хранить текстовые поля переменной длины и изображения
Реализована в Unix-среде (но в обход файловой системы, т.к. хранение в последней осуществляется на физически разбросанных по дисковому пространству страницах небольшого размера)
WiSS имеет свою собственную независимую от Unix буферизацию
Поле большого размера являются частью записи (в бд) на логическом уровне, но физическое хранение обособлено
Поле большого размера в WiSS состоит из:
Блоков (slices в оригинальной работе) данных на которые разбивается поле; размер блока ограничен размером страницы; последний блок (меньше размера страницы) называется ‘крошка’ (crumb в ориг.работе)
Директории, содержащей ссылки на блоки
Слайд 6
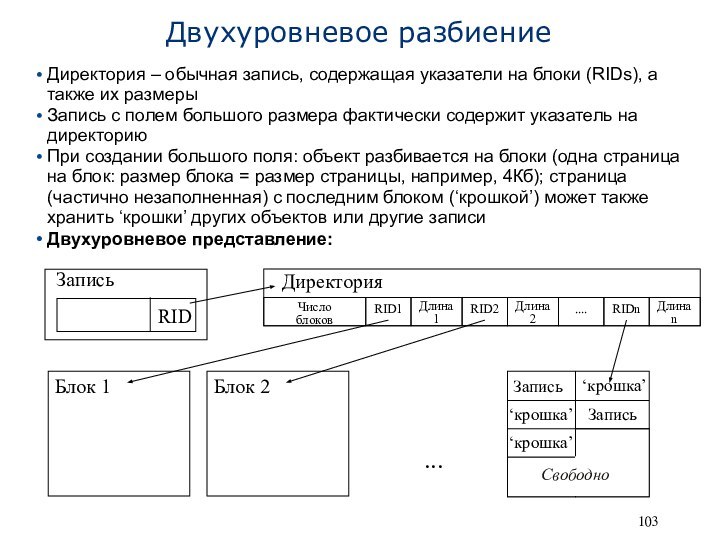
Двухуровневое разбиение
Директория – обычная запись, содержащая указатели на
блоки (RIDs), а также их размеры
Запись с полем большого
размера фактически содержит указатель на директорию
При создании большого поля: объект разбивается на блоки (одна страница на блок: размер блока = размер страницы, например, 4Кб); страница (частично незаполненная) с последним блоком (‘крошкой’) может также хранить ‘крошки’ других объектов или другие записи
Двухуровневое представление:
Запись
RID
...
Блок 1
Запись
‘крошка’
Число
блоков
Директория
RID1
Длина 1
RID2
Длина 2
RIDn
....
Длина n
Блок 2
Запись
‘крошка’
‘крошка’
Свободно
Слайд 7
Двухуровневое разбиение
Операции с полями большого размера:
Извлечь N
байт, начиная с позиции S:
Определить блок, содержащий позицию S:
find Max k such that length[1]+…+length[k-1]Извлечь блоки k, k+1, … до тех пор пока не будет извлечено N байт или не достигнут конец поля
Вставить N байт, начиная с позиции S:
Определить нужный блок (см.выше)
Записать N байт после позиции S на странице с данным блоком, если на странице есть место для N байт; иначе разбить блок на позиции S
Выделить достаточное количество новых страниц между двумя образовавшимися блоками
Записать N байт в две ‘расщепленные’ страницы и выделенные новые страницы (равномерно распределяя нагрузку на страницы)
Внести изменения в директорию
Слайд 8
Двухуровневое разбиение
Операции с полями большого размера:
Удалить N
байт, начиная с позиции S:
Определить затрагиваемые страницы
Удалить N байт,
высвободить пустые страницы
Объединить первый и последний затронутый блоки на одной странице, если возможно
Внести изменения в директорию
Слайд 9
Двухуровневое разбиение
Размер хранимого поля:
В WiSS директория может занимать
не более чем одну страницу
Для страниц размером 4Кб: директория
может содержать примерно 400 пар «размер блока,указатель на блок». Таким образом, верхний предел размера для поля – 1.6Мб. Достаточно для текста и большинства графических изображений, но не для аудио и видео.
Для 8Кб-страниц: максимальный размер поля - 6.4Мб (800*8Кб)
Страницы большого размера неэффективны (значительная фрагментация вследствие обновлений)
Очевидный обходной путь: дробление поля большого размера на несколько подполей максимально возможного размера (например, по 1.6Мб в случае 4Кб-страниц)
WiSS не удовлетворяет требованиям многих мультимедийных приложений
Слайд 10
Улучшенное двухуровневое разбиение
Пример архитектуры: менеджер больших объектов Starburst
[2]; прототип экспериментальной СУБД, разработанный в IBM
Элегантная и весьма
быстрая двухуровневая схема для полей большого размера
Идея: хранить поле на нескольких физически смежных сегментах переменной длины; при этом размеры сегментов задаются экспоненциальной функцией (далее подробнее)
Размеры сегментов с данными не произвольны, указатели на сегменты также не произвольны
Слайд 11
Улучшенное двухуровневое разбиение
Система ‘близнецов’ (buddy system)
[3]:
Пространство ‘близнецов’ состоит из 2n страниц, сегментам
размером в 2k страниц разрешено иметь адреса 0, 2k, 2*2k, 3*2k, ... (т.е. адрес таких сегментов кратен 2k)
Два соседних сегмента одного и того же размера в 2k страниц называются близнецами, если их объединение (сегмент размером в 2k+1 страниц) имеет разрешенный адрес
Например, сегменты 1,2 и 3,4 – близнецы, а сегменты 2,3 нет:
Для каждого сегмента адрес его близнеца определяется XORом (операцией ‘исключающее ИЛИ’) адреса сегмента и размера сегмента
Практическое достоинство: более короткие указатели, т.к. число возможных размеров сегментов ограничено
Слайд 12
Улучшенное двухуровневое разбиение
Организация памяти в Starburst:
Вся имеющаяся память
представлена несколькими дисковыми пространствами (например, физический диск - пространство)
Каждое
из пространств содержит массив пространств близнецов
Пространство близнецов состоит из:
Управляющей страницы (подробно о ее структуре в [2])
2n страниц с данными (сгруппированные в сегменты)
Управляющая страница содержит:
Количество свободных сегментов каждого размера (размеры сегментов фиксированы - 1, 2, 4, 8, …, 2n страниц)
Указатели на свободные сегменты (точнее, на позиции, начиная с которых могут находиться свободные сегменты данного размера)
2n
2n-1
42n-4
32n-3
52n-4
Управл.
страница
Сегмент
Слайд 13
Улучшенное двухуровневое разбиение
Выделение места:
Выбрать наиболее подходящий сегмент
Если сегмент
слишком большой, то разбить его пополам, возможно несколько раз;
добавить остающиеся части (сегменты меньших размеров) в списки свободных сегментов
Освобождение сегмента:
Проверить близнеца; если он свободен, объединить сегменты (и повторить данный шаг)
Внести изменения в управляющей странице (сегменты, которые были объединены, удалить из списков, а объединенный (возможно неоднократно) сегмент добавить в списки свободных сегментов
Обновление данных:
Поддерживается только добавление данных в конец (актуально для хранения лог-файлов)
Проблема фрагментации (типичная проблема для системы близнецов) частично решается за счет разбиения большого объекта на несколько частей
Для любого поля большого размера вследствие фрагментации теряется не более одной страницы
Слайд 14
Улучшенное двухуровневое разбиение
Дескриптор поля большого размера в
Starburst:
Дескриптор представляет собой директорию указателей на сегменты с данными
в пространстве близнецов
Размер дескриптора не более 255 байт; хранится в записи, имеющей поле большого размера
Дескриптор содержит:
Идентификатор дискового пространства
Размер поля (в байтах)
Число сегментов
Размеры первого и последнего сегмента (компактно в виде log2(size))
Указатели (относительные) на сегменты (не более 80)
Слайд 15
Улучшенное двухуровневое разбиение
Создание поля большого размера:
Если размер (поля)
известен, с самого начала использовать достаточно большие сегменты
Если размер
неизвестен, выделять сегменты с последовательно удваивающимся размером: размером в 1 страницу, в 2 страницы, в 4, в 8 и т.д. до тех пор пока поле не окончится или пока не будет достигнут максимальный размер сегмента; последовательность сегментов максимального размера выделяется до тех пор пока все поле не сохранено
Последний выделенный сегмент обрезается по ближайшей границе: например, для хранения данных размером в 11 страниц сегмент размером в 16 страниц обрезается до смежных сегментов размером в 8, 2 и 1 страницы (1110 = 23*1 + 21*1 + 20*1 11012); сегменты размером в 1 и 4 страницы высвобождаются
Для 4Кб-страницы и максимального размера сегмента в 8Мб, максимальный размер поля – 448Мб
Менеджер больших объектов Starburst приспособлен для быстрой последовательной обработки таких данных как изображения, аудио и видео
Слайд 16
Древовидное представление
Многоуровневая директория: нет ограничений на число уровней
Пример
архитектуры: система хранения данных EXODUS [4]
Чрезвычайно гибкая система управления
большими объектами; добавление и удаление данных с любой позиции внутри объекта
Скорость последовательной обработки данных невысока
Каждый объект имеет уникальный идентификатор – OID = <номер страницы,номер слота>
Два типа объектов:
Маленькие объекты: помещаются на одной странице
Большие объекты: занимают несколько страниц, OID указывает на заголовок
Два типа страниц:
Сегментированная страница: содержит маленькие объекты и заголовки больших объектов
Остальные страницы содержат части больших объектов (каждая из таких страниц соответствует только одному объекту)
Маленький объект, превысивший размер страницы, автоматически преобразуется в большой объект
Слайд 17
Древовидное представление
Физическое представление объекта: B+-дерево с индексом по

байтовым позициям внутри объекта
Корень дерева: заголовок большого объекта
Каждый внутренний
узел: содержит пары <смещение,указатель> для каждого своего потомка
Смещение: максимальное число байт, содержащееся в поддереве, корнем которого является потомок
Указатель: адрес страницы
Смещение для крайнего правого потомка показывает размер части объекта, определяемого поддеревом, корнем которого является данный узел. Соответственно, в случае корня дерева смещение для крайнего правого потомка даст размер всего объекта.
Число пар <смещение,указатель> в узле – от k до 2k+1 (т.е. узел как минимум наполовину заполнен), где k – параметр B+-дерева.
Внутренние узлы могут занимать не более одной страницы.
Лист (узел на последнем уровне дерева): одна или несколько физически смежных страниц (количество страниц на лист задается системным параметром); содержит только данные; лист должен быть заполнен не менее чем на половину.
Слайд 18
Древовидное представление
Рисунок взят из [4]
Левый узел содержит байты
1-421, правый узел – остаток объекта (байты 422-786). Крайний
правый лист содержит 173 байта данных. 50-ый байт в этом листе является 192+50=242-ым байтом в крайнем правом узле и 421+242=663-им байтом в целом объекте.
Максимально возможные размеры объекта в случае 4Кб-страниц, 4-байтных указателей и смещений, и 4-х страничных листьев:
Двухуровневое дерево: 8Мб
Трехуровневое дерево: 4Гб
Слайд 19
Древовидное представление
Обозначения:
Смещения - c[i], c[0] = 0; указатели
- p[i], 1 i 2k+1
Поиск:
Извлечь
N байт, начиная с позиции S
Алгоритм
Считываем страницу с корнем – P, присвоим: start = S.
До тех пор пока P не является листом выполняем следующее:
сохраняем адрес P в стеке;
находим наименьшее c[i], такое что start c[i];
присваиваем: start = start c[i-1];
считываем страницу, соответствующую p[i], которая становится P.
Достигнув листа, первый нужный байт находится на странице P на позиции start.
Для получения остальных N байт, путешествуем по дереву, используя стек из шага 2.
Демонстрация (см.рисунок на пред.слайде): допустим нужны байты 250-300. start=250, ищем наименьшее смещение – c[1]=421. Далее start=250-c[0]=250, по p[1] считываем левый узел. Находим смещение – c[2]=282, start=250-c[1]=130. p[2] ведет к листу с 162 байтами. Извлекаем байты 130-162. Остающиеся 18 считываем с листа-соседа справа (добираемся до данного листа с помощью стека).
Слайд 20
Древовидное представление
Вставка:
Вставить N байт после позиции
S
Алгоритм
Находим лист L, содержащий байт
на позиции S, как было показано в предыдущем алгоритме. Во время движения по дереву обновить смещения, согласно ожидаемой вставке. Сохранить путь в стеке.
Если в L достаточно места для N байт, вставим их и завершим операцию.
Иначе, выделим достаточное число новых листьев и равномерно распределим старые байты листа L и N новых байт между листьями. Распространить новые смещения и указатели вверх по дереву с помощью стека. В случае если произойдет переполнение внутреннего узла, использовать тот же подход, что и при переполнении листа.
Замечание: коэффициент использования памяти можно улучшить если проверять правые и левые листья-соседи на наличие свободного места для вставляемых данных.
Слайд 21
Древовидное представление
Добавление в конец (специальный случай вставки):

Добавить N байт в конец объекта
Алгоритм
Двигаемся по
крайнему правому пути, прибавляя N к смещениям, и сохраняем путь в стеке.
Если в крайнем правом листе R достаточно места для N байт, добавим их и завершим операцию.
Иначе, считаем левого соседа R – лист L. Выделим достаточное число новых листьев, чтобы вместить содержимое листов R и L плюс новые N байт. Заполним все листья за исключением двух последних полностью, а два последних равномерно (таким образом, чтобы каждый из них был заполнен, по меньшей мере, наполовину). Распространить новые смещения и указатели вверх по дереву с помощью стека. Разрешать переполнения внутренних узлов также как и при вставке.
Замечание: преимущество данного алгоритма вставки в том, что он гарантирует наилучший коэффициент использования листьев в случаях, когда большие объекты создаются пошагово путем последовательных добавлений в конец (например, когда создаются сверх большие объекты).
Слайд 22
Древовидное представление
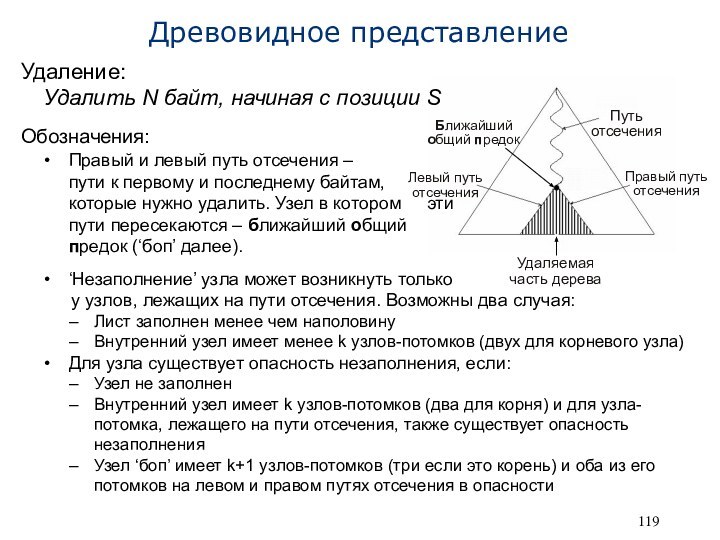
Удаление:
Удалить N байт, начиная с
позиции S
Обозначения:
Правый и левый путь отсечения –
пути к первому и последнему байтам, которые нужно удалить. Узел в котором эти пути пересекаются – ближайший общий предок (‘боп’ далее).
Удаляемая часть дерева
Путь отсечения
Правый путь отсечения
Левый путь отсечения
Ближайший общий предок
‘Незаполнение’ узла может возникнуть только
у узлов, лежащих на пути отсечения. Возможны два случая:
Лист заполнен менее чем наполовину
Внутренний узел имеет менее k узлов-потомков (двух для корневого узла)
Для узла существует опасность незаполнения, если:
Узел не заполнен
Внутренний узел имеет k узлов-потомков (два для корня) и для узла-потомка, лежащего на пути отсечения, также существует опасность незаполнения
Узел ‘боп’ имеет k+1 узлов-потомков (три если это корень) и оба из его потомков на левом и правом путях отсечения в опасности
Слайд 23
Древовидное представление
Алгоритм
Фаза удаления:
Двигаемся по
дереву по левому и правому путям отсечения. Запоминаем узлы,
лежащие на путях. Удаляем все поддеревья, содержащиеся целиком между левым и правым путям отсечения. Отражая удаление, обновляем смещения во всех узлах, лежащих на путях.
Фаза перебалансировки:
Если корневой узел не в опасности, перейти к шагу 2. Если у корня только один потомок, то делаем потомка корнем и переходим к шагу 1. Иначе, сливаем/перетасовываем те узлы-потомки, что находятся в опасности, и переходим к шагу 1.
Перейдем к следующему узлу-потомку, лежащему на пути отсечения. Если таких узлов не осталось, дерево перебалансировано.
До тех пор пока данный узел в опасности, сливаем/перетасовываем его с узлами-соседями (здесь потребуется 0, 1 или 2 итерации).
Перейдем к шагу 2.
Слайд 24
Древовидное представление
Замечания:
Представление данных в виде B+-деревьев довольно
эффективно на практике:
Коэффициент использования памяти – около 70% в
случае обычной вставки и около 80% с случае улучшенной вставки
Скорость поиска – десятки миллисекунд (в зависимости от скорости чтения данных на диске и буферизации)
Контроль версий для больших объектов:
Одинаковые части различных версий могут использоваться совместно
Обновления не затрагивают старые версии объекта: изменяемые узлы копируются на новое место и обновляются
Старые версии объекта не могут быть обновлены, но удаление старых версий возможно: при этом необходимо избегать удаление узлов, которые используются другими версиями объекта (простейший способ: пометить узлы всех остальных версий, а затем удалить все непомеченные узлы)
Слайд 25
Упражнения
В чем отличие B-дерева от B+-дерева?
Выполнить следующие операции
с объектом на слайде 16:
Вставить 201 байт, начиная с
позиции 200
(Вернувшись к начальному виду дерева) вставить 610 байт в конец объекта
Удалить байты на позициях 101-201
Удалить байты на позициях 280-501
Считаем при этом, что дерево имеет следующие
параметры:
Каждый узел может иметь не более трех потомков (k=1)
Емкость листа – 256 байт




![Организация и управление большими объектами Двухуровневое разбиениеПример архитектуры: система хранения данных Wisconsin Storage System (WiSS) [1]; реализована](/img/tmb/13/1291107/80ab94a78af79024c85b83d9c16a0251-720x.jpg)



![Организация и управление большими объектами Улучшенное двухуровневое разбиениеПример архитектуры: менеджер больших объектов Starburst [2]; прототип экспериментальной СУБД,](/img/tmb/13/1291107/2bc643a040b1e17b8066426317bea2e3-720x.jpg)
![Организация и управление большими объектами Улучшенное двухуровневое разбиение Система ‘близнецов’ (buddy system) [3]: Пространство ‘близнецов’](/img/tmb/13/1291107/557e9b2c4f345fcfc72837df6819a44a-720x.jpg)






![Организация и управление большими объектами Древовидное представлениеРисунок взят из [4]Левый узел содержит байты 1-421, правый узел –](/img/tmb/13/1291107/df7600e0ff6acc413a0fcc6b9212a389-720x.jpg)
![Организация и управление большими объектами Древовидное представлениеОбозначения:Смещения - c[i], c[0] = 0; указатели - p[i], 1 ](/img/tmb/13/1291107/044734b287bf1d08e1d1bf3f57835c92-720x.jpg)





![Организация и управление большими объектами Ссылки на литературу[1] Chou et al. Design and Implementation of the](/img/tmb/13/1291107/4146d5c36587950e0b2a44ed7c4aaa10-720x.jpg)





























