мышления. Она изучает абстрактное мышление как средство познания объективного
мира. Термин «логика» происходит от древнегреческого logos – «слово, мысль, понятие, рассуждение, закон».
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Основы логики
Содержание
- 2. Логика – это наука о законах и
- 3. Логика является одной из дисциплин, образующих математический
- 4. В вычислительной технике и автоматике используются логические
- 5. Этапы развития логикиПервые учения о формах и
- 6. В XVII веке немецкий ученый и философ
- 7. Алгебра логикиС точки зрения устройства ЭВМ нас
- 8. Примеры:Москва – столица РоссииСтудент математического факультета педагогического
- 9. Основные понятия логики:Утверждение – высказывание, которое требуется
- 10. Простые высказывания обозначают заглавными латинскими буквами A,
- 11. Примеры:Рассмотрим следующие высказывания:A = (7 > 3)B
- 12. Основная идея математической логики – в
- 13. Основные логические операции (функции)Инверсия (логическое отрицание)Конъюнкция (логическое
- 14. Основные логические операцииУ каждой функции существует таблица
- 15. Логическая операция ИНВЕРСИЯ(отрицание)Соответствует частице НЕ (NOT)Обозначается А
- 16. Примеры: Сформулируйте отрицания следующих высказываний и укажите значения
- 17. Логическая операция КОНЪЮНКЦИЯ(логическое умножение)Ставит в соответствие каждым
- 18. Примеры:Определить значения истинности следующих высказываний:Ленинград расположен на
- 19. Соответствует союзу ИЛИ (OR)Обозначается ۷ или ●Логическая
- 20. Примеры:Определить значения истинности следующих высказываний:7 – простое
- 21. Логическая операция ИМПЛИКАЦИЯ(логическое следование IMP)Соответствует обороту
- 22. Примеры: Определить значения истинности следующих высказываний:Если 12 делится
- 23. Логическая операция ЭКВИВАЛЕНЦИЯ(равнозначность EQV )Ставит
- 24. Примеры: Определить значения истинности следующих высказываний:12 делится на
- 25. Сложение по модулю 2 (неравнозначность, отрицание однозначности,
- 26. Таблица истинности основных функций
- 27. Плюсы математической логикиПрименяется для описания работы так
- 28. Некоторые функции проводимости F(x), для х-переключательных схем
- 29. Условно-графические обозначения (УГО) некоторых логических элементов
- 30. Схема, реализующая функцию суммы одноразрядного сумматора
- 31. Схема, реализующая функцию переноса одноразрядного сумматора
- 32. Схемотехническая реализация логических элементов Каждый логический элемент – это электронно-техническое изделие.
- 33. Условно-графические обозначения (УГО) некоторых логических элементов
- 34. Условно-графические обозначения (УГО) некоторых логических элементов
- 35. Функциональные схемы и структурные формулы логических устройствОпределите структурную формулу по заданной функциональной схемеXY1F ( X, Y)Ответ:
- 36. Начерти переключательную схему, реализующую
- 37. Скачать презентацию
- 38. Похожие презентации
Логика – это наука о законах и формах мышления. Она изучает абстрактное мышление как средство познания объективного мира. Термин «логика» происходит от древнегреческого logos – «слово, мысль, понятие, рассуждение, закон».
Слайд 2 Логика – это наука о законах и формах
Слайд 3 Логика является одной из дисциплин, образующих математический фундамент
информатики.
Любой язык программирования содержит логические переменные и средства для
описания и вычисления логических выражений.Логические методы применяются и при работе с базами данных.
Зачем нужно изучать ЛОГИКУ?
Слайд 4 В вычислительной технике и автоматике используются логические схемы
– устройства, которые преобразуют двоичные сигналы. Например, полусумматоры и
сумматоры в процессоре.Анализ и проектирование логических схем опираются на законы алгебры логики.
Слайд 5
Этапы развития логики
Первые учения о формах и способах
рассуждений возникли в странах Дальнего Востока (Китай, Индия), но
в основе современной логики лежат учения, созданные древнегреческими мыслителями. Основы формальной логики заложил Аристотель (384–322 гг. до н.э.), который впервые отделил логические формы речи от ее содержания.Слайд 6 В XVII веке немецкий ученый и философ Готфрид
Вильгельм Лейбниц (1646 – 1716) попытался построить первые логические
исчисления, усовершенствовал и уточнил логические символы. На фундаменте, заложенном Лейбницем, другой великий математик, англичанин Джордж Буль (1815-1864) воздвиг здание новой области науки – математической логики.
Начальный раздел математической логики называют алгеброй логики или Булевой алгеброй.
Слайд 7
Алгебра логики
С точки зрения устройства ЭВМ нас интересует
алгебра логики, в которой не рассматривается конкретное содержание основного
понятия логики – высказывания, а важно только истинно оно или ложно.Основным объектом в логике является высказывание.
Слайд 8
Примеры:
Москва – столица России
Студент математического факультета педагогического университета
Треугольник
АВС подобен треугольнику А’В’С’
Луна есть спутник Марса
Кислород – газ
Каша
– вкусное блюдоМатематика – интересный предмет
Железо тяжелее свинца
Треугольник называется равносторонним, если все его стороны равны
Сегодня плохая погода
Река Ангара впадает в озеро Байкал
Какие из этих предложений являются высказываниями?
Ответ: 1, 4, 5, 8, 9, 11
Слайд 9
Основные понятия логики:
Утверждение – высказывание, которое требуется доказать
или опровергнуть.
Например: «Сумма внутренних углов треугольника равна 1800»
Рассуждение –
цепочка высказываний или утверждений, определенным образом связанных друг с другом.Например: «Если хотите начать работать на компьютере, то необходимо сначала включить электропитание»
Умозаключение – логическая операция, в результате которой из одного или нескольких данных высказываний получается (выводится) новое высказывание.
Например: «Все металлы электропроводны». «Ртуть является металлом». Путем умозаключения можно сделать вывод, что «Ртуть электропроводна».
Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты).
Например: (А ۸ (В ۷ С))
Слайд 10
Простые высказывания обозначают
заглавными латинскими буквами
A, B,
C…X, Y, Z и называют
логическими переменными
Значения высказываний
ИСТИНА или
ЛОЖЬ обозначаютсоответственно цифрами 1 и 0
и называют логическими величинами
Составные высказывания называются
логическими выражениями и включают
в себя логические переменные,
операции логики и скобки для изменения
порядка действий операций
Слайд 11
Примеры:
Рассмотрим следующие высказывания:
A = (7 > 3)
B =
(7 = 3)
C = (7 ≠ 3)
D = (B
۸ C) = ((7 = 3) ۸ (7 ≠ 3))На языке алгебры логики эти высказывания можно записать так:
A = ИСТИНА = 1
B = ЛОЖЬ = 0
C = ИСТИНА = 1
D = ЛОЖЬ = 0
Слайд 12
Основная идея математической логики –
в математической
логике надо иметь дело не с конкретным (смысловым) значением
высказывания, а с высказыванием как с абстрактным объектом, не имеющим конкретного содержания.Вследствие этого высказывания теряют особенности предложений естественного языка и приобретают алгебраический вид и могут исчисляться алгеброй логики.
Слайд 13
Основные логические операции (функции)
Инверсия (логическое отрицание)
Конъюнкция (логическое умножение)
Дизъюнкция
(логическое сложение)
Импликация (логическое следование)
Эквиваленция (логическая равнозначность)
Отрицание равнозначности (сложение по
модулю 2)У каждой функции существует таблица истинности.
Всего для двух переменных А и В существует 16 различных логических функций.
Слайд 14
Основные логические операции
У каждой функции существует таблица истинности.
Всего
для двух переменных А и В существует 16 различных
логических функций.
Слайд 15
Логическая операция ИНВЕРСИЯ
(отрицание)
Соответствует частице НЕ (NOT)
Обозначается А или
¬А
Каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся
в том, что исходное высказывание отрицает.
Слайд 16
Примеры:
Сформулируйте отрицания следующих высказываний и укажите значения истинности
полученных отрицаний:
Волга впадает в Каспийское море.
Число 28 не делится
на число 7.6 > 3.
4 ≤ 5.
Ответ: истинными высказываниями являются: 2
Слайд 17
Логическая операция КОНЪЮНКЦИЯ
(логическое умножение)
Ставит в соответствие каждым двум
простым высказываниям составное высказывание, являющееся истинным тогда и только
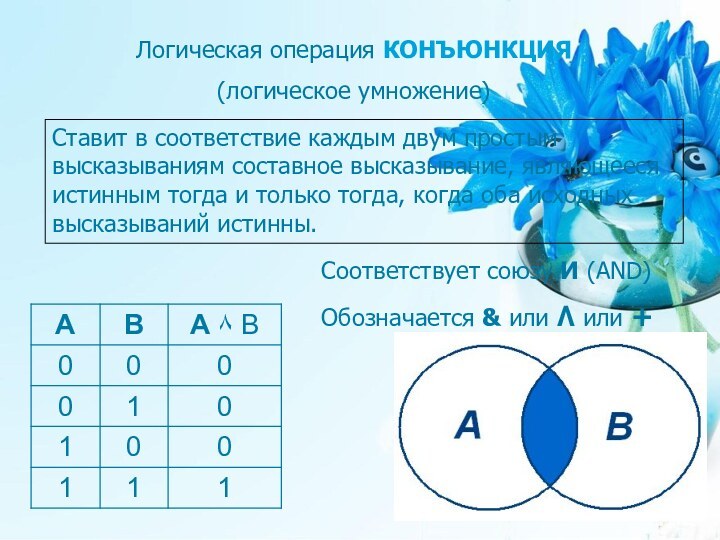
тогда, когда оба исходных высказываний истинны.Соответствует союзу И (AND)
Обозначается & или ۸ или +
Слайд 18
Примеры:
Определить значения истинности следующих высказываний:
Ленинград расположен на Неве
и 2 + 3 = 5
7 – простое число
и 9 – простое число2 * 2 = 4 и 2 * 2 ≤ 5 и 2 * 2 ≥ 4
Москва – столица России и Екатеринбург – столица Сибири
Книга – источник информации и 5 не больше 8
Девочки обычно любят играть в куклы и Не любая машина - автомобиль
Все гуси – птицы и Все игрушки - машины
Ответ: истинными высказываниями являются: 1, 3, 5, 6
Слайд 19
Соответствует союзу ИЛИ (OR)
Обозначается ۷ или ●
Логическая операция
ДИЗЪЮНКЦИЯ
(логическое сложение)
Каждым двум простым высказываниям ставит в соответствие составное
высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, а истинным, когда хотя бы одно из двух исходных высказываний истинно.
Слайд 20
Примеры:
Определить значения истинности следующих высказываний:
7 – простое число
или 9 – простое число
Число 2 четное или Это
простое число2 * 2 = 4 или Белые медведи живут в Африке
Каша – вкусное блюдо или Математика – интересный предмет
Луна – спутник Марса или Луна – спутник Земли
Сегодня плохая погода или Кислород – вода
Microsoft Word – текстовый редактор или Paint – графический редактор
Ответ: истинными высказываниями являются: 1, 2, 3, 5, 7
Слайд 21
Логическая операция ИМПЛИКАЦИЯ
(логическое следование IMP)
Соответствует обороту ЕСЛИ…,
ТО…
Обозначается =>
Ставит в соответствие каждым двум простым высказываниям
составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
Слайд 22
Примеры:
Определить значения истинности следующих высказываний:
Если 12 делится на
6, то 12 делится на 3.
Если 11 делится на
6, то 11 делится на 3.Если 15 делится на 6, то 15 делится на 3.
Если 15 делится на 3, то 15 делится на 6.
Если Мытищи расположены на Неве, то белые медведи обитают в Африке.
Ответ: истинными высказываниями являются: 1, 2, 3, 5
Слайд 23
Логическая операция ЭКВИВАЛЕНЦИЯ
(равнозначность EQV )
Ставит в
соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным
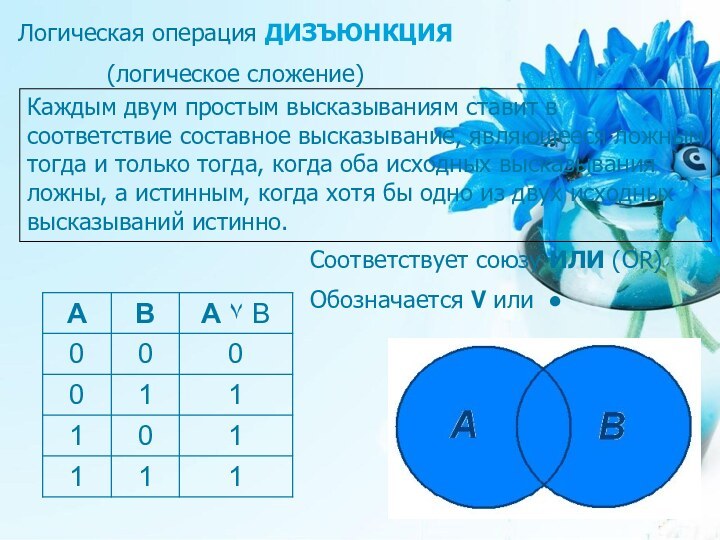
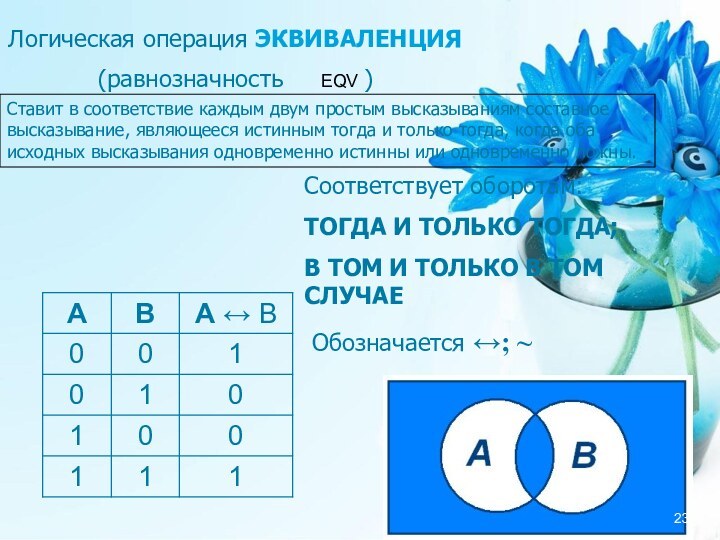
тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.Соответствует оборотам:
ТОГДА И ТОЛЬКО ТОГДА;
В ТОМ И ТОЛЬКО В ТОМ СЛУЧАЕ
Обозначается ↔; ~
Слайд 24
Примеры:
Определить значения истинности следующих высказываний:
12 делится на 6
тогда и только тогда, когда 12 делится на 3.
11
делится на 6 тогда и только тогда, когда 11 делится на 3.15 делится на 6 тогда и только тогда, когда 15 делится на 3.
15 делится на 5 тогда и только тогда, когда 15 делится на 4.
Ответ: истинными высказываниями являются: 1, 2
Слайд 25 Сложение по модулю 2 (неравнозначность, отрицание однозначности, исключающее
ИЛИ)
F=A⊕ B, F=А XOR В
Если a =
011001012b = 001010012
то a ⊕b = 010011002
Слайд 27
Плюсы математической логики
Применяется для описания работы так называемых
дискретных устройств, к числу которых принадлежит целый класс устройств
автоматики и вычислительной техники.При помощи алгебры логики можно производить синтез и анализ электронных схем.
Слайд 32
Схемотехническая реализация логических элементов
Каждый логический элемент –
это электронно-техническое изделие.
Слайд 35
Функциональные схемы и структурные формулы логических устройств
Определите структурную
