- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ОСНОВЫ ЛОГИКИ И ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ КОМПЬЮТЕРА
Содержание
- 2. Процессор
- 3. Логика - это наука о
- 4. Первые учения о формах и способах рассуждений
- 5. Алгебру логики так же называют алгеброй
- 6. Понятие – это форма мышления, фиксирующая основные,
- 7. Высказывание (суждение) – это форма мышления, в
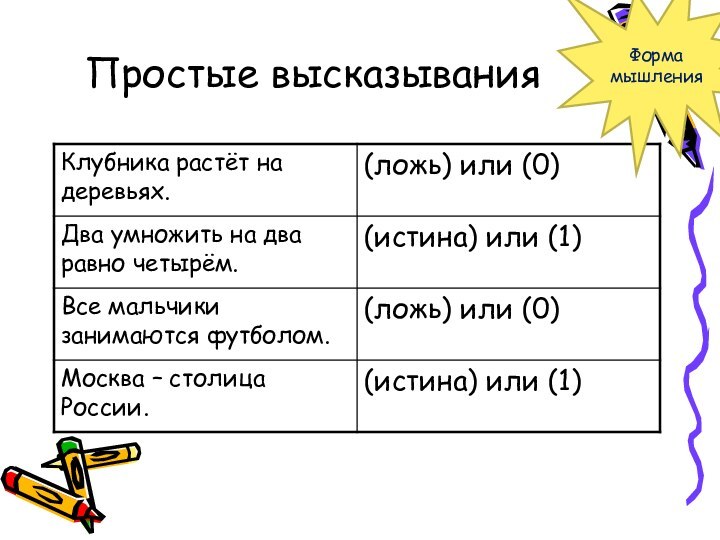
- 8. Простые высказыванияФорма мышления
- 9. Простое высказывание состоит из одного высказывания и
- 10. Сложные высказывания.Форма мышления
- 11. ПредикатыВысказывание состоит из понятий, и его можно
- 12. Умозаключение - это форма мышления, с
- 13. В качестве основных логических операций в составных
- 14. Все операции алгебры логики определяются таблицами истинности.
- 15. Операция НЕ- логическое отрицание (инверсия)Логическая операция НЕ
- 16. Логический элемент инверсия
- 17. Операция ИЛИ – логическое сложение (дизъюнкция нестрогая,
- 18. Логический элемент дизъюнкция
- 19. Операция ИЛИ – логическое сложение (дизъюнкция строгая)Обозначения операции: А xor В, А ∨· В.
- 20. Операция И – логическое умножение (конъюнкция)Выполняет функцию
- 21. Логический элемент конъюнкция
- 22. Операция «ЕСЛИ – ТО» - логическое следование
- 23. Логический элемент импликацияА
- 24. Операция «А тогда и только тогда, когда
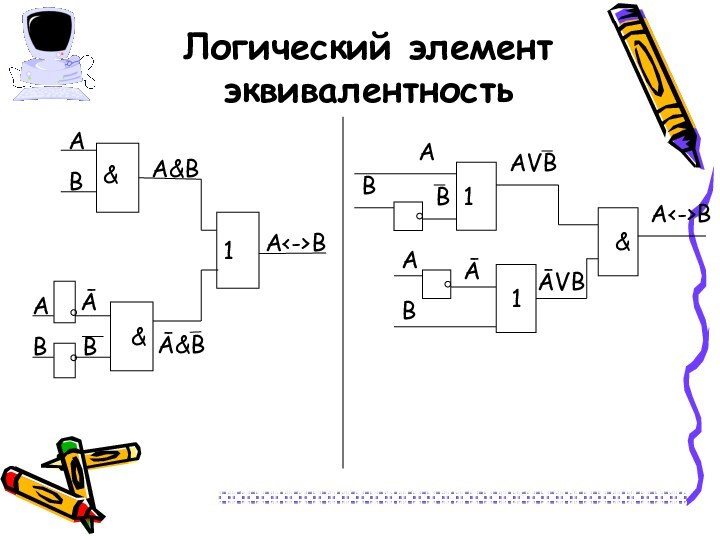
- 25. Логический элемент эквивалентностьАВ
- 26. Каждое составное высказывание можно выразить в виде
- 27. Приоритет логических высказыванийдействия в скобкахинверсия конъюнкция дизъюнкцияимпликация
- 28. МинипрактикумДаны простые высказывания:A={Процессор – устройство для обработки
- 29. Правильные ответы(AVB) (C&D) = 0 (A&B) ->
- 30. Ответ: Всегда ЛОЖНОМинипрактикумКакое значение будет на выходе
- 31. Практическая работа ПКСоздание в электронных таблицах Microsoft Excel(OpenOffice.org Calc) таблиц истинности логических функций:КонъюнкцииДизъюнкцииИнверсииИмпликацииЭквивалентности
- 32. Составление таблиц истинности по логической формулеКоличество строк
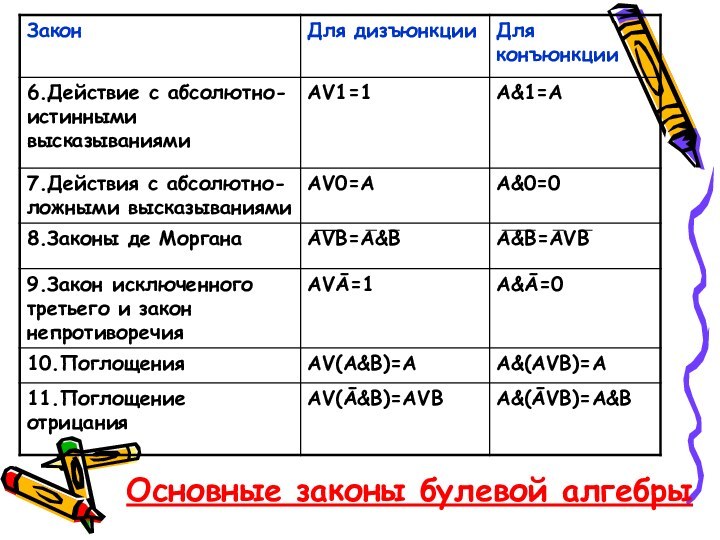
- 33. Основные законы булевой алгебры
- 34. Основные законы булевой алгебры
- 35. Формула склеивания(А В) (А В)=А(А В) (А В)=А
- 36. Формулы поглощенияА (А В)= АА
- 37. Тестовое заданиеНачать тест
- 38. Вопросы и задания по теме «Основы логики»Зачёт по теме «Основы логики»
- 39. Скачать презентацию
- 40. Похожие презентации
Процессор компьютера выполняет арифметические и логические операции над двоичными кодами. И поэтому чтобы иметь представление об устройстве компьютера, необходимо познакомиться с основными логическими элементами, лежащими в основе его построения. Для
Слайд 3 Логика - это наука о формах и способах
мышления. Термин «логика» происходит от древнегреческого logos, означающего «слово, мысль,
понятие, рассуждение, закон»Основными формами мышления являются понятие, высказывание и умозаключение.
Слайд 4 Первые учения о формах и способах рассуждений возникли
в странах Дальнего Востока (Китай, Индия), но в основе
современной логики лежат учения, созданные древнегреческими мыслителями. Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления от его содержания.Слайд 5 Алгебру логики так же называют алгеброй Буля, или
булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего
в XIX веке ее основные положения.Слайд 6 Понятие – это форма мышления, фиксирующая основные, существенные
признаки объекта.
Понятие имеет две стороны: содержание и объём.
Например, содержание понятия «персональный компьютер – это универсальное электронное устройство для автоматической обработки информации, предназначенное для одного пользователя.»Объём понятия «персональный компьютер» выражает всю совокупность существующих в настоящее время в мире персональных компьютеров.
Форма мышления
Слайд 7 Высказывание (суждение) – это форма мышления, в которой
что-либо утверждается или отрицается о свойствах реальных предметов, их
свойствах и отношениях между ними.
Высказывание могут принимать только два значения – Истина (обозначается 1) или Ложь (обозначается 0).
Высказывания могут быть простыми и составными.
Форма мышления
Слайд 9 Простое высказывание состоит из одного высказывания и не
содержит логической операции. Составное высказывание содержит высказывания, объединенные логическими
операциями.Например, высказывание «Процессор является устройством обработки информации и принтер является устройством печати» является составным высказыванием, состоящим из двух простых, соединённых союзом «и».
Слайд 11
Предикаты
Высказывание состоит из понятий, и его можно сравнить
с арифметическим выражением. В математической логике рассматриваются предикаты, т.
е. функциональные зависимости от неопределённых понятий (терминов), которые можно сравнить с переменными в уравнении.В предикатах 1 порядка один из терминов является неопределённым понятием: «X – человек».
В предикатах 2 порядка два термина неопределённы: «X любит Y».
В предикатах 3 порядка неопределённы три термина: «Z – сын X и Y».
Преобразуем в высказывания:
«Сократ – человек»;
«Ксантиппа любит Сократа»;
«Софрониск – сын Сократа и Ксантиппы»
Слайд 12 Умозаключение - это форма мышления, с помощью которой
из одного или нескольких высказываний может быть получено новое
высказывание.Форма мышления
Например, если мы имеем высказывание «Все углы треугольника равны», то мы можем путём умозаключения доказать, что в этом случае справедливо высказывание «Это треугольник равносторонний».
Слайд 13 В качестве основных логических операций в составных высказываниях
используются:
НЕ (логическое отрицание, инверсия)
ИЛИ (логическое сложение, дизъюнкция)
И (логическое умножение,
конъюнкция)Операция «ЕСЛИ - ТО» (логическое следование, импликация)
Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)
Слайд 14 Все операции алгебры логики определяются таблицами истинности. Таблица
истинности определяет результат выполнения операции для всех возможных логических
значений исходных высказываний.Простые высказывания в алгебре логики обозначаются прописными латинскими буквами:
A, B, C, D …
Слайд 15
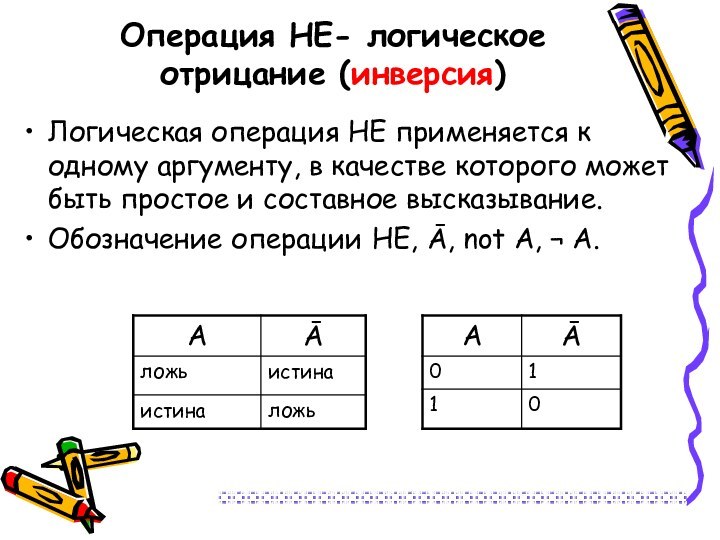
Операция НЕ- логическое отрицание (инверсия)
Логическая операция НЕ применяется
к одному аргументу, в качестве которого может быть простое
и составное высказывание.Обозначение операции НЕ, Ā, not А, ¬ А.
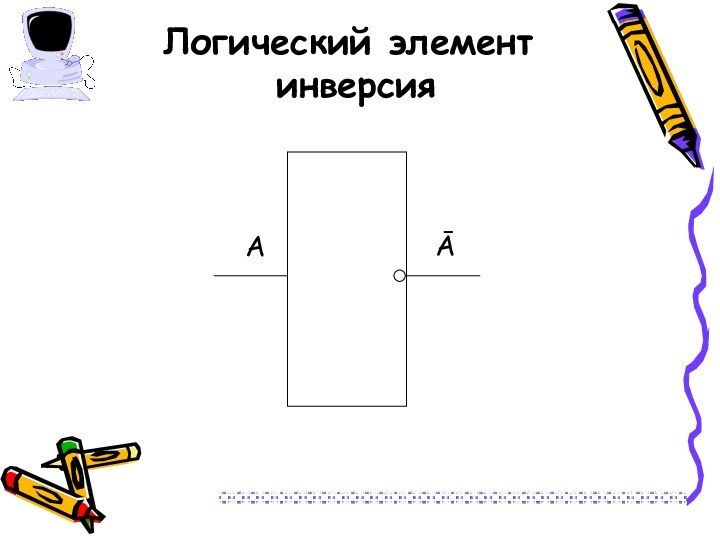
Слайд 17
Операция ИЛИ – логическое сложение (дизъюнкция нестрогая, объединение)
Выполняет
функцию объединения двух высказываний, в качестве которых может быть
и простое, и составное высказывание.Обозначения операции: А или В, А or В, А V В.
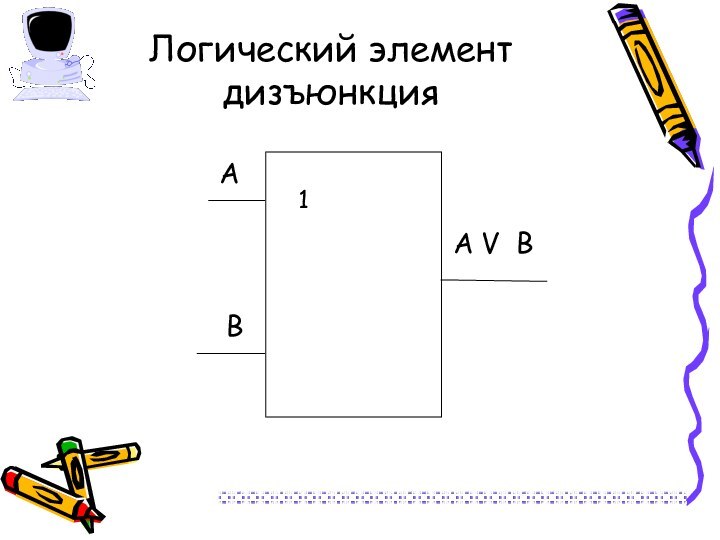
Слайд 19
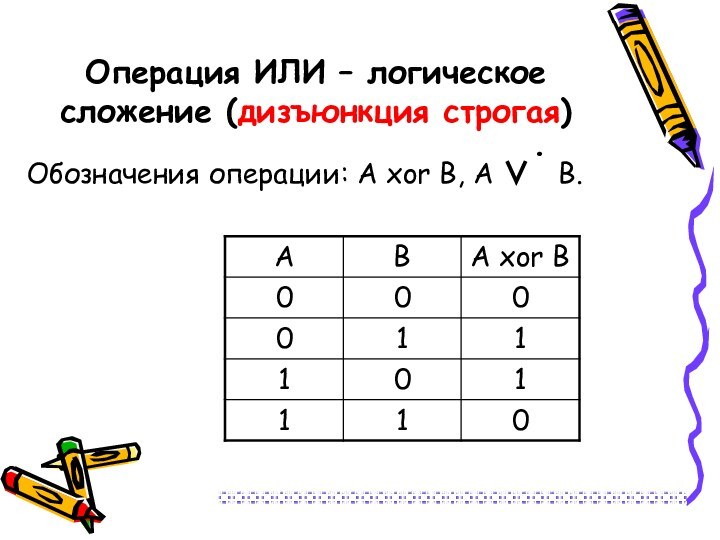
Операция ИЛИ – логическое сложение (дизъюнкция строгая)
Обозначения операции:
А xor В, А ∨· В.
Слайд 20
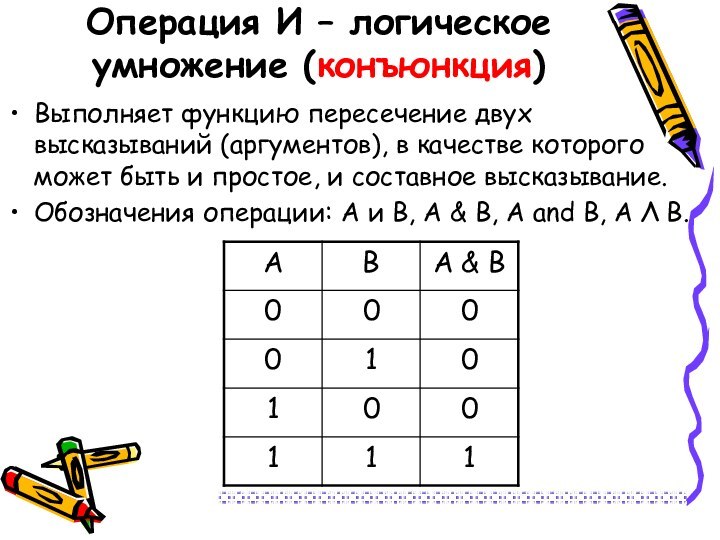
Операция И – логическое умножение (конъюнкция)
Выполняет функцию пересечение
двух высказываний (аргументов), в качестве которого может быть и
простое, и составное высказывание.Обозначения операции: А и В, А & В, А and В, А Λ В.
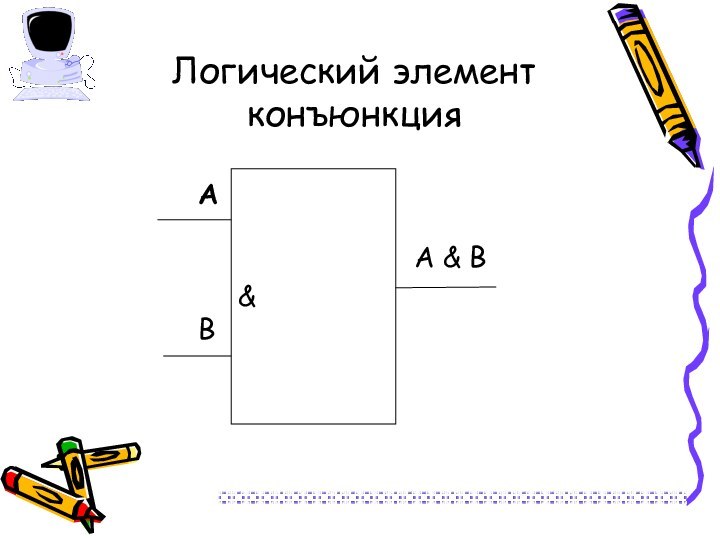
Слайд 22
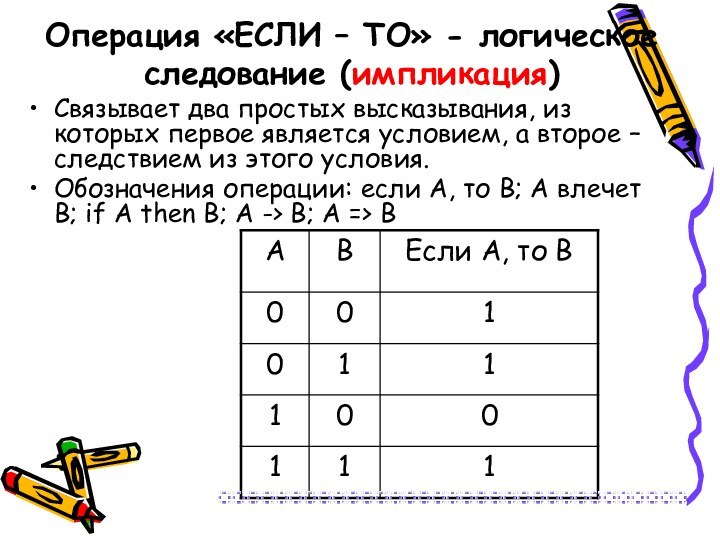
Операция «ЕСЛИ – ТО» - логическое следование (импликация)
Связывает
два простых высказывания, из которых первое является условием, а
второе – следствием из этого условия.Обозначения операции: если А, то В; А влечет В; if A then B; А -> В; А => В
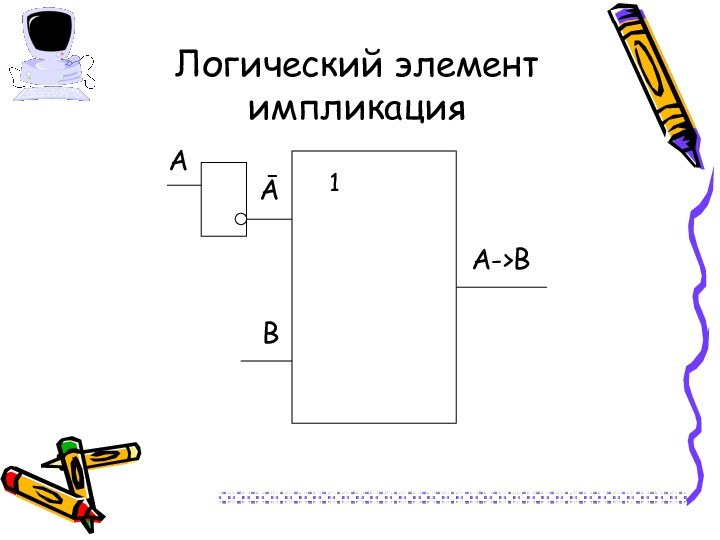
Слайд 24 Операция «А тогда и только тогда, когда В»
(эквивалентность, равнозначность)
Обозначения операции: А ~ В, А В,
А Ξ ВРезультат операции эквивалентность истинен тогда и только тогда, когда А и В одновременно истины или ложны.
Слайд 26 Каждое составное высказывание можно выразить в виде формулы
(логического выражения).
Логическое выражение(формула) – содержит логические переменные, обозначающие высказывания,
соединённые знаками логических операций.
Слайд 27
Приоритет логических высказываний
действия в скобках
инверсия
конъюнкция
дизъюнкция
импликация
эквивалентность
Пример:
U
∨ (В ⇒ С) & D ⇔ Ū
Порядок вычисления:
1)
Ū2) (В ⇒ С)
3) (В ⇒ С) & D
4) U ∨ (В ⇒ С) & D
5) U ∨ В ⇒ С & D ⇔ Ū
Слайд 28
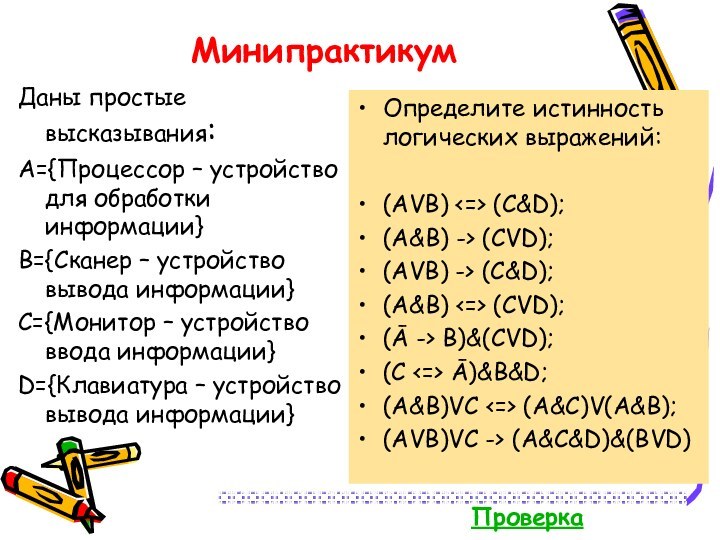
Минипрактикум
Даны простые высказывания:
A={Процессор – устройство для обработки информации}
B={Сканер
– устройство вывода информации}
C={Монитор – устройство ввода информации}
D={Клавиатура –
устройство вывода информации}Определите истинность логических выражений:
(AVB) <=> (C&D);
(A&B) -> (CVD);
(AVB) -> (C&D);
(A&B) <=> (CVD);
(Ā -> B)&(CVD);
(C <=> Ā)&B&D;
(A&B)VC <=> (A&C)V(A&B);
(AVB)VC -> (A&C&D)&(BVD)
Проверка
Слайд 29
Правильные ответы
(AVB) (C&D) = 0
(A&B) ->
(CVD) = 1
(AVB) -> (C&D) = 0
(A&B) (CVD)
= 1(Ā -> B)&(CVD) = 0
(C <=> Ā)&B&D = 0
(A&B)VC <=> (A&C)V(A&B) = 1
(AVB)VC -> (A&C&D)&(BVD) = 0
A=1
B=0
C=0
D=0
Назад
Слайд 30
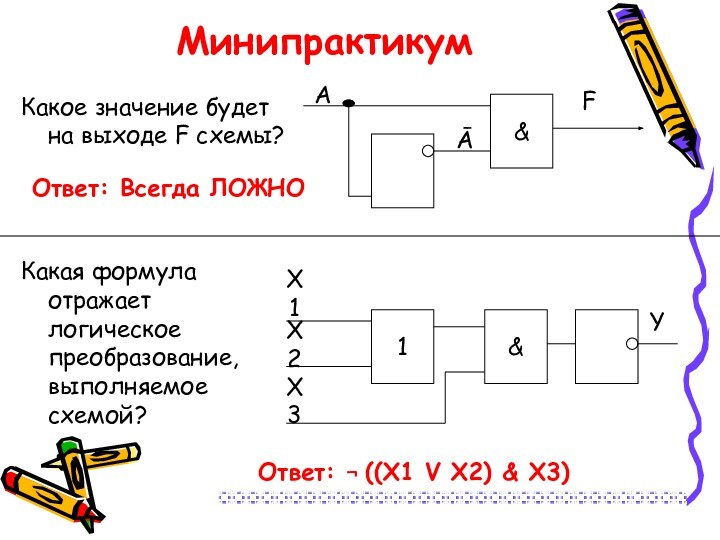
Ответ: Всегда ЛОЖНО
Минипрактикум
Какое значение будет на выходе F
схемы?
Какая формула отражает логическое преобразование, выполняемое схемой?
Ответ: ¬ ((X1
V X2) & X3)
Слайд 31
Практическая работа ПК
Создание в электронных таблицах Microsoft Excel(OpenOffice.org
Calc) таблиц истинности логических функций:
Конъюнкции
Дизъюнкции
Инверсии
Импликации
Эквивалентности
Слайд 32
Составление таблиц истинности по логической формуле
Количество строк -
2ⁿ, где n- это количество логических переменных
Количество столбцов -
количество логических переменных + количество логических операций.Пример: Ā&В
Количество строк = 22 = 4
Количество столбцов = 2 + 2 = 4
