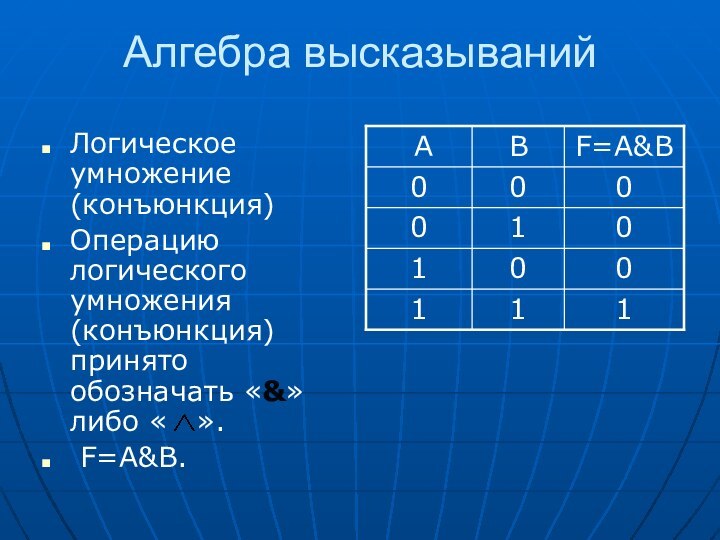
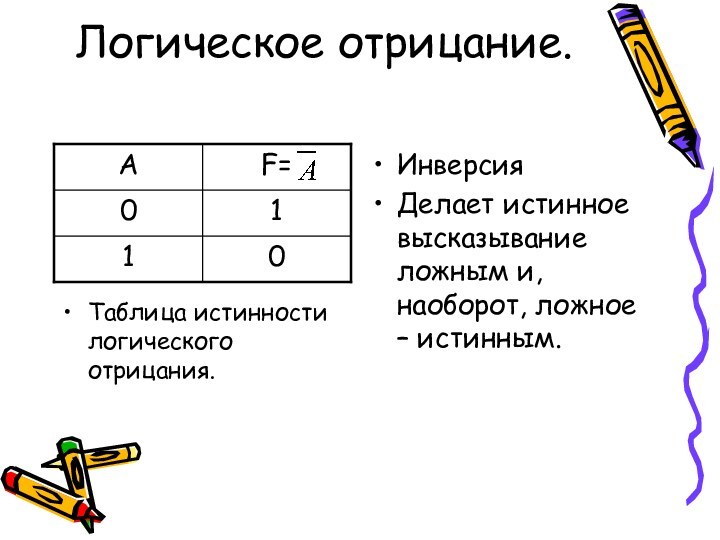
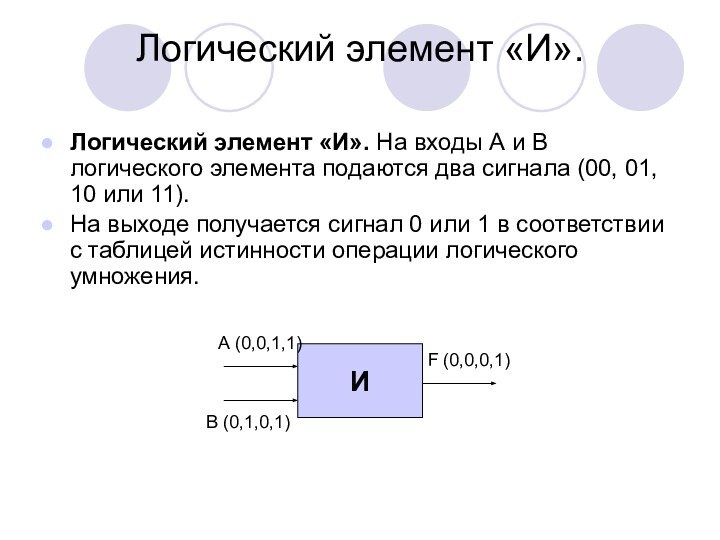
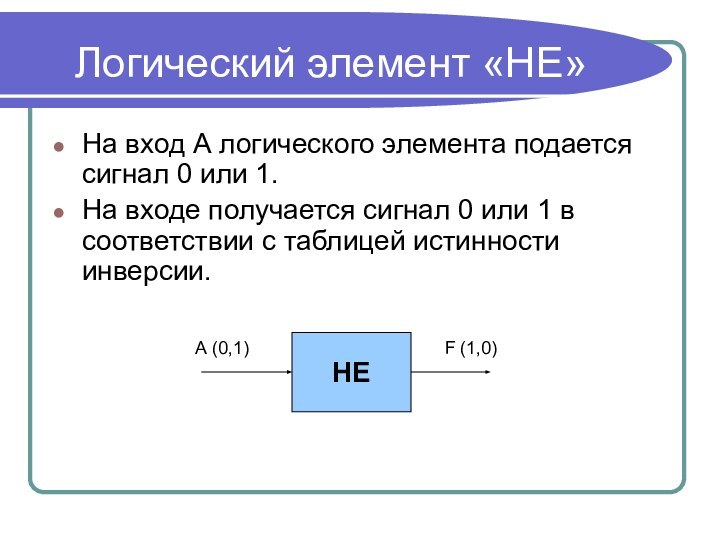
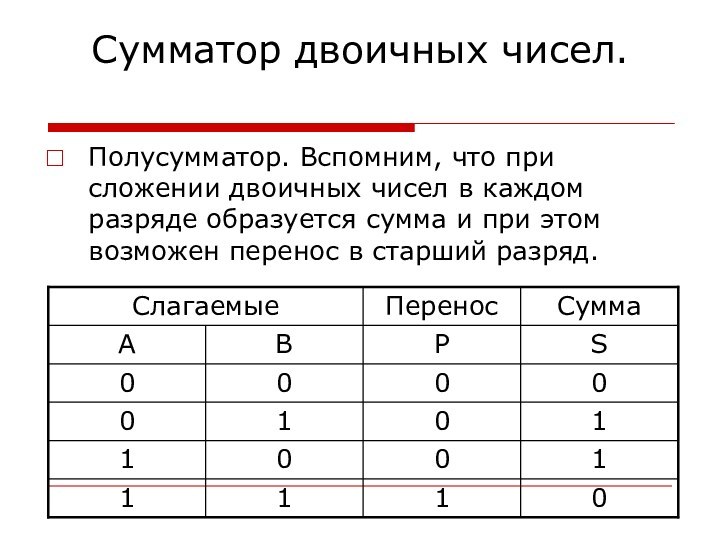
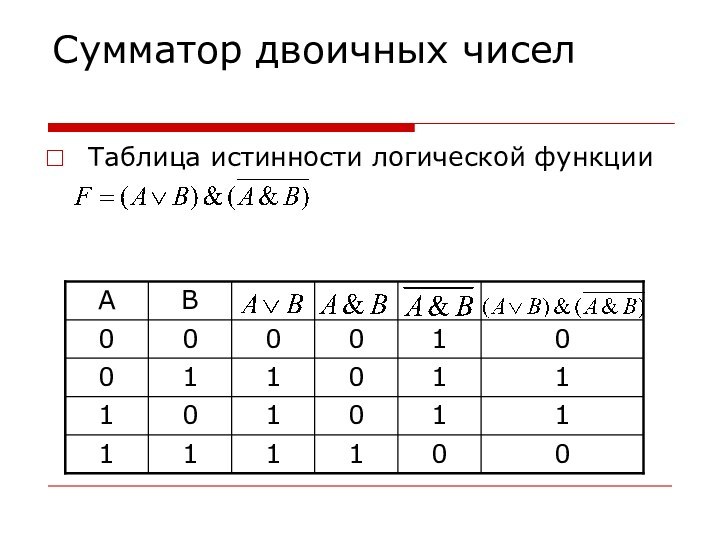
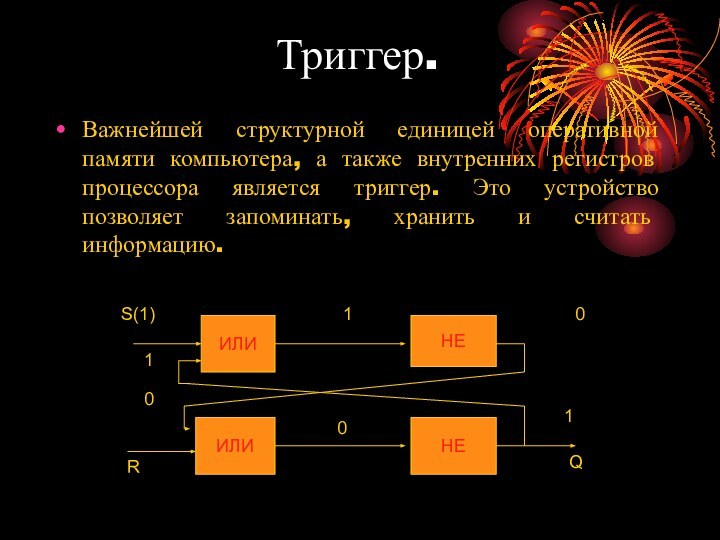
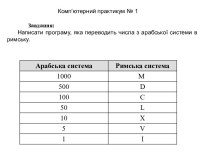
форма мышления.
Понятие - это форма мышления, фиксирующая основные, существенные
признаки объекта.Высказывание – форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинно, либо ложно.