Презентация на тему Основы моделирования

взаимосвязанную совокупность положений, определений, методов и средств создания и

изучения моделей. Эти положения, определения, методы и средства, как и сами модели, являются предметом теории моделирования.
Основная задача теории моделирования заключается в том, чтобы вооружить исследователей технологией создания таких моделей, которые достаточно точно и полно фиксируют интересующие свойства оригиналов, проще или быстрее поддаются исследованию и допускают перенесение его результатов на оригиналы.

объекта (оригинала) другим (моделью) и фиксация или изучение свойств

оригинала путем исследования свойств модели.
Объект (система) определяется совокупностью параметров и характеристик.
Множество параметров системы отражает ее внутреннее содержание – структуру и принципы функционирования.
Характеристики системы – это ее внешние свойства, которые важны при взаимодействии с другими системами. Характеристики системы находятся в функциональной зависимости от ее параметров.

физическая или абстрактная система, адекватно представляющая объект исследования.

Модель может быть представлена в различных формах :
1) образец для массового изготовления изделия;
2) приспособление для получения отпечатка в литейной форме.
3) изделие, с которого снимается форма (шаблоны, лекала);
4) изображаемый художником человек или предмет;
5) устройство, воспроизводящее строение или действие какого-либо другого устройства;
6) любой образ объекта, процесса или явления, используемый в качестве представителя оригинала (изображение, схема, чертеж, карта);
7) математический аппарат, описывающий объект, процесс или явление;

моделей
Свойства моделей

2. Аналоговое моделирование.

3. Полунатурное моделирование.

4. Математическое моделирование.

5. Компьютерное моделирование.

старых видов моделирования. Чтобы качественно или количественно изучить поведение

объекта изготавливали его модель в масштабе уменьшения или увеличения, на которой проводились исследования. Например, при изучении водослива гидротехнической плотины ее размеры при переходе к модели уменьшаются линейно, но масса падающей воды уменьшается в кубе масштаба. Для получения адекватных результатов возникает необходимость выработки критериев подобия, определяющих правила моделирования по определяющему параметру.
Данный вид моделирования по другому называют физическим моделированием.

одними и теми же уравнениями, то можно одно из

явлений выбрать за основу для модели, а остальные выражать через него. Модельным выбирается то явление или процесс, в котором можно легче и точнее произвести измерения.
Так как лучше всего разработаны измерения электрических величин, то и модели стараются выполнить на электрических схемах. Этот вид моделирования принято называть электро-моделированием. Оно широко применялось в 50 – 60 годах ХХ века. Развитие данного вида моделирования привело к созданию аналоговых вычислительных машин (АВМ).
При моделировании на АВМ задача сводится к нахождению такого электрического контура, который адекватно отображает моделируемый процесс. Проще всего на АВМ моделируются процессы, требующие решения дифференциальных уравнений, интегрирования или дифференцирования.

строятся в основном на базе операционных усилителей постоянного тока

с большим коэффициентом усиления в разомкнутом состоянии и глубокой отрицательной обратной связью. В зависи-мости от структуры и характера входной цепи и цепи обратной связи операционный усилитель выполняет линейную или нелинейную математическую операцию или комбинацию этих операций. Результирующая погрешность результатов, полученных на АВМ, зависит от неидеальности работы отдельных решающих элементов, неточности установки их коэффициентов передачи и начальных условий, от характера и особенностей решаемой задачи. Практически погрешность не превышает нескольких %.

Польский электронный аналоговый компьютер «AKAT-1».

комплекс мероприятий, который предназначен для исследования поведения объекта в

условиях близких к реальным.
Отличие полунатурных испытаний от натурных заключается в том, что на объект оказываются не реальные воздействия, а моделируемые, формируемые искусственно.
Достоверность результатов моделирования в значительной мере определяется достоверностью формируемых воздействий. Очевидно, что достоверность полунатурного моделирования ниже, чем при испытаниях в реальных условиях - это недостаток полунатурных испытаний.
Достоинством данного вида моделирования является несоизмеримо меньшие, чем при натурных испытаниях затраты и большое разнообразие моделируемых ситуаций. Есть реальная возможность смоделировать ситуации, которые редко встречаются в жизни и которые могут оказаться чрезвычайно полезны для исследователя.

эффективно применяется при создании бортовых авиационных систем, систем автоматического

и полуавтоматического регулирования или управления.
На основе полунатурного моделирования создаются различные тренажеры. Их использование - единственный путь избежать больших затрат и возможных негативных результатов в ходе подготовки будущих пилотов, водителей и т.д.

тех случаях, когда весь моделируемый процесс удается представить в

форме математических уравнений и отношений, которые исследуются с использованием ЭВМ.
При математическом моделировании экспериментатор сам распоряжается планом проведения исследования: какие параметры и в как надо варьировать, а какие – стабилизировать. Исследование ведется в строгих рамках принятых допущений и веденных в рассмотрение параметров.
При составлении математической модели нужно стремиться оставлять для рассмотрения лишь наиболее существенные параметры, делать математическое описание как можно проще.
Математическая модель в ходе исследования может быть изменена и усовершенствована путем устранения выявленных ее недостатков.

по сравнению с аналоговым являются:
♦ большая

универсальность;
♦ большая точность;
♦ быстрое переключение с одной задачи на другую.

К недостаткам следует отнести:
♦ сложности программирования;
♦ трудность соблюдения натурального масштаба времени.

При математическом моделировании всегда возникает важная проблема, связанная с однозначным соответствием идеализированной модели и реального объекта. Для создания математической модели, достаточно точно отражающей сложный натуральный процесс или явление, требуется глубокое понимание натурального процесса и хорошая инженерная интуиция.

модели с помощью компьютера.
В отличие

от математической компьютерная модель имеет две составляющие:
– программную, изменяемую при переходе к новой модели;
– аппаратную, остающуюся неизменной.
Программная составляющая является абстрактной математической моделью специального вида, которая интерпретируется процессором компьютера и «выполняется».
Компьютерная модель при наличии соответствующих аппаратных средств предоставляет возможность наблюдения некоторых физических процессов, например, движение образов на экране, которое воспринимается как поведение модели.
Важной особенностью компьютерного моделирования является его интерактивность, т.е. возможность вмешиваться в процессе моделирования и влиять на получаемые результаты.

моделирующей программы является уже физическим устройством и может выступать

в качестве имитатора реального объекта. При наличии специальных адаптеров компьютерную модель можно «подключать» к другим реальным объектам точно так, как её физические прототипы.
Таким образом, объединяя компьютерные модели с реальными устройствами можно создавать полунатурные модели сложных информационных систем.
Можно выделить следующие этапы развития компьютерного моделирования:
♦ Написание уникальных моделирующих программ на языках программирования («Алгол» и «Фортран»).
♦ Автоматизация моделирования на основе создания библиотек численных методов для заданного класса уравнений.
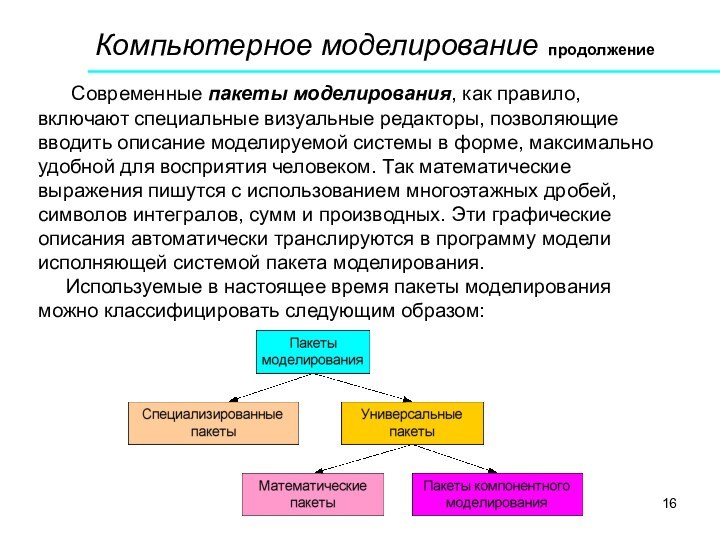
♦ Создание систем автоматизации моделирования (пакеты моделирования).

как правило, включают специальные визуальные редакторы, позволяющие вводить описание

моделируемой системы в форме, максимально удобной для восприятия человеком. Так математические выражения пишутся с использованием многоэтажных дробей, символов интегралов, сумм и производных. Эти графические описания автоматически транслируются в программу модели исполняющей системой пакета моделирования.
Используемые в настоящее время пакеты моделирования можно классифицировать следующим образом:

специфические понятия конкретной прикладной области (химическая технология, теплотехника, электротехника

и т.д.) и имеют узкую область применения.
Универсальные пакеты делятся на математические пакеты и пакеты компонентного моделирования.
Математические пакеты (Mathematics, MATLAB, Maple Mathcad) используются в случаях, когда математическая модель всей моделированной системы уже построена и её требуется только исследовать. Математические пакеты позволяют проводить символьные преобразования модели или решать их численно.
Компонентное моделирование широко используется при проектировании технических объектов. Описание моделируемой системы строится из готовых библиотечных компонентов, а совокупная математическая модель формируется пакетом автоматически. Размерность и сложность совокупной системы уравнений таковы, что для ее решения применяются численные методы.

моделей
Свойства моделей

предполагает выполнение следующих этапов:
1. Формулирование

цели моделирования.
В качестве цели моделирования может быть выбрано: создание объектов с заданными свойствами; определение последствий воздействия на объект и принятие правильного решения; повышение эффективности управления объектом (или процессом).
2. Разработка концептуальной модели.
Концептуальная (содержательная) модель в словесной форме определяет состав и структуру системы, свойства компонентов и причинно-следственные связи между ними.
3. Подготовка исходных данных.
Для количественных параметров необходимо определить их конкретные значения, которые будут использованы в виде исходных данных при моделировании.
4. Разработка математической модели.
Составление формального описания взаимосвязи входных и выходных параметров объектов.

Выбор метода моделирования.
В

зависимости от типа модели могут быть применены аналитические, имитационные или статистические методы ее исследования.
6. Выбор средств моделирования.
Определение состава аппаратных средств (платформа, тип процессора, набор периферийного оборудования) и программного обеспечения (языки программирования, пакеты моделирования).
7. Разработка программной модели.
Написание программы на стандартных языках программирования или использование инструментальных средств пакетов моделирования.
8. Проверка адекватности и корректировка модели.
Применение статистических методов определения степени несоответствия параметров модели и объекта. Изменение модели в случае рассогласования параметров, превышающего допустимые пределы. Определение области применимости модели.

Планирование экспериментов.
Определение значений и последовательности задания

входных управляемых параметров (факторов) для получения достаточного для изучения объекта набора значений выходных характеристик (откликов).
10. Выполнение моделирования на ЭВМ, анализ результатов
моделирования.
Проведение эксперимента в соответствии с разработанным планом, нахождение аналитических зависимостей между факторами и характеристиками, оценка погрешностей полученных результатов.

моделей
Свойства моделей

областей, сфер их применения, бывают трех видов:

Познавательная модель - форма организации и представления знаний, средство соединения новых и старых знаний. Познавательная модель, как правило, подгоняется под реальность и является теоретической моделью.

Прагматическая модель - средство организации практических действий, рабочего представления целей системы для ее управления. Реальность в них подгоняется под некоторую прагматическую модель. Это, как правило, прикладные модели.

Инструментальная модель - средство построения, исследования и/или использования прагматических и/или познавательных моделей.
Познавательные модели отражают существующие, а прагматические - хоть и не существующие, но желаемые и, возможно, исполнимые отношения и связи.

моделирования модели бывают:

♦ эмпирические - на

основе эмпирических фактов, зависимостей;

♦ теоретические - на основе математических описаний;

♦ смешанные, полуэмпирические - на основе эмпирических зависимостей и математических описаний.

участвующих в ее описании, нет временного параметра. Статическая модель

в каждый момент времени дает лишь "фотографию" системы.
Пример. Закон Ньютона F=a*m - это статическая модель движущейся с ускорением «a» материальной точки массой «m». Эта модель не учитывает изменение ускорения от одной точки к другой.

Модель динамическая, если среди ее параметров есть временной параметр, т.е. она отображает систему (процессы в системе) во времени.
Пример. Модель S=gt2/2 - динамическая модель пути при свободном падении тела. Динамическая модель закона Ньютона: F(t)=a(t)m(t). Еще лучшей формой динамической модели Ньютона является F(t)=s″(t)m(t).

Модель дискретная, если она описывает поведение системы только в дискретные моменты времени.
Пример. Если рассматривать только t=0, 1, 2, :, 10 (сек), то модель S(t)=gt2/2 или числовая последовательность S0=0, S1=g/2, S2=2g, S3=9g/2, :, S10=50g может служить дискретной моделью движения свободно падающего тела.

системы для всех моментов времени из некоторого промежутка времени.

Пример. Модель S=gt2/2, 0
Модель имитационная, если она предназначена для испытания или изучения возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели.
Пример. Пусть модель экономической системы производства товаров двух видов 1 и 2, соответственно, в количестве x1 и x2 единиц и стоимостью каждой единицы товара a1 и a2 на предприятии описана в виде соотношения: a1x1+a2x2=S, где S - общая стоимость произведенной предприятием всей продукции (вида 1 и 2). Можно ее использовать в качестве имитационной модели, по которой можно определять (варьировать) общую стоимость S в зависимости от тех или иных значений объемов производимых товаров.

Модель детерминированная, если каждому входному набору воздействий соответствует вполне определенный и однозначно определяемый набор выходных параметров;
Пример. Приведенные выше физические модели - детерминированные.

факторы.
Пример. Если в модели S=gt2/2,

0
Модель функциональная, если она представима в виде системы каких - либо функциональных соотношений.
Пример. Непрерывный, детерминированный закон Ньютона и модель производства товаров (см. выше) - функциональные.

Модель логическая, если она представима логическими функциями.
Пример. Совокупность двух логических функций вида:, , может служить математической моделью одноразрядного сумматора.

Модель алгоритмическая, если она описана некоторым алгоритмом или комплексом алгоритмов, определяющим ее функционирование, развитие.
Пример. Моделью вычисления суммы бесконечного убывающего ряда чисел может служить алгоритм вычисления конечной суммы ряда до некоторой заданной степени точности.

Классификация моделей продолжение

моделей
Свойства моделей

всегда отображает некоторую систему, т.е. имеет цель;

♦ конечность - модель отображает оригинал лишь в конечном числе его отношений и, кроме того, ресурсы моделирования конечны;
♦ упрощенность - модель отображает только существенные стороны объекта и, кроме того, должна быть проста для исследования или воспроизведения;
♦ приблизительность - действительность отображается моделью грубо или приблизительно;
♦ адекватность - модель должна достоверно описывать моделируемую систему;
♦ наглядность, обозримость основных ее свойств и отношений;
♦ доступность и технологичность для исследования или воспроизведения;
♦ полнота - в модели должны быть учтены все основные связи и отношения, необходимые для обеспечения цели моделирования;