Презентация на тему Параметрическое линейное программирование

собой один из разделов математического программирования, изучающий задачи, в

которых целевая функция или ограничения зависят от одного или нескольких параметров.
С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения.

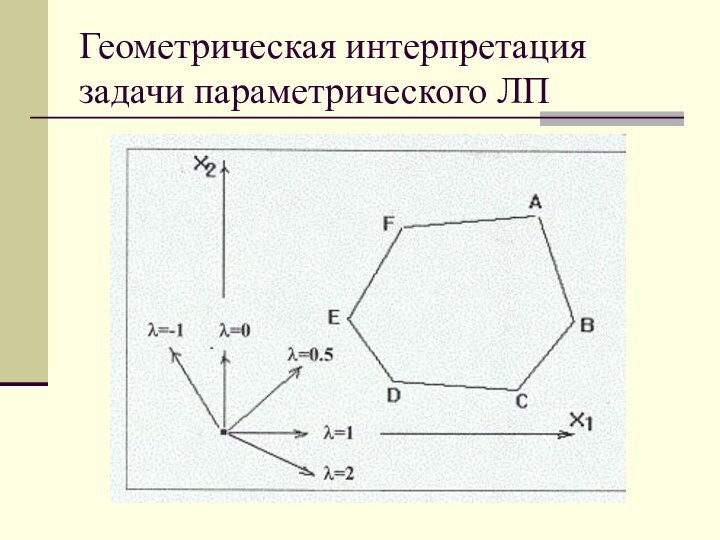
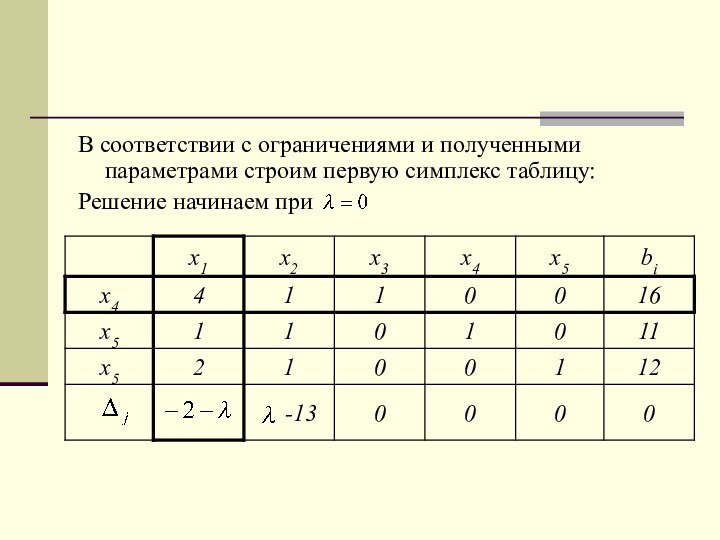
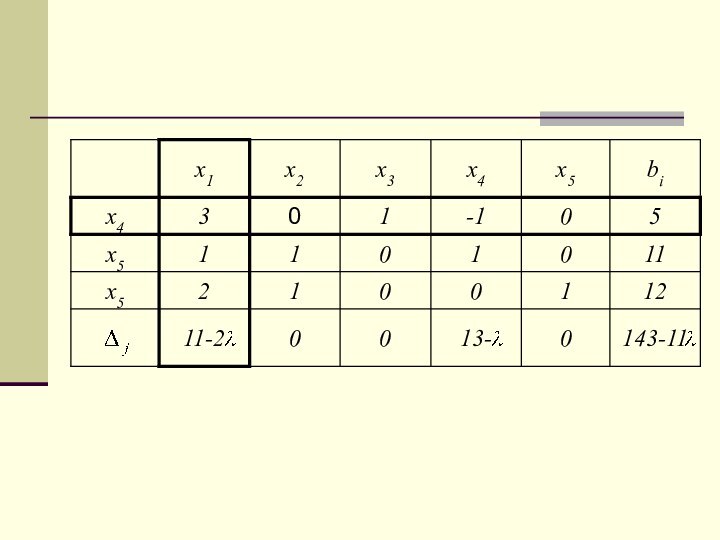
Сущность задачи параметрического ЛП

Если обратиться к геометрической интерпретации задачи, то можно

заметить, что вектор-градиент линейной формы определяется её параметром. Например, для целевой функции L(X, λ) = λX1 + (1-λ)X2 при различных значениях параметра λ градиент определяет различные направления роста функции.
Нетрудно видеть, что, если при некотором значении параметра максимум достигается в вершине A, то небольшая вариация этого значения несколько изменит направление градиента, но не изменит положение точки максимума. Отсюда напрашивается вывод, что некоторый план, оптимальный при λ = λ0 оптимален и в окрестности λ0, т.е. при α ≤ λ ≤ β где λ0   [α, β].

некоторому числу , находим оптимальный план Х* или устанавливаем

неразрешимость полученной задачи линейного программирования.
Определяют множество значений параметра , для которых найденный оптимальный план является оптимальным или задача неразрешима. Эти значения параметра исключаются из рассмотрения.
Полагают значение параметра равным некоторому числу, принадлежавшему оставшейся части промежутка, и находят решение полученной задачи линейного программирования.
Определяют множество значений параметра , для которых новый оптимальный план остается оптимальным или задача неразрешима. Вычисления повторяются до тех пор, пока не будут исследованы все значения параметра .

выпустить два вида продукции А и В, для изготовления

которых используется три вида сырья, нормы расходов заданы в таблице. Известно, что цена на А единицу продукции может изменяться от 2 до 12 у.е., для В от 13 до 3 у.е. Найти оптимальные планы выпуска для заданных интервалов цен.

первую симплекс таблицу:
Решение начинаем при

решение найдено. Найдем интервал изменения , при

котором решение будет оставаться оптимальным.





При > выбранный столбец является разрешающим. Для нахождения нового оптимального решения при >