Слайд 2
Понятие о логике, как науке
Логика – совокупность правил,
которым подчиняется процесс мышления.
Логика – это наука о правилах
рассуждений.
Логика, как наука о законах и формах мышления, изучает абстрактное мышление, как средство познания объективного мира.
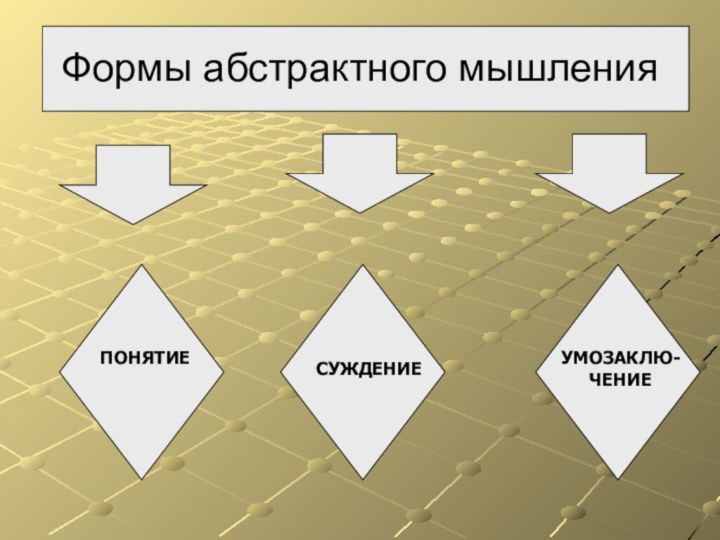
Слайд 3
Формы абстрактного мышления
ПОНЯТИЕ
СУЖДЕНИЕ
УМОЗАКЛЮ-ЧЕНИЕ
Слайд 4
ПОНЯТИЕ
Форма мышления, в которой отражаются существенные признаки отдельного
предмета или класса однородных предметов.
Например: растения, животные, стол, компьютер.
Слайд 5
СУЖДЕНИЕ
Это мысль, в которой что-либо утверждается или отрицается
о предметах.
Суждениями являются истинные или ложные повествовательные предложения.
Пример: Весна
наступила.
Луна – естественный спутник Земли.
Слайд 6
УМОЗАКЛЮЧЕНИЕ
Это прием мышления, когда из исходного знания получается
новое знание.
Например:
Все металлы – простые вещества.
Литий – металл.
Литий –
простое вещество.
Все 10-классники изучают физику.
Анна – десятиклассница.
Анна изучает физику.
Слайд 7
Логика, как наука, подразделяется на:
формальную логику – науку
о законах и формах мышления;
математическую логику – изучающую логические
связи и отношения, лежащие на основе логического вывода.
Слайд 8
Этапы развития логики
1 этап: связан с работами ученого
и философа Аристотеля (384-322 г. до н.э.). Он впервые
дал систематическое изложение логики. Аристотель подверг анализу человеческое мышление, его формы – понятие, суждение, умозаключение. Так возникла формальная логика.
2 этап: появление математической или символьной логики. Основы ее заложил немецкий ученый и философ Готфрид Вильгельм Лейбниц (1646-1716 г.). Он сделал попытку построить первые логические исчисления. Считал, что можно заменить простые рассуждения действиями со знаками и привел соответствующие правила.
Развил эту идею англичанин Джордж Буль (1815-1864). В его работах логика приобрела свой алфавит, орфографию и грамматику.
Слайд 9
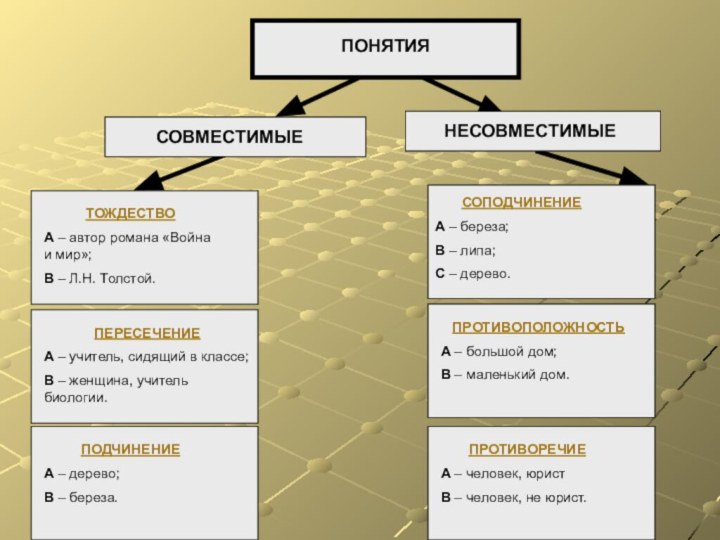
ПОНЯТИЯ
СОВМЕСТИМЫЕ
НЕСОВМЕСТИМЫЕ
ТОЖДЕСТВО
А – автор романа «Война и мир»;
В –
Л.Н. Толстой.
ПЕРЕСЕЧЕНИЕ
А – учитель, сидящий в классе;
В – женщина,
учитель биологии.
ПОДЧИНЕНИЕ
А – дерево;
В – береза.
СОПОДЧИНЕНИЕ
А – береза;
В – липа;
С – дерево.
ПРОТИВОПОЛОЖНОСТЬ
А – большой дом;
В – маленький дом.
ПРОТИВОРЕЧИЕ
А – человек, юрист
В – человек, не юрист.
Слайд 10
ВЫСКАЗЫВАНИЯ
Высказывание – это повествовательное предложение, о котором можно
сказать, ложно оно или истинно.
Примеры:
Земля – планета Солнечной системы.
(Истина)
2+8<5
(Ложь)
Всякий квадрат есть параллелограмм.
(Истина)
Каждый параллелограмм есть квадрат.
(Ложь)
Уходя, гасите свет!
(Не высказывание.)
Да здравствуют каникулы!
(Не высказывание.)
Слайд 11
СЛОЖНОЕ ВЫСКАЗЫВАНИЕ
Сложное высказывание получается путем объединения простых высказываний
связками – союзами И, ИЛИ и частей НЕ.
Значение истинности
сложных высказываний зависит от истинности входящих в них простых высказываний и от объединяющих их связок.
Слайд 12
ЗАДАНИЕ
Даны 4 простых высказывания:
На улице идет дождь.
На улице
светит солнце.
На улице пасмурная погода.
На улице идет снег.
Составьте 2
сложных высказывания, одно из которых в любой ситуации будет ложно, а другое всегда истинно, обязательно используя все предложенные простые высказывания.
Слайд 13
Аристотель
Сочинения по логике, составившие свод «Органон» (труды «Категории»,
«Об истолковании», первая и вторая «Аналитика», «Топика»)
Слайд 14
Лейбниц
В духе рационализма развил учение о прирожденной способности
ума к познанию высших категорий бытия и всеобщих и
необходимых истин логики и математики («Новые опыты о человеческом разуме», 1704 г.). Предвосхитил принципы современной математической логики («Об искусстве комбинаторики», 1666 г.). Один из создателей дифференциального и интегрального исчислений.
Слайд 15
Джордж Буль
Буль (Boole) Джордж (2 ноября 1815 года,
Линкольн, Великобритания – 8 декабря 1864 года, Баллинтемпль, Ирландия),
английский математик и логик, один из основоположников математической логики. Разработал алгебру логики (булеву алгебру) («Исследование законов мышления»,1854 г.), основу функционирования цифровых компьютеров.
Слайд 16
ТОЖДЕСТВО
КРУГИ ЭЙЛЕРА
Отношение между объемами понятий можно проиллюстрировать с
помощью кругов Эйлера. Данная геометрическая иллюстрация предложена математиком, физиком
и астрономом Леонардом Эйлером (1707-1781)
Отношение между объемами понятий можно проиллюстрировать с помощью кругов Эйлера. Данная геометрическая иллюстрация предложена математиком, физиком и астрономом Леонардом Эйлером (1707-1781)
Слайд 17
ПЕРЕСЕЧЕНИЕ
КРУГИ ЭЙЛЕРА
Отношение между объемами понятий можно проиллюстрировать с
помощью кругов Эйлера. Данная геометрическая иллюстрация предложена математиком, физиком
и астрономом Леонардом Эйлером (1707-1781)
Слайд 18
ПОДЧИНЕНИЕ
КРУГИ ЭЙЛЕРА
Отношение между объемами понятий можно проиллюстрировать с
помощью кругов Эйлера. Данная геометрическая иллюстрация предложена математиком, физиком
и астрономом Леонардом Эйлером (1707-1781)
Слайд 19
СОПОДЧИНЕНИЕ
КРУГИ ЭЙЛЕРА
Отношение между объемами понятий можно проиллюстрировать с
помощью кругов Эйлера. Данная геометрическая иллюстрация предложена математиком, физиком
и астрономом Леонардом Эйлером (1707-1781)
Слайд 20
ПРОТИВОПОЛОЖНОСТЬ
КРУГИ ЭЙЛЕРА
Отношение между объемами понятий можно проиллюстрировать с
помощью кругов Эйлера. Данная геометрическая иллюстрация предложена математиком, физиком
и астрономом Леонардом Эйлером (1707-1781)