- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Первинний статистичний аналіз програмного забеспечення. (Лекція 10)
Содержание
- 2. Застосування статистики при аналізі результатів вимірювань ПЗ.Первинний статистичний аналіз.Закон розподілу.Статистичні перевірки.
- 3. Проблема аналізу вимірюваньНа основі вимірювання простих властивостей програмного забезпечення потрібно робити висновки про загальні його властивості
- 4. Застосування статистичного аналізу для ПЗІдентифікація розподілуПошук та відображення залежностей між данимипрогнозування
- 5. ВибіркаЦе деякий набір значень величини із загальної
- 6. ГістограмиПобудова варіаційного ряду (гістограми) вимагає ранжування результатів
- 7. ГістограмиДля побудови гістограми проводиться розбиття варіаційного ряду
- 8. ГістограмиКількість класів — величина довільна. Краще вибирати
- 9. Гістограми
- 10. Аналіз неперервних та дискретних данихНеперервні дані представляються
- 11. Математичне сподіванняСереднє арифметичне, яке є оцінкою математичного сподівання випадкової величини
- 12. Дисперсія та середнє квадратичне відхиленняВибіркова дисперсія та середньоквадратичне відхилення характеризує розсіювання вибіркових даних відносно середнього
- 13. Коефіцієнти асиметрії та ексцесуКоефіцієнт асиметрії, що характеризує
- 14. Довірчі інтервалиВикористовується для оцінювання точності оцінок параметрівtα/2,ν
- 15. Вилучення аномальних значеньОбчислені значення статистикиПорівнюється з критичним значенням ta/2,v (квантиль розподілу Стьюдента)При хгр підлягає видаленню
- 16. Вилучення аномальних значеньПідсумком аналізу варіаційного ряду або
- 17. Види розподілівОднопараметричніЕкспоненційнийРелеяМаксвелаПірсонаТ-розподіл СтьюдентаДвопараметричніРівномірнийПареттоНормальнийЛогарифмічно-нормальнийЛапласаГамма-розподілЕкстремальнийРозподіл Вейбула
- 18. Закон розподілуВикористовується для дискретної випадкової величиниПоказує множину можливих подій з ймовірностями їх настання
- 19. Ідентифікація розподілів (крок 1)На практиці при первинному
- 20. Ідентифікація розподілів
- 21. Ідентифікація розподілівУнімодальна гістограма:ЕкспоненційнийВейбула з параметром β 1Гамма-розподілЕкстремальнийЕрлангаМаксвеллаПірсона…
- 22. Ідентифікація розподілів (крок 2)Вибір конкретного типу розподілу
- 23. Ідентифікація розподілів – моментні характеристикиВибір розподілу базується
- 24. Відтворення розподілівМетою відтворення розподілів є побудова функції розподілу за вибірковими даними
- 25. Схема відтворення розподілівОсновні кроки1. Первинний статистичний аналіз2.
- 26. Схема відтворення розподілівПервинний статистичний аналізФормування варіаційних рядівРозбиття
- 27. Методи оцінки параметрів розподілуМетод максимальної правдоподібності –
- 28. Скачать презентацию
- 29. Похожие презентации
Застосування статистики при аналізі результатів вимірювань ПЗ.Первинний статистичний аналіз.Закон розподілу.Статистичні перевірки.

























Слайд 2
Застосування статистики при аналізі результатів вимірювань ПЗ.
Первинний статистичний
аналіз.
Слайд 3
Проблема аналізу вимірювань
На основі вимірювання простих властивостей програмного
забезпечення потрібно робити висновки про загальні його властивості
Слайд 4
Застосування статистичного аналізу для ПЗ
Ідентифікація розподілу
Пошук та відображення
залежностей між даними
прогнозування
Слайд 5
Вибірка
Це деякий набір значень величини із загальної кількості
її значень (генеральної сукупності).
Достатність вибірки – представлення вибіркою генеральної
сукупності (при збільшенні об’єму даних середні статистичні характеристики змінюються несуттєво)
Слайд 6
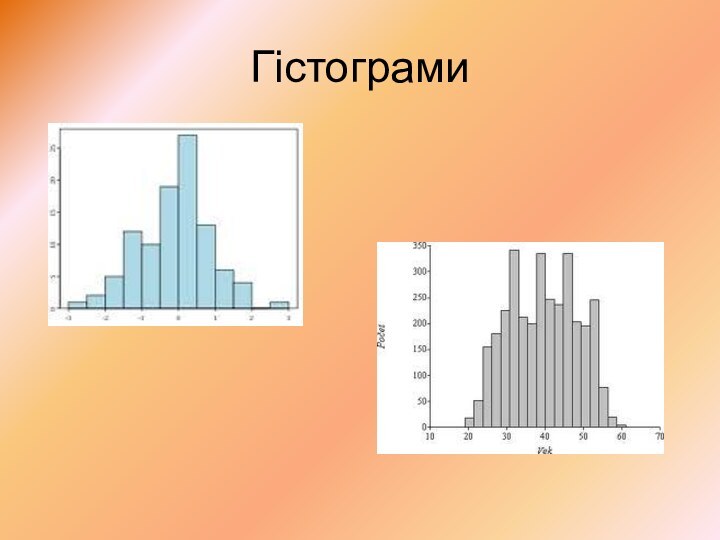
Гістограми
Побудова варіаційного ряду (гістограми) вимагає ранжування результатів спостережень
та обчислення відповідних їм частот і випадковостей:
х1,
х2, ..., хrn1, n2, ..., nr
f1, f2, ..., fr,
де r – кількість варіант;
хі – і-те значення х метрики;
ni – частота хі, ;
- випадковість хі.
Слайд 7
Гістограми
Для побудови гістограми проводиться розбиття варіаційного ряду на
класи. Для цього фіксується рівномірне розбиття осі спостережень ∆h
на класи, де h — крок розбиття. Крок розбиття визначається із співвідношення:а — початок спостережень (окремий випадок х1 = а);
b — кінець спостережень (окремий випадок хг = b );
т — кількість елементів розбиття ∆h (кількість класів).
Слайд 8
Гістограми
Кількість класів — величина довільна.
Краще вибирати т
непарним і таким, щоб гістограма, по можливості, не мала
осциляції випадковостей і була більш-менш "гладкою".Iснує оптимальна кількість класів, яка залежить від обсягу даних вибірки n та від типу їх закону розподілу (мається на увазі врахування асиметрії та ексцесу). При n < 100 можна використати формулу
Слайд 10
Аналіз неперервних та дискретних даних
Неперервні дані представляються у
вигляді функцій
При аналізі дискретні дані краще представляти у неперервній
формі
Слайд 11
Математичне сподівання
Середнє арифметичне, яке є оцінкою математичного сподівання
випадкової величини
Слайд 12
Дисперсія та середнє квадратичне відхилення
Вибіркова дисперсія та середньоквадратичне
відхилення характеризує розсіювання вибіркових даних відносно середнього
Слайд 13
Коефіцієнти асиметрії та ексцесу
Коефіцієнт асиметрії, що характеризує асиметричність
функції щільності (гістограми) відносно середнього
Коефіцієнт ексцесу характеризує гостровершинність
функції розподілу (гістограми) відносно нормального розподілу
Слайд 14
Довірчі інтервали
Використовується для оцінювання точності оцінок параметрів
tα/2,ν –
квантиль t-розподілу Стьюдента.
За величину беруть відповіді точкову оцінку,
а значення а визначають із співвідношень:
Слайд 15
Вилучення аномальних значень
Обчислені значення статистики
Порівнюється з критичним значенням
ta/2,v (квантиль розподілу Стьюдента)
При хгр підлягає видаленню
Слайд 16
Вилучення аномальних значень
Підсумком аналізу варіаційного ряду або гістограми
може бути попередній висновок про наявність аномальних ("грубих") значень
хгр .Візуально такі значення можна ідентифікувати з аналізу гістограм, коли значення варіаційного ряду досить суттєво віднесене від загальної сукупності даних та має порівняно малу випадковість.
Варіанта xі за своїм значенням може різко відхилятися від загальні сукупності варіант у двох випадках:
якщо вона належить до генеральної сукупності, як і основна група, проте є малоймовірною подією
або якщо має місце випадкове порушення умов експерименту.
Слайд 17
Види розподілів
Однопараметричні
Експоненційний
Релея
Максвела
Пірсона
Т-розподіл Стьюдента
Двопараметричні
Рівномірний
Паретто
Нормальний
Логарифмічно-нормальний
Лапласа
Гамма-розподіл
Екстремальний
Розподіл Вейбула
Слайд 18
Закон розподілу
Використовується для дискретної випадкової величини
Показує множину можливих
подій з ймовірностями їх настання
Слайд 19
Ідентифікація розподілів (крок 1)
На практиці при первинному статистичному
аналізі тип розподілу невідомий
Попередньо проводять ідентифікацію, аналізуючи гістограму (крок
1)
Слайд 21
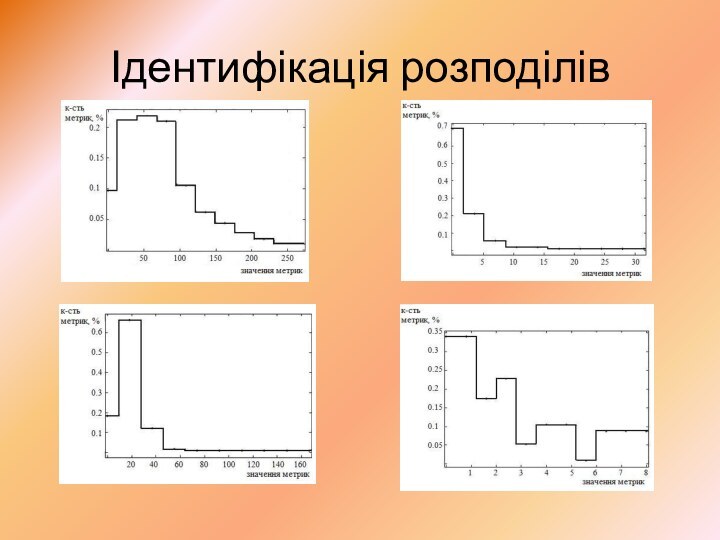
Ідентифікація розподілів
Унімодальна гістограма:
Експоненційний
Вейбула з параметром β
Стьюдента
Лапласа
Коші
Релея
Одномодальна асиметрична гістограма:
Логарифмічно-нормальний
Вейбула з параметром β > 1
Гамма-розподіл
Екстремальний
Ерланга
Максвелла
Пірсона
…
Слайд 22
Ідентифікація розподілів (крок 2)
Вибір конкретного типу розподілу за
емпіричною функцією розподілу (крок 2)
2 підходи:
Перетворення функції розподілу для
надання лінійного вигляду (переважно – перетворення Джонсона)Моментна ідентифікація – за допомогою коефіцієнтів асиметрії та ексцесу
Слайд 23
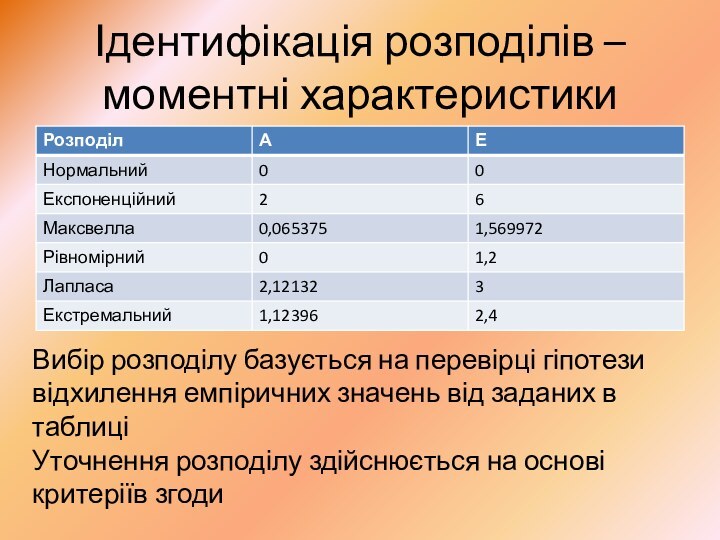
Ідентифікація розподілів – моментні характеристики
Вибір розподілу базується на
перевірці гіпотези відхилення емпіричних значень від заданих в таблиці
Уточнення
розподілу здійснюється на основі критеріїв згоди
Слайд 24
Відтворення розподілів
Метою відтворення розподілів є побудова функції розподілу
за вибірковими даними
Слайд 25
Схема відтворення розподілів
Основні кроки
1. Первинний статистичний аналіз
2. Знаходження
оцінок параметрів
3. Оцінювання точності оцінок параметрів шляхом обчислення дисперсії
та довірчих інтервалів4. Обчислення значень статистичної функції розподілу у точках варіаційного ряду
5. Визначення одного або кількох критеріїв згоди
6. Довірче оцінювання теоретичної функції розподілу ймовірностей
Слайд 26
Схема відтворення розподілів
Первинний статистичний аналіз
Формування варіаційних рядів
Розбиття варіаційних
рядів на класи
Вилучення аномальних значень
Обчислення емпіричної функції розподілу ймовірностей
Знаходження
статистичних характеристик вибірки з довірчим оцінюваннямІдентифікація типу розподілу
Слайд 27
Методи оцінки параметрів розподілу
Метод максимальної правдоподібності – відбувається
порівняння емпіричних та теоретичних статистичних характеристик
Метод моментів – базується
на порівнянні теоретичних та статистичних початкових або центральних моментівМетод найменших квадратів – використовується при ефективному перетворенні функції розподілу до лінійного вигляду