Презентация на тему Построение остовного (покрывающего) дерева графа

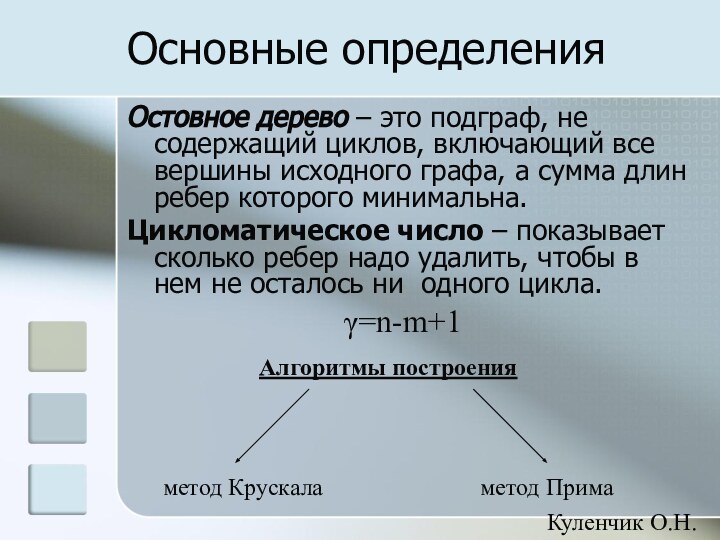
циклов, включающий все вершины исходного графа, а сумма длин

ребер которого минимальна.
Цикломатическое число – показывает сколько ребер надо удалить, чтобы в нем не осталось ни одного цикла.

Алгоритмы построения

метод Крускала

метод Прима

γ=n-m+1

Куленчик О.Н.

их весов, каждая вершина графа помещается в одноэлементное подмножество.

Просматривая ребра исходного графа, делается вывод о включении, либо исключении ребра из остовного дерева. При этом, если ребро связывает вершины, принадлежащие разным подмножествам, то оно включается в остовное дерево, в противном случае ребро удаляется из рассмотрения.

Куленчик О.Н.

остовное дерево методом Крускала.
Подсчитаем
цикломатическое
число
γ=n-m+1
Проверка сошлась, надо было

удалить 5 ребер и мы их удалили

γ=10-6+1=5

Куленчик О.Н.

для начального рассмотрения ее по отношению к другим вершинам.

После чего, выбирается минимальный вес (с вершиной). Вершину с минимальным весом удаляем из дальнейшего рассмотрения и сносим ее на следующий уровень. Дальше мы начинаем рассматривать снесенную вершину относительно других, оставшихся вершин.

Куленчик О.Н.

дерево методом Прима.
На первом шаге минимальный
вес был

1 и принадлежал он вершине V2, поэтому мы
ее выбираем и удаляем из дальнейшего рассмотрения.
На втором шаге мы рассматриваем вершину V2, т.к. ее
мы удалили, относительно оставшихся вершин. Причем
на втором шаге не только проставляем веса ребер, но и
сравниваем их с предыдущим уровнем. Если на
предыдущем уровне вес был меньше, то сносим min вес.

Заполним таблицу
весами ребер,
которые соединяют
рассматриваемые
вершины.

Куленчик О.Н.