- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Потоковые шифры. (Лекция 6)
Содержание
- 2. Действия противника:E1 + E2 = M1+γ+M2+γ= M1+M2;Т.о.
- 3. Подход к вскрытию книжного шифраM1=влесуродиласьелочкавлесуонаM2=россиясвященнаянашадержаварЕ =xxxxxxxxxxxxxxxxxxxxxxxxxxxДля вскрытия
- 4. Перебор словЕ =xxxxxxxxxxxxxxxxxxxxxxxxxxx1 елочка елочка
- 5. Потоковые шифрыПосимвольное шифрование.Каждый символ сообщения (независимо от
- 6. Потоковое шифрованиеГенератор Г(K)Г – шифрующая последовательностьГiMiEiГенератор Г(K)ГiEiMiК – по секретному каналуE – по открытому каналу
- 7. Потоковые шифрыБольшинство потоковых шифров – аддитивные (шифрование
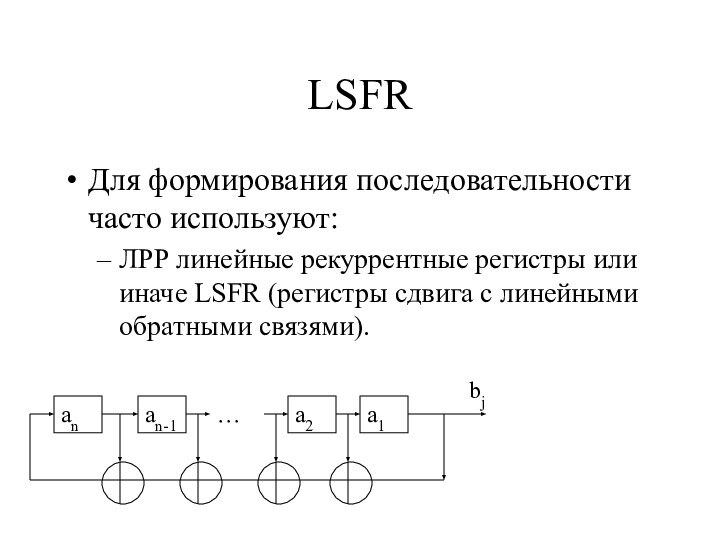
- 8. LSFRДля формирования последовательности часто используют:ЛРР линейные рекуррентные
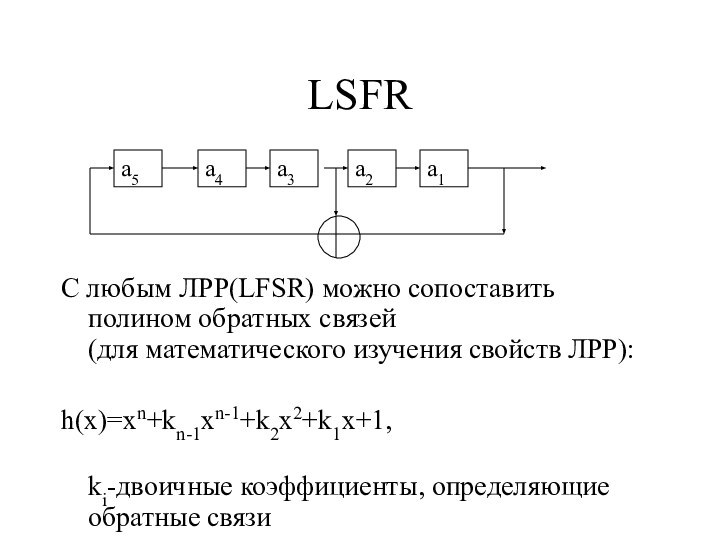
- 9. LSFRa5a4a3a2a1С любым ЛРР(LFSR) можно сопоставить полином обратных
- 10. Свойства LSFR:Период выходной последовательности T
- 11. Выходная последовательность ЛРР, основанного на примитивном полиноме
- 12. Свойство окна110101111001011010001110101111001011010001110101111001011010001110Обратная связь
- 13. Недостаток генератора Г на основе ЛРРНепосредственно использовать
- 14. Полиномиальная сложность восстановления регистра по выходной последовательности
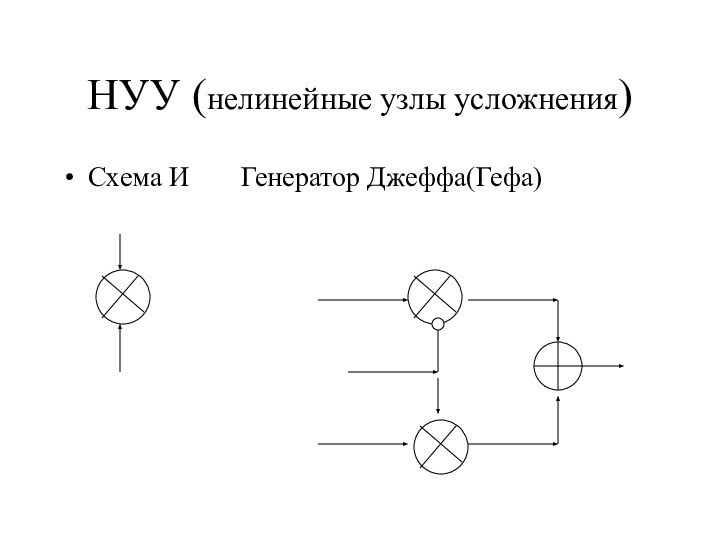
- 15. НУУ (нелинейные узлы усложнения)Схема И Генератор Джеффа(Гефа)
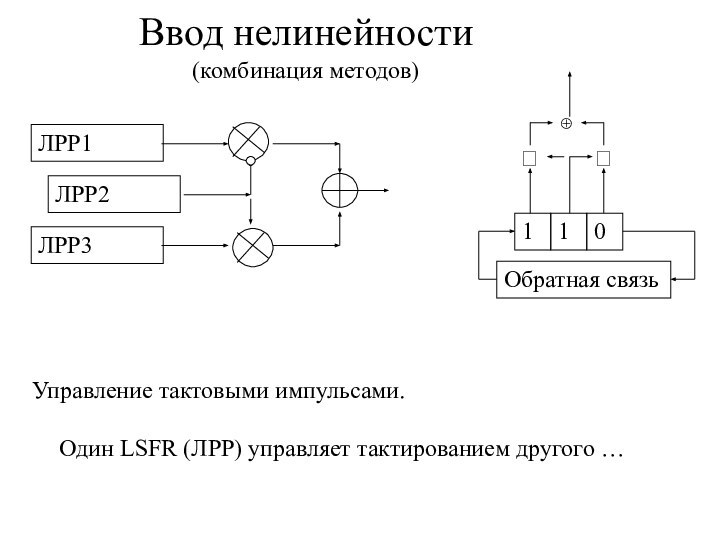
- 16. Ввод нелинейности (комбинация методов)ЛРР1ЛРР2Управление тактовыми импульсами. Один LSFR (ЛРР) управляет тактированием другого …ЛРР3110Обратная связь⊕⮾⮾
- 17. Эквивалентный регистрЛюбой совокупности ЛРР и НУУ можно сопоставить один эквивалентный ЛРР большей длины. dэкв >> Σ dЛРР(i)i
- 18. Свойства потоковых шифров*Простота схем и низкая стоимостьВысокая
- 19. Примеры потоковых шифровA5 (шифрование в GSM)ЛРР(22)ЛРР (19)ЛРР(23)Схема упр. тактированием81010
- 20. Особенности A5 (недостатки)Первоначально секретный алгоритмA5/1 ~ 240 *A5/2 менее стойкий
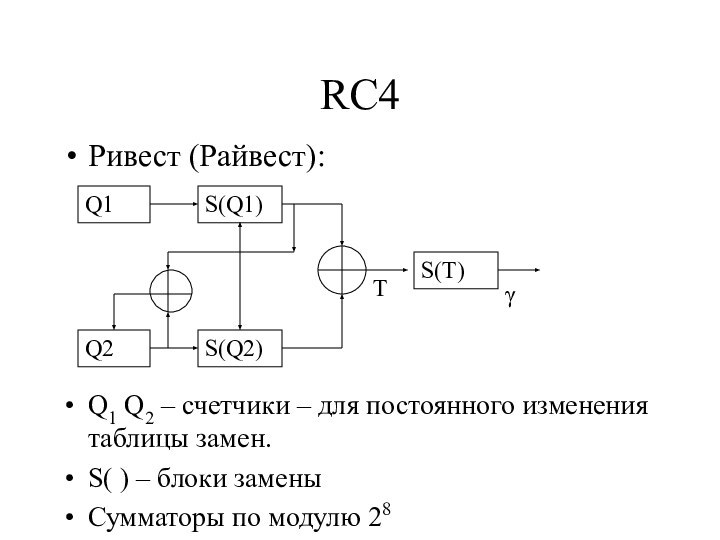
- 21. RC4Ривест (Райвест):Q1Q2S(Q1)S(Q2)S(T)TγQ1 Q2 – счетчики – для
- 22. RC4Q1=(Q1+1)mod 28Q2=(Q2+S[Q1])mod 28S[Q1] S[Q2] - обмен значениямиТ=
- 23. Скачать презентацию
- 24. Похожие презентации
Действия противника:E1 + E2 = M1+γ+M2+γ= M1+M2;Т.о. Противник свел потоковый шифр к книжному (один осмысленный текст шифруется другим осмысленным текстом).
![RC4Q1=(Q1+1)mod 28Q2=(Q2+S[Q1])mod 28S[Q1] S[Q2] - обмен значениямиТ= (S[Q1]+S[Q2])mod 28γ = S[T];Для работы](/img/tmb/15/1428843/87c54dc50bb63539bec989454d207c57-720x.jpg "Потоковые шифры. (Лекция 6)")
Слайд 3
Подход к вскрытию книжного шифра
M1=влесуродиласьелочкавлесуона
M2=россиясвященнаянашадержавар
Е =xxxxxxxxxxxxxxxxxxxxxxxxxxx
Для вскрытия может
использоваться частотный словарь словоформ русского языка (для другого типа
данных аналогичный словарь надо составлять самостоятельно).
Слайд 4
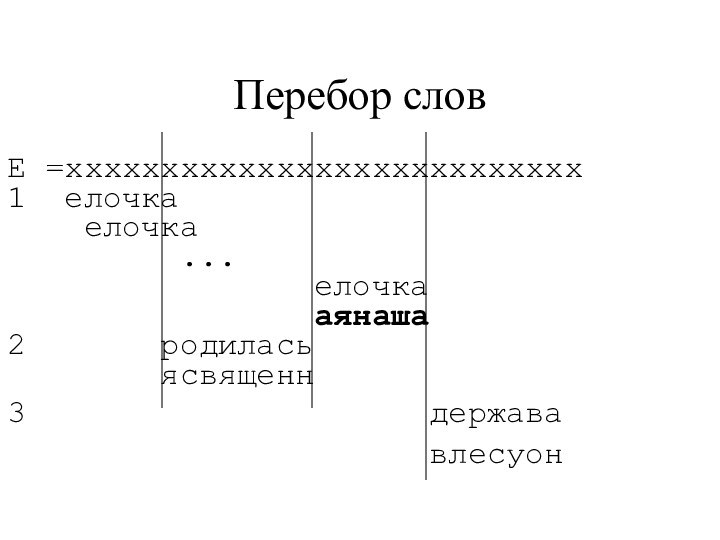
Перебор слов
Е =xxxxxxxxxxxxxxxxxxxxxxxxxxx
1 елочка
елочка
...
елочкааянаша
2 родилась
ясвященн
3 держава
влесуон
Слайд 5
Потоковые шифры
Посимвольное шифрование.
Каждый символ сообщения (независимо от других)
преобразуется в символ криптограммы по правилу, определяемому ключом. Ключ
меняется от символа к символу.Исторически первое применение –Вернам для телеграфных линий.
Слайд 6
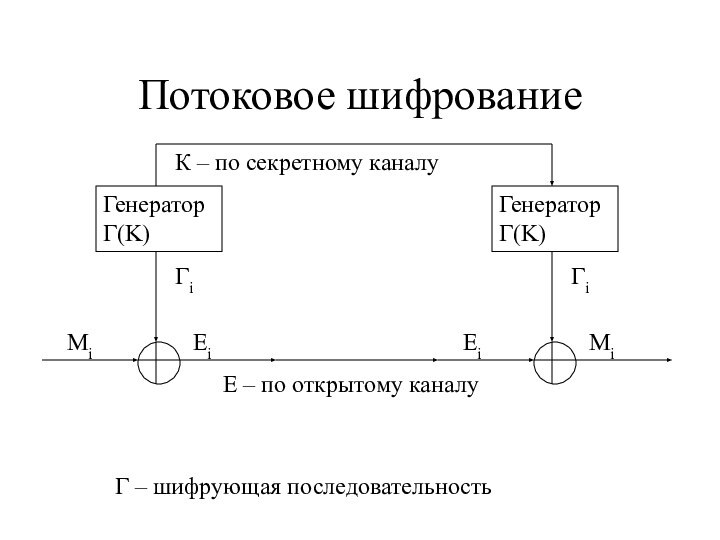
Потоковое шифрование
Генератор Г(K)
Г – шифрующая последовательность
Гi
Mi
Ei
Генератор Г(K)
Гi
Ei
Mi
К –
по секретному каналу
E – по открытому каналу
Слайд 7
Потоковые шифры
Большинство потоковых шифров – аддитивные (шифрование по
модулю 2)
Отличаются друг от друга принципом формирования шифрующей последовательности
Слайд 8
LSFR
Для формирования последовательности часто используют:
ЛРР линейные рекуррентные регистры
или иначе LSFR (регистры сдвига с линейными обратными связями).
an
an-1
…
a2
a1
bj
Слайд 9
LSFR
a5
a4
a3
a2
a1
С любым ЛРР(LFSR) можно сопоставить полином обратных связей
(для математического изучения свойств ЛРР):
h(x)=xn+kn-1xn-1+k2x2+k1x+1,
ki-двоичные коэффициенты, определяющие обратные связи
Слайд 10
Свойства LSFR:
Период выходной последовательности T
если ЛРР основан на примитивном полиноме:
Примитивный полином
неприводимый – не
представим в виде произведения полиномов меньшей степени.делит Xk+1, где k = 2n-1, но не делит Xd+1 для любого d, такого, что d делит 2n-1
Примитивные полиномы существуют для всех степеней. Существуют методы, позволяющие проверить на примитивность произвольный полином.
Слайд 11
Выходная последовательность ЛРР, основанного на примитивном полиноме обладает
свойствами:
баланса – равенство количество нулей и единиц (единиц на
одну больше)окна – выходная последовательность содержит все возможные варианты заполнения регистров (кроме нулевого) по одному разу.
Слайд 12
Свойство окна
110
101
111
001
011
010
001
110101111001011010001110101111001011010001
1
1
0
Обратная связь
Слайд 13
Недостаток генератора Г на основе ЛРР
Непосредственно использовать ЛРР
для шифрования нельзя, так как существует алгоритм (Месси-Берликампа), который
по 2n символам выходной последовательности восстанавливает вид обратных связей и начальное заполнение. Сложность алгоритма ~n3 n – длина регистра сдвига.
Слайд 14
Полиномиальная сложность восстановления регистра по выходной последовательности обусловлена
его линейностью.
Для устранения данного недостатка в схему формирования Г
вводят нелинейные элементы
Слайд 16
Ввод нелинейности
(комбинация методов)
ЛРР1
ЛРР2
Управление тактовыми импульсами.
Один LSFR (ЛРР) управляет
тактированием другого …
ЛРР3
1
1
0
Обратная связь
⊕
⮾
⮾
Слайд 17
Эквивалентный регистр
Любой совокупности ЛРР и НУУ можно сопоставить
один эквивалентный ЛРР большей длины.
dэкв >> Σ dЛРР(i)
i
Слайд 18
Свойства потоковых шифров*
Простота схем и низкая стоимость
Высокая скорость
Нет
размножения ошибок
Нет задержек
Проще оценивается стойкость.
* - по сравнению с
блоковыми
Слайд 19
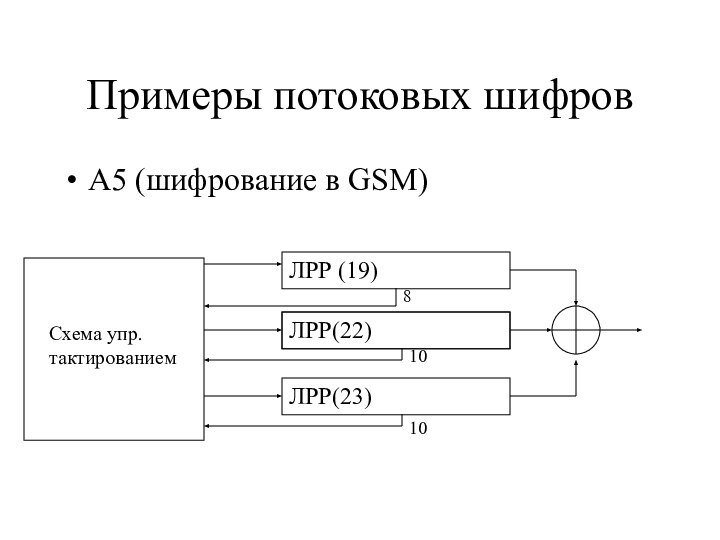
Примеры потоковых шифров
A5 (шифрование в GSM)
ЛРР(22)
ЛРР (19)
ЛРР(23)
Схема упр.
тактированием
8
10
10
Слайд 20
Особенности A5 (недостатки)
Первоначально секретный алгоритм
A5/1 ~ 240 *
A5/2 менее стойкий ~218 *
*
- при атаке по известной гамме.
Полиномы обратных связей разрежены
(для упрощения аппаратной реализации, но при этом несколько снижается стойкость.)Шифруются данные только между абонентом и базовой станцией.
Слайд 21
RC4
Ривест (Райвест):
Q1
Q2
S(Q1)
S(Q2)
S(T)
T
γ
Q1 Q2 – счетчики – для постоянного
изменения таблицы замен.
S( ) – блоки замены
Сумматоры по модулю
28
Слайд 22
RC4
Q1=(Q1+1)mod 28
Q2=(Q2+S[Q1])mod 28
S[Q1] S[Q2] - обмен значениями
Т=
