Слайд 2
НЕМНОГО ИСТОРИИ
Теория игр -раздел математики, в котором изучаются
математические модели принятия оптимальных решений в условиях конфликта, т.
е. при явлении, в котором участвуют различные стороны, наделенные различными возможностями выбирать доступные для них действия в соответствии с их интересами.
Схемы теории игр охватывают как собственно игры (шахматы, домино), так и различные ситуации, возникающие в экономических, военных и других вопросах.
Слайд 3
Математическая теория игр берёт своё начало
из неоклассической экономики. Впервые математические аспекты и приложения теории
были изложены в классической книге 1944 года Джона фон Неймана и Оскара Моргенштерна «Теория игр и экономическое поведение.
НЕМНОГО ИСТОРИИ
Эта область математики нашла некоторое отражение в общественной культуре. В 1998 году американская писательница и журналистка Сильвия Назар издала книгу о судьбе Джона Нэша, нобелевского лауреата по экономике и учёного в области теории игр; а в 2001 по мотивам книги был снят фильм «Игры разума».
Слайд 4
Подходы к принятию решений с позиций теории игр
Существует
бесконечно большое число вариантов игр. В случае, когда игроки
имеют только две возможных альтернативы и результаты могут быть выражены комбинацией четырех результатов 1, 2, 3 и 4, общее число различных матриц составляет 78 штук, из которых 12 симметричных. В случае трех альтернатив можно составить почти два миллиарда различных игр.
Имеется целый ряд игр, которые были подвергнуты детальному анализу. По некоторым из них проведены многочисленные эксперименты и написаны тысячи статей.
Теория игр позволяет лучше понять связи между действиями и соответствующими изменениями внешней среды и тем самым улучшить стратегии принятия решений.
Слайд 5
Подходы к принятию решений с позиций теории игр
Теория
игр нашла применение в самых различных областях человеческой деятельности.
Теория
показала, что везде, где возникает соревнование за ограниченные ресурсы, длительное и стабильное равновесие может установиться только в том случае, если игроки применяют смешанные стратегии, т.е. когда в игре применяется многообразие отдельных линий поведения, стилей мышления и стратегий решения проблем.
Слайд 6
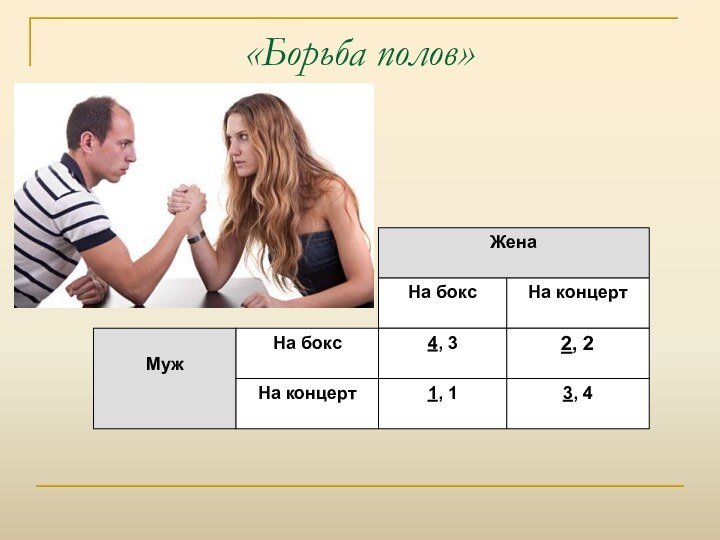
Наиболее известные модели теории игр
Долларовый аукцион
Дилемма заключенного
Лотерея Хофстеда
Борьба
полов
Вожак
Цыпленок
Слайд 7
Надо помнить, что теория игр ориентируется только на
рациональность целей. Рациональность ценностей ею не учитывается.
Использование стратегии теории
игр позволяет во многих случаях оптимизировать решение. В 1994 г. за успехи в развитии теории игр трем ученым J.F. Nash, J.C. Harsanyi и R. Selten была присуждена Нобелевская премия по экономике.
Наиболее известные модели теории игр
Слайд 8
Игры с осмысленной реакцией противника
Различают случаи с разным
числом участников: два, несколько, много и почти бесконечное число.
Концепции для случая большого числа участников значительно сложнее, поскольку приходится считаться с их разной реакцией, возможностью формирования коалиций и др.
Слайд 9
Отличают игры с однозначно определенными правилами, для которых
имеется полная информация об игровых ситуациях и правилах, и
игры с неоднозначными правилами.
В первых существует стратегия, которая каждому участнику обеспечивает принципиальную возможность успеха, независимо от поведения второго участника.
Для игр с неоднозначными правилами таких стратегий не существует. Поэтому такие игры характеризуются определенной нестабильностью, и каждый участник пытается заранее распознать поведение другого.
Игры с осмысленной реакцией противника
Слайд 10
Выбор стратегии может зависеть еще и от того,
выполняют ли игроки свои ходы одновременно или последовательно, а
также от того, делает ли участник первый ход или ответный ход. Решение будет зависеть и от того, имеет ли участник только один ход или ряд ходов.
Для выбора стратегии имеет также значение, является ли игра «игрой с постоянной суммой», называемой также «игрой с нулевой суммой», или общей игрой двух лиц.
В случае игры с «нулевой суммой» для каждой пары альтернатив сумма выплат остается постоянной – сумма проигрыша равна сумме выигрыша. Здесь также важно имеет ли игра точку равновесия (седловину). Если такая седловина существует, то при отклонении от нее каждый игрок рискует ухудшить свое положение.
Игры с осмысленной реакцией противника
Слайд 11
В общей игре двух лиц существует, по крайней
мере, одна пара альтернатив (комбинация действий двух игроков) при
которой сумма пользы игроков больше или меньше, чем при других парах альтернатив.
В общей игре двух лиц, называемой также игрой со смешенной мотивацией, игроки могут не только выиграть или проиграть то, что проигрывает или выигрывает противник, но иногда все игроки могут эффективно использовать ресурсы или избежать убытков, когда они сотрудничают. В этих играх индивидуальные и общие интересы смешаны.
Типичным примером игры со смешанной мотивацией является защита окружающей среды. С одной стороны в индивидуальных интересах каждого загрязнителя среды платить за это как можно меньше, с другой стороны все вместе они заинтересованы в защите окружающей среды.
Игры с осмысленной реакцией противника
Слайд 12
Общая игра двух игроков часто иллюстрируется, так называемой,
«дилеммой заключенного». «Дилемма заключенного» демонстрирует, что индивидуальная рациональность ведет
к коллективной нерациональности и как следствие к вреду для себя самого.
В общественной жизни и в бизнесе случаев, которые сводятся к дилемме заключенного сколько угодно, поэтому возникает вопрос о том, как с ними обходиться. Призывы вести себя кооперативно, хотя они и нужны, помогают мало. Нужны реальные санкции, контрольные механизмы, но также и рыночные льготы.
Игры с осмысленной реакцией противника
Слайд 13
Общие рекомендации по применению правил принятия решений в
ситуациях игры двух лиц:
Если партнер по игре делает ход
первым или при одновременном действии обоих намерение первого второму не известно, то представляется целесообразным исходить из правила Байеса, т.е. из того, что в единичном случае наибольшая надежность успеха соответствует наиболее вероятной стратегии.
Если риск опасен или, по крайней мере, показана осторожность, то следует предпочесть правило минимакса (правило Вальда). ЛПР выбирает ту альтернативу, которая при наиболее неблагоприятной для него ситуации дает относительно лучший результат. Такие случаи имеют место, когда ЛПР должен делать первый ход, или в ситуации, когда оба делают ходы одновременно, но имеется точка равновесия (седловина).
Игры с осмысленной реакцией противника
Слайд 14
Матрица решений для «дилеммы заключенного»
Подчеркнутая цифра показывает результат
для первого заключенного, вторая цифра – для второго заключенного.
Слайд 15
Cпираль гонки вооружений
Очевидно, что для каждой стороны превосходство
лучше дешевого равновесия, а дорогое равновесие лучше незащищенности.
Равновесие
двух противников может быть обеспечено как в случае, когда обе стороны вооружены до зубов, так и на существенно более низком уровне, что гораздо дешевле. Поэтому такой вариант является для обеих сторон самым выгодным.
Однако каждая сторона стремится ни в коем случае не допустить превосходства другой стороны, поэтому тратит все больше средств на вооружение.
Оптимальным для обеих сторон вариантом было бы дешевое равновесие, но этому мешает отсутствие доверия.
Слайд 17
«Дилемма заключенного» для случая игры со многими ходами
Слайд 18
«Дилемма заключенного» для случая игры со многими ходами
Победа
присуждалась программе, получившей максимальное суммарное число очков. В турнире
участвовало 15 программ. Победила программа известного специалиста по социальной психологии Анатолия Рапопорта.
Ее алгоритм был очень прост:
Сотрудничай в первом круге.
Делай то, что сделал твой противник в первом круге.
Рапопорт назвал свою программу «Tit for Tat» («Зуб за зуб»). В литературе по теории игр ее обозначают TFT.
Слайд 19
Для лучших программ были характерны два признака: дружелюбие
и снисходительность.
Аксельрод называл программу дружелюбной, если она никогда
не начинала конкурировать первой.
Снисходительной он называл программу, если она после противостояния была готова возвратиться к кооперированию, как только противник начинал кооперировать.
Важнейшим результатом исследований Аксельрода является то, что теоретически установление стабильного кооперирования даже в тотально эгоистическом окружении не исключается. Все программы были ориентированы на выигрыш и руководствовались исключительно эгоистическими соображениями, а не альтруизмом или сложными моральными принципами. Если у живого существа разовьется ген TFT, оно способно к кооперации даже в условиях, когда его цели полностью эгоистичны.
Слайд 20
Если ты нажмешь эту кнопку, ты кооперируешь со
своим партнером и даешь ему две единицы, а себе
одну единицу. Если ты нажимаешь вторую кнопку, ты даешь себе две единицы, а партнеру ни одной. Твой партнер имеет те же возможности
Слайд 21
Эксперименты показали, что при некотором изменении матрицы кооперация
между игроками развивается гораздо чаще. Это связано, вероятно, с
тем, что здесь наглядно видно: мы можем выиграть много только в том случае, если партнер нам помогает, т.е. кооперирует. В реальной жизни таким регулятором может стать стимулирующее законодательство, общественное мнение, профессиональные кодексы.
Слайд 25
Рациональность нерационального мышления
Нейробиологам удалось уже давно локализовать многие
группы клеток в мозгу человека, которые отвечают за определенные
задачи.
Однако до сих пор не удавалось удовлетворительно локализовать какую-то область мозга, которая определяет сознательное и рациональное мышление.
Учеными выдвинута гипотеза о том, что мозг организован не по иерархическому принципу, а по голографическому. При этом каждая часть мозга владеет всей информацией. Имеется и определенное экспериментальное подтверждение этой гипотезы.
Слайд 26
Рациональность нерационального мышления
Связи между нашими решениями и результирующими
плохими или хорошими событиями вызывают особые вторичные чувственные реакции,
которые Антонио Дамасио назвал соматическими маркерами. Эти маркеры определяют наши решения тем, что они за счет плохого или хорошего ощущения «под ложечкой» или в какой-либо другой части тела подсказывают нам, что рассматриваемая нами возможность многообещающа или опасна.
Слайд 27
Рациональность нерационального мышления
Под эволюционно стабильной стратегией понимается такая,
к которой должна бы прийти популяция живых существ, чтобы
обеспечить биологическое выживание.
Группа из многих людей, которые независимо друг от друга принимают нерациональные решения, в состоянии вести себя коллективно рационально, т.е. в соответствии с оптимальной смешанной стратегией.
Можем ли мы быть абсолютно уверены в том, что сознательное мышление рационально, а другие неосознанные силы иррациональны?
Использование соматических маркеров в процессе мышления не является ни чисто рациональным, ни иррациональным.