- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение задач оптимизации в MS Excel
Содержание
- 2. Для решения задач оптимизации необходимо:Задать целевую функцию Создать математическую модель задачиРешить задачу на компьютере
- 3. Математическая модельМатематическая модель – это приближенное описание
- 4. ЗадачаКомпания производит полки для ванных комнат двух
- 5. Целевая функцияОчевидно, что в качестве критерия оптимизации
- 6. Ограничение на объем производства:«…Агенты по продаже считают,
- 7. Ограничение на использование оборудования:«…Для изготовления одной полки
- 8. Ограничение на использование материалов:«…Для каждой полки типа
- 9. Граничные условияВ качестве граничных условий в данном
- 10. Ввод условий задачи Ввод условий задачи состоит из
- 11. Создание формы для ввода данных Такая форма должна
- 12. Ввод исходных данныхОтметим, что целевая функция и
- 13. Назначение целевой функции, ввод ограничений и граничных
- 14. Назначить целевую ячейкуДля этого в поле «Установить
- 15. Ввести ограничения и граничные условияВвести ограничения и
- 16. Получение результатаПосле нажатия на кнопку Выполнить диалогового
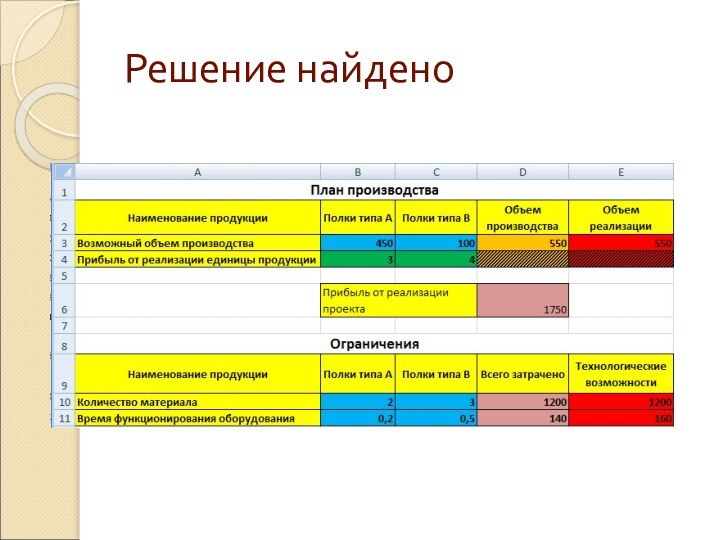
- 17. Решение найдено
- 18. Скачать презентацию
- 19. Похожие презентации
Для решения задач оптимизации необходимо:Задать целевую функцию Создать математическую модель задачиРешить задачу на компьютере















Слайд 2
Для решения задач оптимизации необходимо:
Задать целевую функцию
Создать
математическую модель задачи
Слайд 3
Математическая модель
Математическая модель – это приближенное описание какого-либо
класса явлений средствами математической символики.
При составлении математической модели
решения задачи оптимизации искомые величины принимаются за неизвестные и составляется система неравенств, наиболее полно характеризующих решение поставленной задачи. В любую математическую модель входят две составляющие:
Ограничения, которые устанавливают зависимости между переменными.
Граничные условия показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении.
Слайд 4
Задача
Компания производит полки для ванных комнат двух типов
- А и В. Агенты по продаже считают, что
за неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, для полки типа В - 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин. работы оборудования, а для изготовления одной полки типа В - 30 мин. Оборудование можно использовать 160 час. в неделю. Если прибыль от продажи полок типа А составляет 3 долл., а от полок типа В - 4 долл., то сколько полок надо выпускать в неделю, чтобы получить максимальную прибыль?
Слайд 5
Целевая функция
Очевидно, что в качестве критерия оптимизации в
данном случае выступает функция прибыли. Оптимальным будет считаться тот
из вариантов решения, в котором значение прибыли будет максимальным. Учитывая, что «…прибыль от продажи полок типа А составляет 3 долл., а от полок типа В - 4 долл.…» целевая функция будет выглядеть следующим образом:3x1 + 4x2 ⇒ max, где
x1 – объем производства полок типа A
x2 – объем производства полок типа B
Слайд 6
Ограничение на объем производства:
«…Агенты по продаже считают, что
неделю на рынке может быть реализовано до 550 полок…»
Очевидно, что совокупный объем производства полок не должен превышать 550 единиц, или, в математическом виде:x1 + x2 ≤ 550
Слайд 7
Ограничение на использование оборудования:
«…Для изготовления одной полки типа
А требуется 12 мин. работы оборудования, а для изготовления
одной полки типа В - 30 мин. Оборудование можно использовать 160 часов в неделю…» На основе этой информации можно сделать вывод, что общее время использования оборудования в рамках данного проекта не должно превышать 160 часов в неделю. Переведя время, необходимое для изготовления одной полки в часы (с целью сопоставимости единиц измерения правой и левой части неравенства) получим:0,2x1 + 0,5x2 ≤ 160
Слайд 8
Ограничение на использование материалов:
«…Для каждой полки типа А
требуется 2 м2 материала, для полки типа В -
3 м2 материала. Компания может получить до 1200 м2 материала в неделю…» На основе этой информации можно сделать вывод, что общее количество материала, затрачиваемого для реализации данного проекта, не должно превышать 1200 м2:2x1 + 3x2 ≤ 1200
Слайд 9
Граничные условия
В качестве граничных условий в данном примере
могут быть использованы следующие утверждения, вытекающие из сути поставленной
задачи:Объем производства полок типа А и полок типа В – неотрицательное значение.
Объем производства полок типа А и полок типа В – целое число, запишем таким образом:
x1, x2 ≥ 0
x1, x2 – целое
Слайд 10
Ввод условий задачи
Ввод условий задачи состоит из следующих
основных шагов:
Создание формы для ввода данных, необходимых для последующего
решения.Ввод исходных данных и зависимостей из математической модели.
Указание целевой ячейки (ячейки, в которую введена целевая функция), ввод ограничений и граничных условий в диалоговом окне Поиск решения.
Слайд 11
Создание формы для ввода данных
Такая форма должна содержать
возможность ввода всех данных, необходимых для решения поставленной задачи:
искомых
переменных;целевой функции;
правой и левой части неравенств, описывающих ограничения, налагаемые на возможные варианты решения поставленной задачи.
Слайд 12
Ввод исходных данных
Отметим, что целевая функция и левые
части неравенств, определяющих возможные варианты решения поставленной задачи, вводятся
формулой, в которой роль искомых переменных играют адреса ячеек, зарезервированных для вывода их значений после решения задачи, а роль коэффициентов – адреса ячеек, содержащих соответственные коэффициенты.
Слайд 13
Назначение целевой функции, ввод ограничений и граничных условий
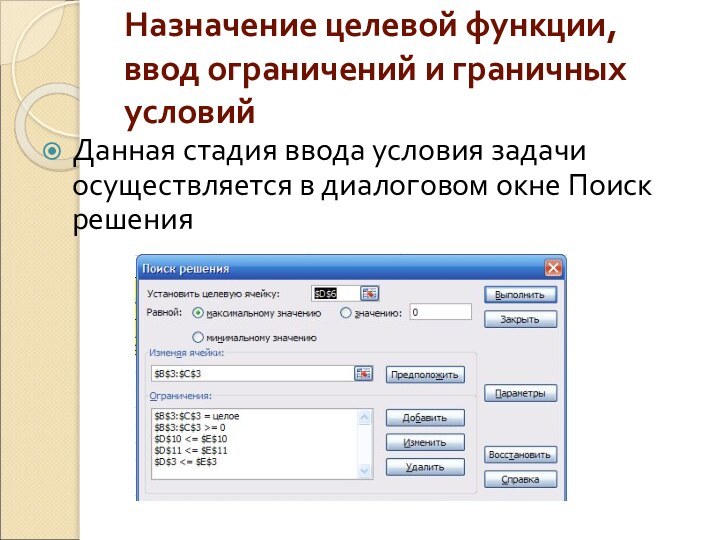
Данная
стадия ввода условия задачи осуществляется в диалоговом окне Поиск
решения
Слайд 14
Назначить целевую ячейку
Для этого в поле «Установить целевую
ячейку:» вводится адрес ячейки, содержащей целевую функцию. Затем устанавливается
направление последней – значение, к которому она должна стремиться исходя из условий задачи (минимальное, максимальное, конкретное, задаваемое пользователем).В поле «Изменяя ячейки:» ввести адреса ячеек, зарезервированных для искомых переменных.
Слайд 15
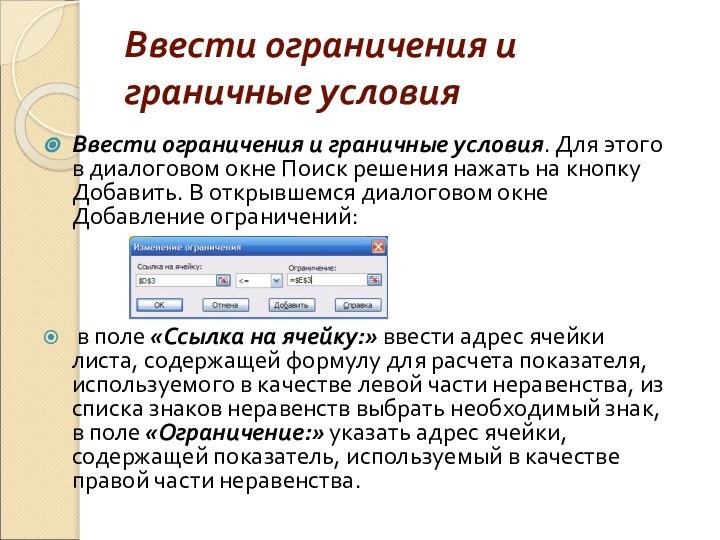
Ввести ограничения и граничные условия
Ввести ограничения и граничные
условия. Для этого в диалоговом окне Поиск решения нажать
на кнопку Добавить. В открывшемся диалоговом окне Добавление ограничений:в поле «Ссылка на ячейку:» ввести адрес ячейки листа, содержащей формулу для расчета показателя, используемого в качестве левой части неравенства, из списка знаков неравенств выбрать необходимый знак, в поле «Ограничение:» указать адрес ячейки, содержащей показатель, используемый в качестве правой части неравенства.