Слайд 2
ROPE
Rope — структура данных для хранения строки, представляющая
из себя двоичное сбалансированное дерево и позволяющая делать операции
вставки, удаления и конкатенации с логарифмической асимптотикой.
Иногда, при использовании строк нам нужны следующие свойства:
Операции которые часто используются на строках, должны быть более эффективными. Например: конкатенация, взятие подстроки.
Также эти операции должны эффективно работать и с длинными строками. Не должно быть прямой зависимости от длинны строк.
Персистентность. Иногда необходимо при изменении строки сохранить ее состояние перед изменением и вернуться к нему, если необходимо.
В данном случае Rope удовлетворяет всем этим свойствам.
Слайд 3
ROPE
В таблице приведены трудоемкости операций очереди с приоритетом:
Слайд 4
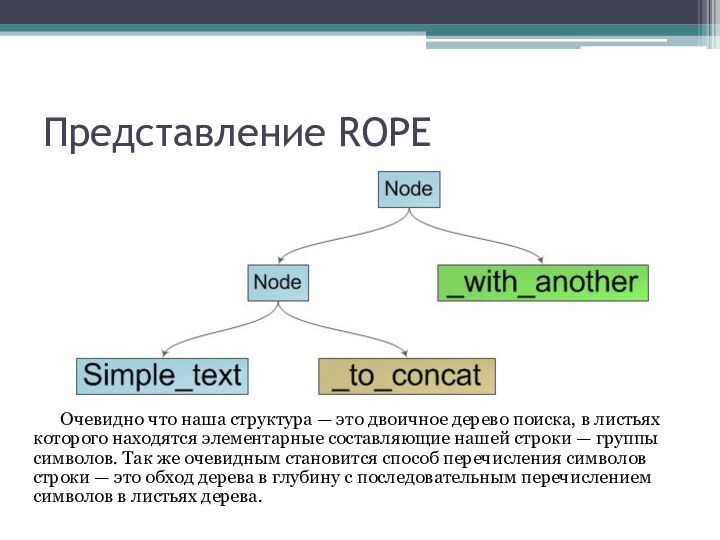
Представление ROPE
Очевидно что наша структура — это двоичное
дерево поиска, в листьях которого находятся элементарные составляющие нашей
строки — группы символов. Так же очевидным становится способ перечисления символов строки — это обход дерева в глубину с последовательным перечислением символов в листьях дерева.
Слайд 5
Представление ROPE
Узлы дерева имеют характеристику — вес. Если
в узле дерева хранится непосредственно часть символов (узел —
лист) то его вес равен количеству этих символов. Иначе, вес узла равен сумме весов его потомков. Иными словами, вес узла — длина строки, которую он представляет.
Слайд 6
Представление ROPE
Структура будет имет следующий вид:
struct trie
{
char *string;
int
length;
struct trie *left;
struct trie *right;
};
Слайд 7
Создание узла ROPE
struct trie *trie_create(char *string)
{
struct trie *node;
if ((node = (trie*)malloc(sizeof(*node))) == NULL)
return NULL;
node->string =
string;
node->length = strlen(node->string);
node->left = NULL;
node->right = NULL;
return node;
}
Слайд 8
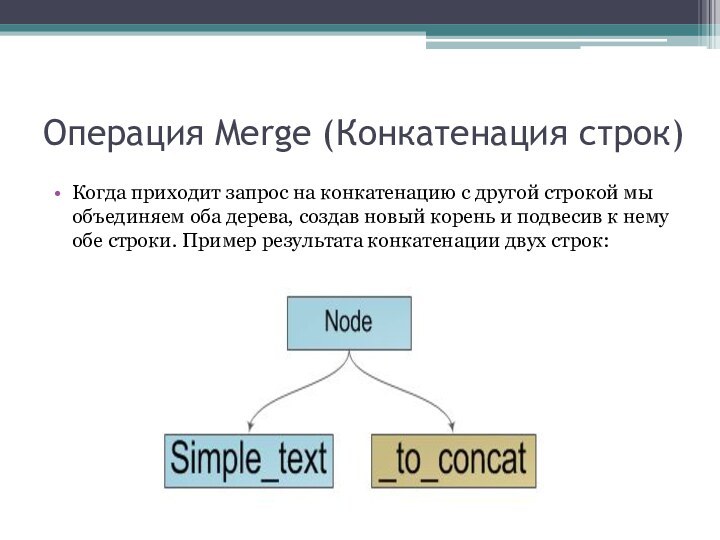
Операция Merge (Конкатенация строк)
Когда приходит запрос на конкатенацию
с другой строкой мы объединяем оба дерева, создав новый
корень и подвесив к нему обе строки. Пример результата конкатенации двух строк:
Слайд 9
Операция Merge (Конкатенация строк)
struct trie *merge(struct trie *trie1,
struct trie *trie2)
{
struct trie *node;
if ((node = (trie*)malloc(sizeof(*node))) ==
NULL)
return NULL;
if (trie1 == NULL || trie2 == NULL)
return NULL;
node->left = trie1;
node->right = trie2;
node->string = "";
node->length = node->left->length + node->right->length;
return node;
}
Слайд 10
Получение символа по индексу
Чтобы получить символ по некоторому
индексу , будем спускаться по дереву из корня, используя веса
записанные вершинах чтобы определить в какое поддерево пойти из текущей вершины. Алгоритм выглядит следующим образом:
Текущая вершина — не лист, тогда возможно два варианта:
Вес левого поддерева больше либо равен , тогда идем в левое поддерево.
Иначе идем в правое поддерево и ищем там символ, где вес левого поддерева.
Текущая вершина — лист, тогда в этом листе хранится ответ, необходимо взять символ с соответствующим номером у строки которая там хранится.
Слайд 11
Получение символа по индексу
char get(int i, struct trie
*node)
{
if (node->left != NULL)
if (node->left->length >= i)
return get(i, node->left);
else
return
get(i - node->left->length, node->right);
else
return node->string[i];
}
Слайд 12
Split (Разбиение строки)
Чтобы разбить строку на две по
некоторому индексу необходимо спускаясь по дереву (аналогично операции ), каждую вершину
на пути поделить на две, каждая из которых будет соответствовать одно из половинок строк, при этом необходимо после деления пересчитать вес этих вершин.
Слайд 13
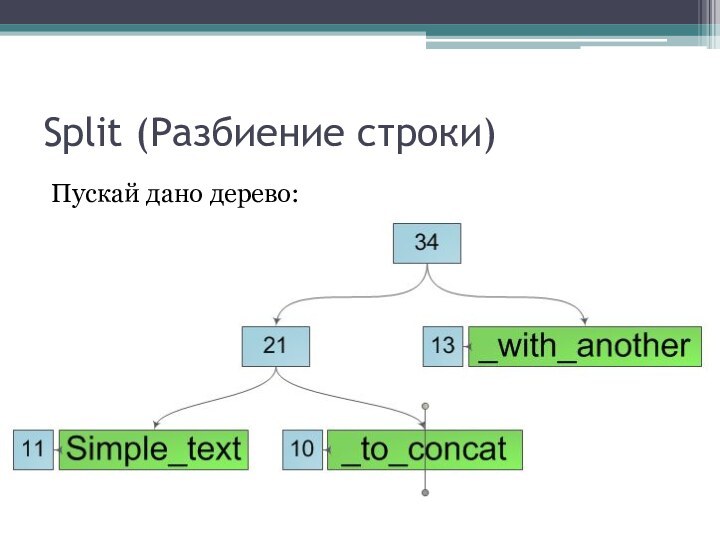
Split (Разбиение строки)
Пускай дано дерево:
Слайд 14
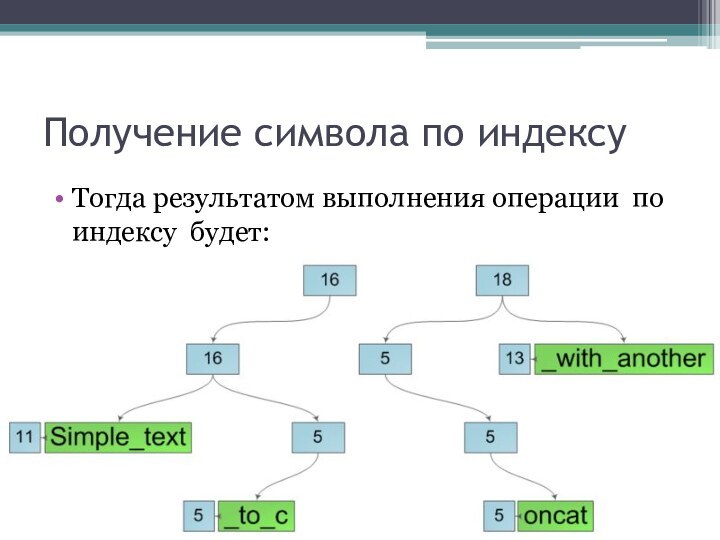
Получение символа по индексу
Тогда результатом выполнения операции по индексу будет:
Слайд 15
Возвращение функцией двух узлов
Для того, чтобы возвращать сразу
два узла, воспользуемся следующей структурой:
struct d_trie
{
struct trie *first;
struct trie
*second;
};
Слайд 16
Получение символа по индексу
struct d_trie *split(struct trie *node,
int i)
{
struct d_trie *res;
res = (d_trie*)malloc(sizeof(*res));
if (node == NULL)
return
NULL;
struct trie *tree1, *tree2;
tree1 = (trie*)malloc(sizeof(*tree1));
tree1->string = "";
tree1->length = 0;
tree1->left = NULL;
tree1->right = NULL;
tree2 = (trie*)malloc(sizeof(*tree2));
tree2->left = NULL;
tree2->right = NULL;
tree2->string = "";
tree2->length = 0;
Слайд 17
Получение символа по индексу
if (node->left != NULL)
if (node->left->length
>= i)
{
res = split(node->left, i);
tree1 = res->first;
tree2->left = res->second;
tree2->right
= node->right;
tree2->length = tree2->left->length + tree2->right->length;
}
else
{
res = split(node->right, i - node->left->length);
tree1->left = node->left;
tree1->right = res->first;
tree1->length = tree1->left->length + tree1->right->length;
tree2 = res->second;
}
Слайд 18
Операции удаления и вставки
Нетрудно понять, что имея операции merge и split,
можно легко через них выразить операции delete и insert по аналогии
с другими деревьями поиска.
Операция delete удаляет из строки подстроку начиная с индекса beginIndex и заканчивая (не включая) индексом endIndex.
Слайд 19
Операция удаления
struct trie *_delete(struct trie *node, int beginIndex,
int endIndex)
{
struct d_trie *res;
res = (d_trie*)malloc(sizeof(*res));
res = split(node, beginIndex);
struct
trie *tree3 = split(res->second, endIndex - beginIndex)->second;
return merge(res->first, tree3);
}