Слайд 2
Декларативная семантика программ на языке Пролог.
Язык Пролог
является не алгоритмическим,
а декларативным языком
программирования. Пролог⎯программа
лишь декларирует утверждения,
определяющие
свойства объектов и
отношения между ними, поэтому семантика
Пролог⎯программ является декларативной.
Слайд 3
Декларативная семантика программ на языке Пролог.
Декларативная семантика
программы
определяет, что истинно и при каких
значениях переменных. С точки
зрения
декларативной семантики, утверждения
программы являются формулами
исчисления предикатов 1-го порядка.
Слайд 4
Процедурная семантика программ на языке Пролог.
С другой
стороны, чтобы определить истинностные
значения вопроса, надо произвести вычисление
целей запроса,
поэтому логическая программа
имеет также процедурную семантику.
Процедурная семантика Пролог⎯программы
состоит в интерпретации входящих в программу
утверждений с точки зрения процесса установления
истинностных значений задаваемых в вопросе
утверждений.
Слайд 5
Процедурная семантика программ на языке Пролог.
Процедурная семантика
⎯ это
процедура вычисления списка целей на основе
заданной декларативной программы.
Слайд 6
Процедурная семантика программ на языке Пролог.
Назовем эту
процедуру именем «Вычислить».
Слайд 7
Процедурная семантика языка Пролог
определяет встроенные в Пролог⎯систему
механизмы логического
вывода. Рассмотрим
простейшие механизмы логического
вывода.
Процедурная семантика программ на языке
Пролог.
Слайд 8
Правило совпадения
Факты в программе не содержат
переменных, а вопрос
⎯ простой и
основной. В этом случае используется
правило совпадения: вопрос
выводим из
программы, если в программе имеется
совпадающий с вопросом факт.
Слайд 9
Правило обобщения факта
Факты в программе не содержат переменные,
а вопрос ⎯ простой и неосновной. В этом случае
для
вывода можно применить правило обобщения
факта: вопрос Q выводим из программы, если
найдется подстановкаθ, что вопрос Qθ выводим из
программы. Процедура поиска ответа на простой,
неосновной вопрос из программы, состоящей из
фактов без переменных, сводится к поиску факта,
являющегося примером вопроса.
Слайд 10
Правило обобщения факта
(Конкретизация переменных)
Побочным эффектом доказательства будет
конкретизация
переменных, входящих в
вопрос. Конкретизацией называется
присвоение переменной значения в
процессе выполнения
программы.
Слайд 11
Вычисление конъюнктивного запроса
Процедура поиска ответа на конъюнктивный,
неосновной вопрос
из программы, состоящей из
фактов без переменных, сводится к поиску
факта,
являющегося примером цели G1, а затем после
подстановки значений общих переменных в цель G2
производится поиск факта, являющегося примером
цели G2 данного вопроса. Если такой факт
обнаруживается, то выполняется конкретизация
переменных цели G2, которые не являются общими
с целью G1, и вычисление конъюнктивного вопроса
завершается успешно.
Слайд 12
SWI Prolog
Вычислительная модель языка Prolog
Слайд 13
Алгоритм унификации – основа вычислительной модели языка Пролог
Унификация (или сопоставление) —
основной шаг процесса вычисления запроса,
именно в
результате унификации
происходит конкретизация переменных и
обеспечивается продвижение к успешному
завершению логического вывода запроса.
Операндами операции унификации
являются логические термы.
Слайд 14
Правила унификации термов
Правило 1.
Если термы Т1 и Т2
— константы, то они
унифицируются только в том случае, когда
они
одинаковы. Целые и вещественные
числа сопоставимы только с равными им
числам. Атомы сопоставимы только с
идентичными атомами. Строки сопоставимы
с одинаковыми строками.
Слайд 15
Правила унификации термов
Правило 2.
Если терм Т1—константа или составной
терм,
а Т2 — неконкретизированная
переменная, не содержащаяся в Т1, то
Т1 и
Т2 унифицируются, причем в результате
переменная Т2 конкретизируется значением
Т1.
Слайд 16
Правила унификации термов
Правило 3.
Если термы Т1 и Т2
—
неконкретизированные переменные, то их
унификация успешна всегда, причем в
результате
унификации эти переменные
становятся сцепленными, то есть при
конкретизации одной из них, другая
одновременно конкретизируется тем же
значением.
Слайд 17
Правила унификации термов
Правило 4.
Если Т1 и Т2 ⎯составные
термы, то Т1 и Т2
унифицируются успешно, когда они имеют
одинаковые
главные функторы и арности, и
каждая пара соответствующих компонент
составных термов успешно унифицируется.
Слайд 18
Явная операция унификации
При выполнении логического вывода скрыто от
пользователя
выполняется большое число
операций унификации, обусловленных встроенным
в Пролог⎯систему алгоритмом логического
вывода.
Однако, у программиста имеется возможность
задать в качестве одной из целей явное выполнение
унификации двух термов с помощью операции
сопоставления ‘=’. Знак ‘\=’ является знаком
отрицания сопоставления.
Слайд 19
Примеры унификации термов
Пример 1.
?⎯2+1=1+2.
no
Составные термы 2+1 и 1+2
не
сопоставимы, и операция сопоставления
этих термов неуспешна.
Слайд 20
Примеры унификации термов
Пример 2.
?⎯2+1\=1+2.
yes
Операция отрицания сопоставления термов
2+1 и
1+2 успешна.
Слайд 21
Примеры унификации термов
Пример 2.
?⎯2+X=2+1.
X=1
yes
Операция сопоставления термов 2+X и
2+1
успешна.
Слайд 22
Общая схема согласования целевых утверждений.
Самым общим случаем Пролог⎯программы
является
программа, включающая как
факты, так и правила. Рассмотрим процесс
вычисления запроса
на основе такой
логической программы.
Слайд 23
Общая схема согласования целевых утверждений.
Процесс вычисления начинается с
некоторого
исходного вопроса Q, который в
общем случае может быть конъюнктивным,
и завершается получением одного из двух
результатов:
успешного согласования целей вопроса;
неуспеха (или неудачи).
Слайд 24
Общая схема согласования целевых утверждений (продолжение)
Допустим, что логическая
программа P
состоит из фактов и правил, а вопрос Q
⎯
конъюнктивный и содержит цели
G1,G2,…Gn. Интерпретатор языка Пролог
будет вычислять ответ на вопрос согласно
следующим принципам, на которых он
реализован.
Слайд 25
Общая схема согласования целевых утверждений (продолжение)
1) Цели запроса
обрабатываются слева направо, G1 будет согласовываться первой, а Gn
⎯последней.
Слайд 26
Общая схема согласования целевых утверждений (продолжение)
2) Предложения программы
просматриваются интерпретатором сверху вниз.
Слайд 27
Общая схема согласования целевых утверждений (продолжение)
3) Если цель
Gi сопоставима с заголовком правила Hj, то она должна
быть сопоставима с предикатами в правой части правила. Интерпретатор заменяет цель Gi на правую часть правила Hj. Это действие называется редукцией.
Слайд 28
Общая схема согласования целевых утверждений (продолжение)
Редукцией цели Gi
с помощью программы P называется замена цели Gi на
тело правила Cj, заголовок которого Hj унифицируется с целью Gi. Вычисление вопроса выполняется в виде последовательности редукций, цепочки преобразований исходного вопроса.
Слайд 29
Общая схема согласования целевых утверждений (продолжение)
На каждом этапе
вычисления существует
некоторая конъюнкция целей (или одна
цель), называемая резольвентой. Цели,
которые
добавляются в запрос в результате
редукции, называются производными
целями от цели Gi и правила Cj. Если цель
Gi сопоставима с заголовком правила Hj, то
список целей в запросе увеличивается.
Слайд 30
Общая схема согласования целевых утверждений (продолжение)
4) Если цель
Gi сопоставима с фактом, то конкретизируются переменные этой цели,
и общие переменные цели Gi и других целей, входящих в вопрос, затем осуществляется переход к сопоставлению следующей цели Gi+1 , и, таким образом, список целей, подлежащих согласованию уменьшается.
Слайд 31
Общая схема согласования целевых утверждений (продолжение)
5) Когда мы
таким образом достигнем последней цели в запросе, и она
успешно будет согласована с каким-либо фактом программы, то текущая резольвента окажется пустой, и вычисление запроса будет успешным.
Слайд 32
Пример вычисления запроса на основе программы, включающей и
факты, и правила.
Пусть программа содержит утверждения,
приведенные ниже:
big(‘медведь’). %предложение 1
big(‘слон’). %предложение
2
little(‘кот’). %предложение 3
little(‘мышь’). %предложение 4
black(‘кот’). %предложение 5
grey(‘слон’). %предложение 6
grey(‘мышь’). %предложение 7
brown(‘медведь’). %предложение 8
dark(Z):⎯black(Z). %предложение 9
dark(Z):⎯brown(Z). %предложение 10
Слайд 33
Шаг 1 вычисления запроса
Для вычисления запроса “? ⎯
dark(X),big(X). “ интерпретатор выполняется следующие действия:
Текущая резольвента Q1 есть
исходный запрос ⎯ dark(X),big(X).
Шаг 1. Текущая резольвента Q2 является конъюнкцией целей dark(X),big(X). Выбираем первую цель G21⎯dark(X) и, просматривая программу с первого предложения, находим предложение 9, сопоставимое с целью G21, является правилом
dark(Z):⎯black(Z).
переименовываем переменную Z на Х и вместо цели G21 подставляем правую часть правила 9. Получаем текущую резольвенту Q2⎯black(X),big(X)
Слайд 34
Шаг 2 вычисления запроса
Шаг 2. Текущая резольвента Q2 является
конъюнкцией целей black(X),big(X). Выбираем первую цель G21⎯black(X) и, просматривая
программу с первого предложения, находим предложение 5, сопоставимое с целью G21, black(‘кот’).
при подстановке {X=’кот’}. Предложение 5 является фактом, поэтому список целей в резольвенте сократится, так как цель G21 удаляется , а в цель G22 при подстановке {X=’кот’} примет вид
big(‘кот’).
Получаем текущую резольвенту Q3: big(‘кот’).
Слайд 35
Шаг 3 вычисления запроса
Шаг 3. Текущая резольвента Q3 включает
одну цель G31
big(‘кот’).
Просматривая программу с первого
предложения, не
находим ни одного
предложения, сопоставимого с целью G31,
поэтому выполняется возврат на шаг 2.
Слайд 36
Шаг 4 вычисления запроса
Шаг 4. Текущая резольвента Q4=Q2 является
конъюнкцией целей black(X),big(X). Выбираем первую цель G41⎯black(X) и, просматривая
программу с предложения 6 до конца программы, и не находим ни одного предложения, сопоставимого с целью G41, поэтому выполняется возврат на шаг 1.
Слайд 37
Шаг 5 вычисления запроса
Шаг 5. Текущая резольвента Q5=Q1 является
конъюнкцией целей dark(X),big(X). Выбираем первую цель G51⎯dark(X) и, просматривая
программу с предложения 10, находим предложение 10, сопоставимое с целью G21, является правилом
dark(Z):⎯brown(Z).
переименовываем переменную Z на Х и вместо цели G21 подставляем правую часть правила 9. Получаем текущую резольвенту Q5 ⎯
brown (X),big(X).
Слайд 38
Шаг 6 вычисления запроса
Шаг 6. Текущая резольвента Q5
является конъюнкцией целей brown(X),big(X). Выбираем первую цель G51⎯ brown(X)
и, просматривая программу с первого предложения, находим предложение 8, сопоставимое с целью G51, brown(‘медведь’).
при подстановке {X=’медведь’}. Предложение 8 является фактом, поэтому список целей в резольвенте сократится, так как цель G51 удаляется , а в цель G52 при подстановке {X=’медведь’} примет вид
big(‘медведь’). Получаем текущую резольвенту Q6: big(‘медведь’).
Слайд 39
Шаг 7 вычисления запроса
Шаг 7. Текущая резольвента Q6
включает одну цель G61 big(‘медведь’). Просматривая программу с первого
предложения, находим предложение 1, сопоставимое с целью G61,
которое является фактом, поэтому цель G61 удаляется из текущей резольвенты, и она становится пустой, Q7=•.
Текущая резольвента Q7 есть пустой дизъюнкт, это указывает на успешное завершение вычисления запроса Q1. Интерпретатор выдает конкретизацию переменной {X=’медведь’} как результат вычисления запроса.
Слайд 40
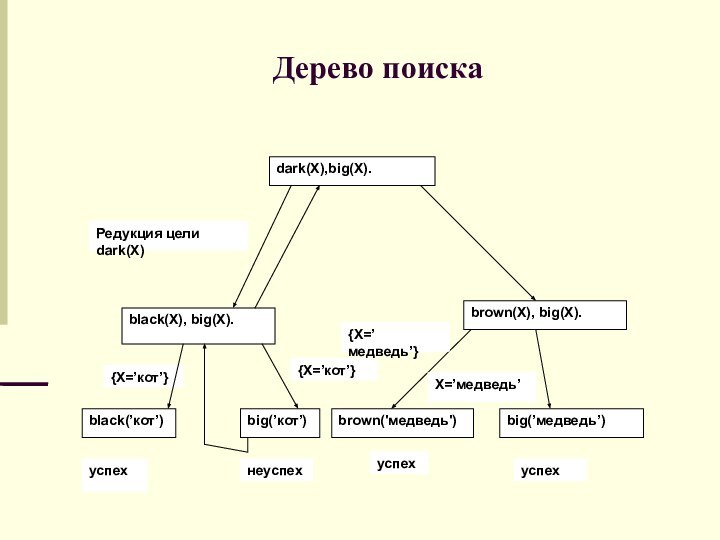
Дерево поиска
Процесс вычисления запроса удобно представить в
виде дерева поиска. Дерево поиска ответа на любой запрос
строится следующим образом.
Корнем дерева является исходный вопрос Q.
Вершины дерева соответствуют целям (резольвентам), которые в общем случае являются конъюнктивными. В каждой выделяется одна цель.
Слайд 41
Дерево поиска
Для каждого утверждения программы, заголовок которого
унифицируется с выделенной в вершине целью имеется ребро, выходящее
из этой вершины.
На ребрах дерева записываются подстановки, которые образуются в результате унификации выделенной в вершине цели и утверждения.
Слайд 42
Дерево поиска
Лист дерева называется успешной вершиной, если
существует подстановка, удовлетворяющая последнюю цель в списке целей. Лист
дерева называется безуспешной вершиной, если нет в программе утверждений, которые сопоставимы с выделенной в вершине целью.
dark(X),big(X).
Редукция цели dark(X)
black(X), big(X).
black(’кот’)
{X=’кот’}
big(’кот’)
{X=’кот’}
неуспех
brown(X), big(X).
brown('медведь')
{X=’медведь’}
успех
успех
big(’медведь’)
X=’медведь’
успех
Слайд 44
Механизм автоматического возврата (backtracing)
Когда выполнение программы достигает
тупиковой вершины
отмеченной словом
"неуспех", автоматически происходит
возврат на предыдущий уровень дерева
поиска, так
как в Пролог⎯систему встроен
механизм возврата (backtracing).
Слайд 45
Механизм автоматического возврата (backtracing)
Выполнение алгоритм поиска решения можно
представить
как обход лабиринта, где на каждой
развилке приходится выбирать новый
путь. При
попадании в тупик, т.е. на безуспешную вершину
(лист дерева поиска), надо следовать в обратном
направлении до первого перекрестка, и выбирать
другой не опробованный путь.
Процесс продолжается до тех пор, пока не
встретится успешная вершина или будут
пройдены все пути дерева поиска.
Слайд 46
Механизм автоматического возврата (backtracing). Понятие маркера.
Для того, чтобы
представить работу
механизма автоматического возврата
удобно воспользоваться понятием маркера.
Маркер отмечает текущее
утверждение в
программе, сопоставимое с целью.
Слайд 47
Механизм автоматического возврата (backtracing). Понятие маркера.
Для каждой цели
в запросе Пролог⎯система
создает свой собственный маркер, который
будем обозначать значком
“∇”. Маркеры
могут передвигаться только вперед.
Однако, когда цель начинает
согласовываться сначала, соответствующий
маркер устанавливается на первое
утверждение, заголовок которого совпадает
с именем предиката ⎯ цели.
Слайд 48
Пример поиска решений с возвратом.
Пусть программа «Однокурсники»
содержит следующие утверждения:
student_course(X,Y):⎯student(X,K1), student(Y,K2),X\=Y,K1=K2.
student(‘Иванов’,1).
student(‘Петров’,4).
student(‘Сидоров’,2).
student(‘Кузнецов’,4).
Пусть требуется согласовать запрос:
?⎯ student_course(X,Y).
Слайд 49
Пример поиска решений с возвратом.
Пусть требуется согласовать
запрос:
?⎯ student_course(X,Y).
Этот запрос сопоставим с первым утверждением,
которое является
правилом, поэтому производится
редукция цели, и текущая резольвента примет вид:
ТР: student(X,K1), student(Y,K2),X\=Y,K1=K2.
Создадим маркер ∇1 для первой цели в
резольвенте student(X,K1) и маркер ∇2 для второй
цели в резольвенте student(Y,K2).
Слайд 50
Поиск первого решения
При просмотре фактов student в программе
маркеры будут передвигаться следующим образом:
(2) student(‘Иванов’,1). ∇1 ↓∇2 (no) ↓∇2 (no)
(3) student(‘Петров’,4). ↓∇2 (no) ∇1 ↓∇2 (no)
(4) student(‘Сидоров’,2). ↓∇2
(no) ↓∇2 (no)
(5) student(‘Кузнецов’,4). ↓∇2 (no) ↓∇2 (yes)
возврат 1-й цели успешный
вывод
при подстановке {X=‘Петров’; Y=‘Кузнецов’}.
Таким образом, ответ на запрос будет выдан в следующем виде:
?⎯ student_course(X,Y).
X=‘Петров’
Y=‘Кузнецов’⎯ >