Слайд 2
Теория устойчивости
Запишем уравнение равновесия конструкции, к которой приложена
система постоянных сил, в следующем виде:
[ K ] { u } = { P }
Рассмотрим эффект дифференциальной (геометрической) жесткости. Дифференциальная жесткость [ Kd ] появляется в результате учета членов высокого порядка в зависимостях деформация-перемещение. Эти зависимости подразумевают, что перемещения в конструкции не зависят от интенсивности нагрузки.
Слайд 3
Теория устойчивости (продолжение)
Пусть λ произвольный скалярный множитель для
другой "интенсивности" нагрузки.
При нагружении конструкции данной силой с различной
интенсивностью, могут быть найдены несколько положений неустойчивого равновесия. Эти положения равновесия являются решениями задачи на собственные значения.
Слайд 4
Решение задачи на собственные значения
[
K – λKd ] {φ} = 0 (1)
Решение нетривиально (отлично от нуля) только для определенных значений λ = λi для i = 1, 2, 3,…, n
которые делают матрицу [ K – λKd ] сингулярной.
Слайд 5
Решение задачи на собственные значения (продолжение)
Каждому собственному значению
λi, соответствует единственный собственный вектор { φi }.
{
φi } может быть масштабирован с помощью любого скалярного множителя и по прежнему оставаться решением уравнения (1).
Компоненты вектора { φi } - вещественные числа..
Слайд 6
Последовательности решений для задач устойчивости
SOL 105 Линейная устойчивость
SOL 106 Нелинейная
устойчивость
Ограничения для SOL 105
Требования к конструкции до потери устойчивости:
Перемещения должны быть малы.
Напряжения должны быть в упругой области (и линейно зависеть от деформаций).
Слайд 7
Последовательности решений для задач устойчивости (продолжение)
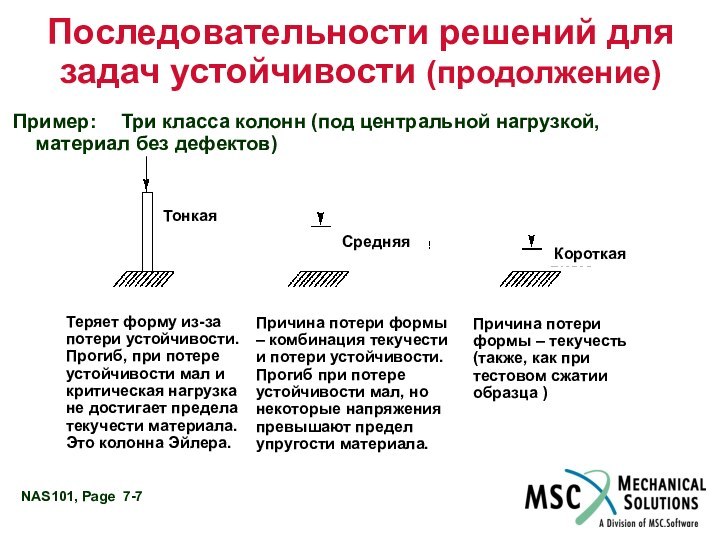
Пример: Три класса колонн
(под центральной нагрузкой, материал без дефектов)
Тонкая
Средняя
Короткая
Теряет форму из-за потери
устойчивости. Прогиб, при потере устойчивости мал и критическая нагрузка не достигает предела текучести материала. Это колонна Эйлера.
Причина потери формы – комбинация текучести и потери устойчивости. Прогиб при потере устойчивости мал, но некоторые напряжения превышают предел упругости материала.
Причина потери формы – текучесть (также, как при тестовом сжатии образца )
Слайд 8
Последовательности решений для задач устойчивости (продолжение)
Примечание: SOL 105
может применяться для конструкций с небольшими дефектами материала или
с очень малым эксцентриситетом нагрузки (например, когда нагрузка направлена не строго в центр и приводит к небольшому изгибу). Здесь инженеру надо исходить из здравого смысла.
Те же соображения применимы при анализе пластин.
Слайд 9
Примеры нелинейного анализа устойчивости
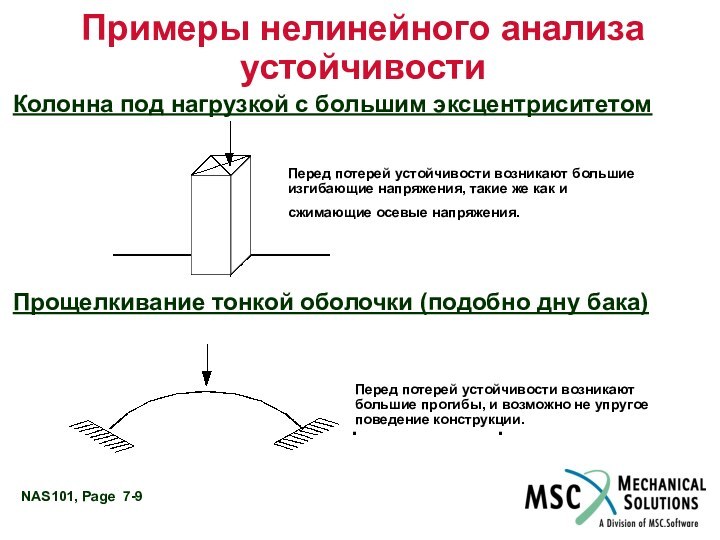
Колонна под нагрузкой с большим
эксцентриситетом
Прощелкивание тонкой оболочки (подобно дну бака)
Перед потерей устойчивости
возникают большие изгибающие напряжения, такие же как и сжимающие осевые напряжения.
Перед потерей устойчивости возникают большие прогибы, и возможно не упругое поведение конструкции.
Слайд 10
Правила для анализа устойчивости SOL 105
(Для справки необходимо
смотреть раздел 13, MSC/NASTRAN Linear Statics Users Guide)
Секция CASE
CONTROL должна содержать не менее двух SUBCASE.
Запросы на вывод, которые относятся только к решению статической задачи должны быть помещены в первом SUBCASE.
METHOD должен появиться в отдельном SUBCASE для выбора записей EIGB или EIGRL из секции BULK DATA для решения задач устойчивости.
Если имеется несколько статических решений, тогда используйте команду STATSUB для выбора варианта одного из статических решений для дальнейшего решения задачи устойчивости.
Слайд 11
Правила для анализа устойчивости SOL 105 (продолжение)
Если необходимо,
могут использоваться различные условия в SPC узлах в SUBCASE
статического решения и SUBCASE решения задачи устойчивости.
Запросы на вывод могут быть помещены в любом выбранном SUBCASE.
Запросы на вывод, действующие одновременно и в статическом расчете и в анализе устойчивости могут быть помещены выше уровня SUBCASE.
Слайд 12
Записи для линейного анализа устойчивости
Секция EXECUTIVE CONTROL
SOL 105
Секция CASE CONTROL
Слайд 13
Записи для линейного анализа устойчивости (продолжение)
Секция CASE CONTROL
должна содержать не менее двух SUBCASE.
Секция BULK DATA
Определение
условий статического нагружения
EIGB Данные для нахождения собственного значения
или
EIGRL Данные для нахождения собственного значения по методу Ланцоша.
Слайд 14
Запись EIGRL
EIGRL Рекомендуемая запись для расчета устойчивости
Определяет
данные, необходимые для проведения решения задачи на собственные значения
и анализа устойчивости методом Ланцоша.
Слайд 15
Запись EIGRL (продолжение)
Поле Содержание
SID Идентификатор набора (уникальное целое число >
0)
V1, V2 Анализ вибрации: диапазон интересующих частот
Анализ устойчивости: диапазон интересующих
λ
ND Число необходимых корней (целое > 0 или оставлять чистым)
MSGLVL Уровень диагностики (целое, от 0 до 3 или оставлять чистым)
MAXSET Число векторов в блоке (целое, от 1 до 15 или оставлять чистым)
Слайд 16
Пример - простая колонна Эйлера
Задача
Найти критическую нагрузку и
соответствующую ей первую форму потери устойчивости цилиндрического стержня.
21 дюйм
Свободно
Зафиксировано
Круглое
сечение
Диаметр = 0.25 дюйма
E = 30.E+6 фунтов/дюйм2
I = 1.917E-4 дюйм4
Площадь = 4.909E-2 дюйм2
Слайд 17
Пример - простая колонна Эйлера (продолжение)
Теоретическое решение
где Leff =
эффективная длина колонны
= 2L для свободно опертой колонны
Слайд 18
Пример - простая колонна Эйлера (продолжение)
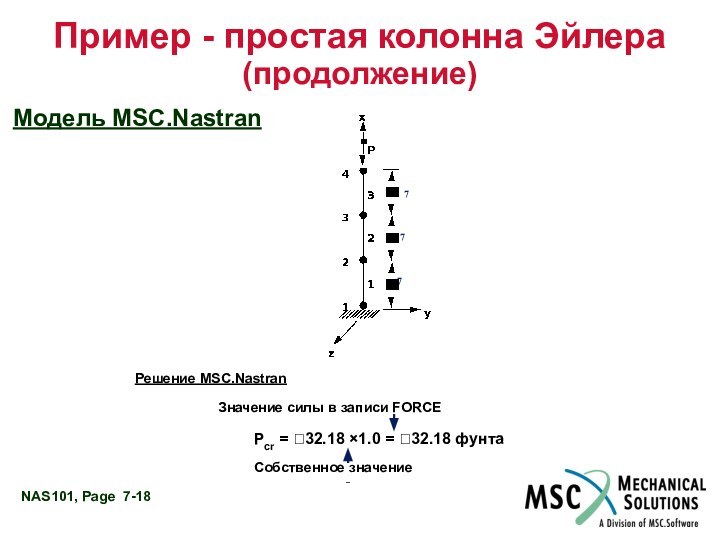
Модель MSC.Nastran
7
7
7
Решение MSC.Nastran
Значение силы в записи FORCE
Pcr = 32.18 ×1.0 =
32.18 фунта
Собственное значение
Слайд 19
Пример - простая колонна Эйлера – входной
файл
Слайд 20
Пример - простая колонна Эйлера – выходной
файл
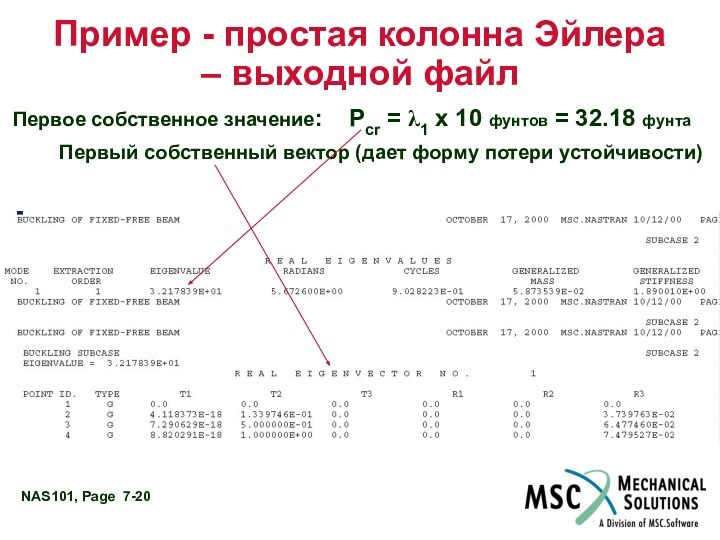
Первое собственное значение: Pcr = λ1 x 10
фунтов = 32.18 фунта
Первый собственный вектор (дает форму потери устойчивости)
Слайд 21
Литература по анализу устойчивости
MSC Seminar Notes, “MSC/NASTRAN
Material and Geometric Nonlinear Analysis”:
MSC.Nastran Linear Static Analysis Users
Guide, Section 13.
MSC.Nastran Verification Problem Manual (Version 64, January 1986 Edition):
Problem 3.0501A, “Lateral Buckling of a Cantilever Beam”
Problem 3.0502A, “Simple Frame Analysis with Buckling”
Problem 3.7701S, “Euler Buckling of a Simply Supported Beam”
Слайд 22
Литература по анализу устойчивости (продолжение)
MSC.Nastran Demonstration Problem Manual
(Version 64, March 1985 Edition):
Under Elastic Stability Analysis, see
Demonstration Problem D0504A, “Flexural Buckling of a Beam”
MSC.Nastran Application Notes
October 1978 “Buckling and Real Eigenvalue Analysis of Laminated Plates”
September 1979 “Static Stability of Structures with Nonlinear Differential Stiffness”
February 1982 “Elastic-Plastic Buckling of a Thin Spherical Shell”
November 1985 “Nonlinear Buckling Analysis”
Слайд 23
Пример 9
Анализ устойчивости пластины
Слайд 24
Пример 9 (продолжение)
Описание модели
Та же самая модель панели
что и в Примере 5, без подкреплений.
В этой
модели применены следующие граничные условия:
Опирание на левом конце
“Ролики” на правом конце
Нулевые вертикальные перемещения на верхней и нижней гранях
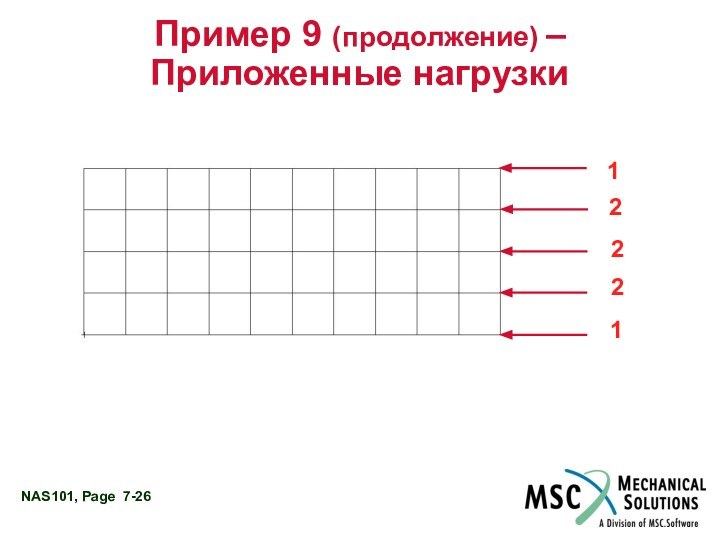
Приложим 100 фунт/дюйм2 сжимающие нагрузки к правому краю пластины
Общая нагрузка на правой стороне = (100) (8) (.01) = 8
Приложите 1 фунт в каждый из узлов 11 и 55 сетки
Приложите 2 фунта в каждый из узлов 22, 33 и 44 сетки
Слайд 25
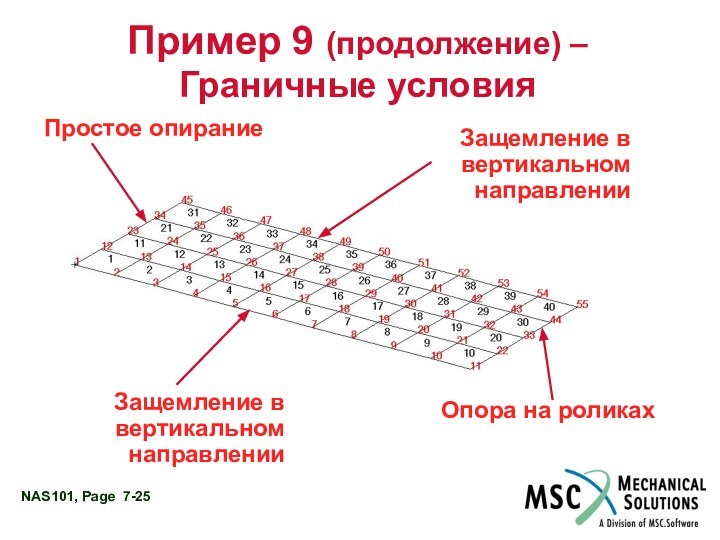
Пример 9 (продолжение) – Граничные условия
Простое опирание
Опора
на роликах
Защемление в вертикальном направлении
Защемление в вертикальном направлении