Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Системы счисления

Содержание

2. Система счисления – это совокупность приемов и
3. Непозиционная система счисления – это система счисления,
4. Арифметика каменного векаЕдиничная (унарная)система счисления10 - 11
5. Древнегреческая нумерацияВ V веке до н.э. появилась алфавитная нумерация.Пример:
6. Славянская кириллическая нумерацияПример:
7. Египетская нумерация1 10
8. Примером непозиционной системы счисления, которая сохранилась до
9. Римская система счисленияПример:DC-XV=DLXXXVЧтобы записать число, римляне использовали не только сложение, но и вычитание.
10. В старину на Руси среди простого народа
11. Система счисления называется позиционной, если количественные значения
12. В данной системе счисления используется десять различных
13. Другие позиционные системы счисленияШирокое распространения в первой
14. Позиционные системы счисленияОсновная характеристика позиционной СС основание
15. Система счисленияОснованиеАлфавит цифрДесятичнаяДвоичнаяВосьмеричнаяШестнадцатеричная 102 8 160,1,2,3,4,5,6,7,8,90,10,1,2,3,4,5,6,70,1,2,3,4,5,6,7,8,9, А(10),В(11),С(12), D(13),Е(14),F(15)Позиционные системы счисления
16. Перевод целых чисел из десятичной системы счисления17282221000142Пример:
17. Скачать презентацию
18. Похожие презентации

Система счисления – это совокупность приемов и правил для обозначения и именования чисел. Знаки, используемые при записи чисел, называются цифрами. Системы счисленияпозиционныенепозиционные

Непозиционная система счисления – это система счисления, в которой количественные значения символов,

Арифметика каменного векаЕдиничная (унарная)система счисления10 - 11 тыс. лет до н. э.

Древнегреческая нумерацияВ V веке до н.э. появилась алфавитная нумерация.Пример:

Славянская кириллическая нумерацияПример:

Примером непозиционной системы счисления, которая сохранилась до наших дней, может служить система

Римская система счисленияПример:DC-XV=DLXXXVЧтобы записать число, римляне использовали не только сложение, но и вычитание.

В старину на Руси среди простого народа широко применялись системы счисления, отдаленно

Система счисления называется позиционной, если количественные значения символов, используемых для записи чисел,

В данной системе счисления используется десять различных знаков (0, 1, 2, 3,

Другие позиционные системы счисленияШирокое распространения в первой трети XX века имели элементы

Позиционные системы счисленияОсновная характеристика позиционной СС основание – количество цифр, используемое для

Система счисленияОснованиеАлфавит цифрДесятичнаяДвоичнаяВосьмеричнаяШестнадцатеричная 102 8 160,1,2,3,4,5,6,7,8,90,10,1,2,3,4,5,6,70,1,2,3,4,5,6,7,8,9, А(10),В(11),С(12), D(13),Е(14),F(15)Позиционные системы счисления

Перевод целых чисел из десятичной системы счисления17282221000142Пример: 1710

Сложение 0+0=0 0+1=1 1+0=1 1+1=10 3. Умножение0•0=01•0=00•1=01•1=1Арифметика с двоичными числами 2. Вычитание

Слайды презентации

Слайд 2 Система счисления – это совокупность приемов и правил

Система счисления – это совокупность приемов и правил для обозначения и

для обозначения и именования чисел. Знаки, используемые при записи

чисел, называются цифрами.

Системы счисления

позиционные

непозиционные

Слайд 3 Непозиционная система счисления – это система счисления, в

Непозиционная система счисления – это система счисления, в которой количественные значения

которой количественные значения символов, используемых для записи чисел, не

зависят от их положения.

Слайд 4 Арифметика каменного века

Единичная (унарная)
система счисления
10 - 11 тыс.

Арифметика каменного векаЕдиничная (унарная)система счисления10 - 11 тыс. лет до н.

лет до н. э.

любое число образуется путем повторения

одного знака, символизирующего единицу.

Слайд 5 Древнегреческая нумерация
В V веке до н.э. появилась алфавитная

нумерация.
Пример:

Слайд 6 Славянская кириллическая нумерация
Пример:

Слайд 7 Египетская нумерация
1 10

100

1000

10000 100000 1000000 10000000

5000 лет тому назад

= 90

Пример:

Слайд 8 Примером непозиционной системы счисления, которая сохранилась до наших

дней, может служить система счисления, применявшаяся более двух с

половиной тысяч лет назад в Древнем Риме.

Римская система счисления

Слайд 9 Римская система счисления
Пример:
DC-XV=DLXXXV
Чтобы записать число, римляне использовали не

только сложение, но и вычитание.

Слайд 10 В старину на Руси среди простого народа широко

В старину на Руси среди простого народа широко применялись системы счисления,

применялись системы счисления, отдаленно напоминающих римскую. С их помощью

сборщики податей заполняли квитанцию об уплате подати – ясака и делали записи в податной тетради.

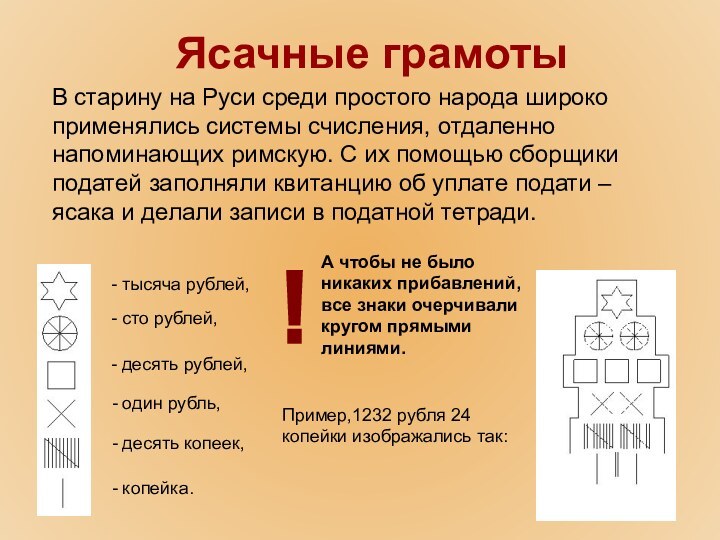
А чтобы не было никаких прибавлений, все знаки очерчивали кругом прямыми линиями.

Пример,1232 рубля 24 копейки изображались так:

Ясачные грамоты

Слайд 11 Система счисления называется позиционной, если количественные значения символов,

Система счисления называется позиционной, если количественные значения символов, используемых для записи

используемых для записи чисел, зависят от их положения (места,

позиции) в записи числа

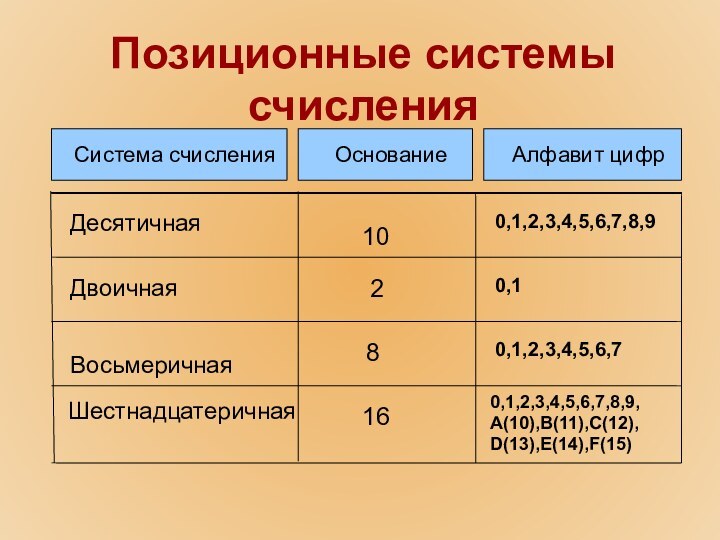
Позиционные системы счисления

Слайд 12 В данной системе счисления используется десять различных знаков

В данной системе счисления используется десять различных знаков (0, 1, 2,

(0, 1, 2, 3, 4, 5, 6, 7, 8,

9).

Потребовалось много тысячелетий, чтобы люди научились называть и записывать числа так, как это делаем мы с вами. Начало этому было положено в Древнем Египте и Вавилоне. Получив название арабской, эта система распространилась по всей Европе и быстро вытеснила остальные системы.

Десятичная система счисления

Слайд 13 Другие позиционные системы счисления
Широкое распространения в первой трети

Другие позиционные системы счисленияШирокое распространения в первой трети XX века имели

XX века имели элементы двенадцатеричной системы счисления. Число 12

имеет больше делителей, чем 10 – поэтому в двенадцатеричной системе производить расчеты удобнее, чем в десятичной. И только возможность счета по пальцам рук склонила чашу весов на сторону числа 10. Тем не менее, дюжина вошла прочно в нашу жизнь: карандашей и фломастеров в наборе 6, 12 или 24; чайные и столовые сервизы бывают на 6 или на 12 персон; комплект носовых платков – 12 штук.

А вот шведский король Карл XII увлекался восьмеричной системой, считал ее более удобной и намеревался ввести ее как общегосударственную. Только неожиданная смерть короля помешала осуществлению столь необычного намерения.

Слайд 14 Позиционные системы счисления
Основная характеристика позиционной СС основание –

Позиционные системы счисленияОсновная характеристика позиционной СС основание – количество цифр, используемое

количество цифр, используемое для представления чисел
Основанием может быть любое

натуральное число.
Обозначение:
10112, 2810, 1038, ...

Слайд 15 Система счисления
Основание
Алфавит цифр
Десятичная
Двоичная
Восьмеричная
Шестнадцатеричная
10
2
8
16
0,1,2,3,4,5,6,7,8,9
0,1
0,1,2,3,4,5,6,7
0,1,2,3,4,5,6,7,8,9, А(10),В(11),С(12), D(13),Е(14),F(15)
Позиционные

системы счисления

Слайд 16 Перевод целых чисел из десятичной системы счисления
17
2
8
2
2
2
1
0
0
0
1
4
2
Пример: 1710

Х2
Ответ:

1710 100012

Алгоритм перевода:

1. Последовательно выполнять деление данного числа и получаемых неполных частных на основание новой системы счисления (т.е. на р) до тех пор, пока получим неполное частное, меньше делителя;

2. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;

3. Составить число в новой системе счисления, записывая его, начиная с последнего частного и все полученные остатки в обратном порядке.