Презентация на тему Системы счисления

это величина, а не символьная

Цифры – набор символов, участвующих в записи числа.

системы счисления

каждой цифре соответствует величина, не зависящая от ее места в записи числа

величина числа зависит
от номера позиции
цифры при его записи

– способ записи чисел,

а также арифметических действий с ними.

352, 23

VII, XIX

Алфавит – совокупность различных цифр, используемых для записи чисел.

лет до н.э.
2,5 тысяч лет до н.э.

- единицы

- десятки

- сотни

= 3 4 5

непозиционные системы счисления

или

см. пример

единицы
- десятки
= 33
непозиционные системы счисления
цифры:
и
- 60
;

; 603

; … ; 60n

2-ой
разряд

1-ый
разряд

= 60 + 20 + 2 = 82

пример

3600 + 30 + 2 = 3632
Шестидесятеричная вавилонская

=

!

из значений
цифр и групп

Группа 1-го вида - несколько одинаковых
подряд идущих цифр: XX = 20

Группа 2-го вида - разность значений
двух цифр, если слева стоит меньшая:
СМ = 1000 – 100 = 900

Цифры:

D X L I I

= 542

X X X I I

= 32

Число формировалось из цифр, а также с помощью групп:

500 лет до н.э.

+ 4
4 4 4 =
C D X L

M C M L X X I V =

1 9 7 4

1000 +

(M-C) = 1000 - 100 = 900 +

50 +

20 +

4

(D-C)

+ (L-X)

+ (V-I)

400

40

4

год 6367. Варяги из заморья
взимали дань…»
- тысячи
- тьма:

100 000 - легион

1000 000 - леодр

1050 - колода

(«Повесть временных лет»)

. . .

= 10 000

«более сего несть человеческому уму разумевати»

- титло

«Аз»

«Веди»

«Глаголь»

«Добро»

«Есть»

«Зело»

«Земля»

«Иже»

«Фита»

«И»

понятиями
«цифра» и «число»?
Какие следы разных
систем счисления

? ? ?

в виде последовательности цифр, количественное значение которых зависит от

позиционные системы счисления

Базис позиционной системы счисления – это последовательность чисел, каждое из которых задает значение цифры «по месту» и «вес» каждого разряда.

Десятичная система: 1, 10, 102, 103, … , 10n

Двоичная система: 1, 2, 22, 23, … , 2n

P-ичная система: …, p-n, …, p-2, p-1, p0, p1 , … , pn

p – основание системы

1 2 3 5

1 позиция

2 позиция

3 позиция

4 позиция

х 1

х 10

х 100

х 1000

1000 100 10 1
(103) (102) (101) (100)

25310
Десятичная система
Базис: …, 10-2, 10-1, 1, 101, 102,

Основание: 10

Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Нетрадиционные

Фибоначчиевая система

Базис: 1, 2, 3, 5, 8, 13, 21, 34, 55, …

Алфавит: 0, 1

Пример: 10000100ф = 3 + 34 =3710

Смешанные: P-Q-ичные

Каждая цифра числа, заданного в Q-ичной системе,
заменяется ее представлением в P-ичной системе.

Двоично-десятичная система

3580910 = 0011 0101 1000 0000 10012-10

?

Почему в записи числа в фибоначчиевой системе не могут стоять две единицы подряд?

1,

Базис системы – геометрическая прогрессия с основанием p:
…, p-2, p-1, p0, p1, p2, p3, p4, p5, …

позиционной системе счисления число равно сумме степеней

позиционные системы счисления

X = anPn + an-1Pn-1 + … +a1P + a0 + b-1P-1 + b-2P-2 + … + b-kP-k + …

Xp = an…a1a0, b-1…b-k...P

= 1102 + 4 101+7 100+2 10-1 + 0 10-2 + 5 10-3

Арифметические действия над числами во всех P-ичных системах счисления выполняются одинаково.

!

( +    )

147,205

147,20510 = 1100 + 4 10 + 7 1 + 2  0,1 + 0  0,01 + 5  0,001 =

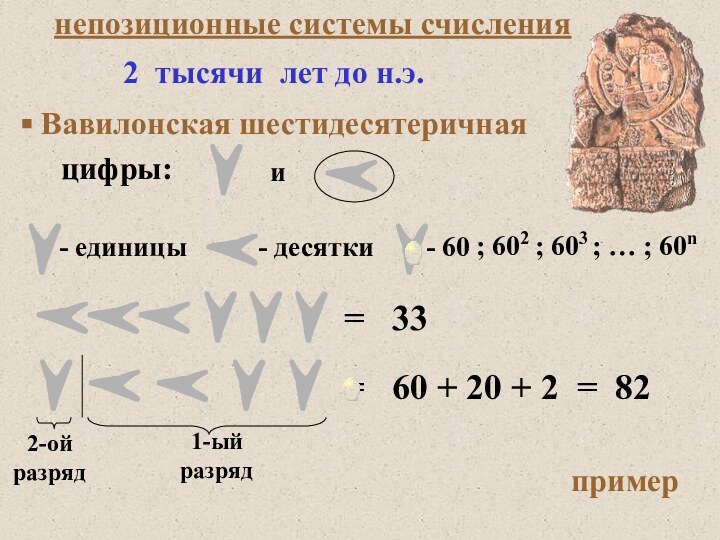
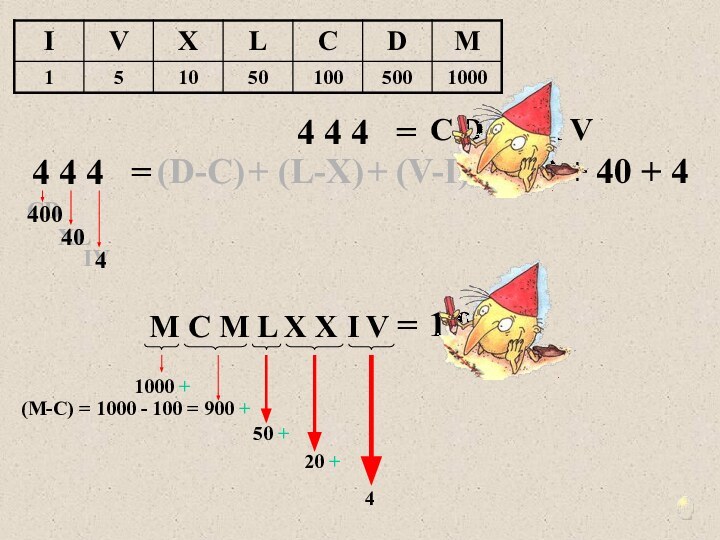
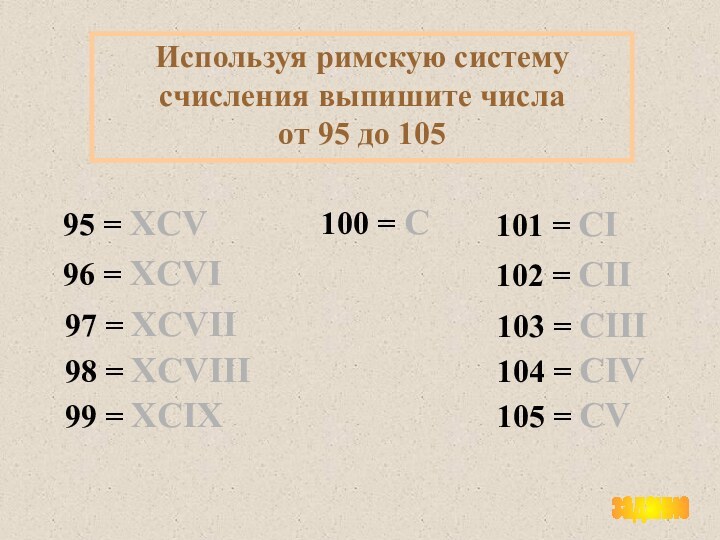
алфавит
Лейбниц (Leibniz) Готфрид Вильгельм
(1646-1716)
немецкий философ, математик, физик,

Лейбниц, изрядное время уделивший двоичной (бинарной) математике, видел в ней
«… прообраз творения».
Он считал, что «единица представляет божественное начало, а ноль – небытие. Высшее Существо создает все сущее из небытия точно таким же образом, как единица с помощью нуля выражает все числа».

1 0 1 0 0 12 = 120 + 021 + 022 + 123 + 024 + 125 = 1 + 8 + 32 = 4110

20

21

22

23

24

25

1

20

0

21

0

22

1

23

0

24

1

25

0 1

и

задание:

1001012 =

1010102 =

1 + 021 + 122 + 023 + 024 + 125 = 1 + 4 + 32 = 3710

0 + 121 + 022 + 123 + 024 + 125 = 2 + 8 + 32 = 4210

Перевод из двоичной системы счисления в десятичную:

см. слайд

С конца ХХ века, века компьютеризации, человечество пользуется двоичной системой ежедневно, так как вся информация, обрабатываемая ЭВМ, хранится в них в двоичном виде.

…, ¼, ½, 1, 2, 4, 8, 16, 32, … – базис
(…, 2-2, 2-1, 20, 21, 22, 23, 24, 25, …)

– основание системы
0, 1 – алфавит
0

и

Перевод из десятичной системы счисления в двоичную:

51 : 2 = 25

1

25 : 2 = 12

1

12 : 2 = 6

0

6 : 2 = 3

0

3 : 2 = 1

1

остаток

5110 =

1

1 1 0 0 1 1 2

1

0

0

1

1

76 : 2 = 38 0
38 : 2 = 19 0
19 : 2 = 9 1
9 : 2 = 4 1
4 : 2 = 2 0
2 : 2 = 1 0

7610 =

76

1

0

0

1

1

0

0

2

задание:

16810 =

24110 =

7710 =

проверка:

168 : 2 = 84 0
84 : 2 = 42 0
42 : 2 = 21 0
21 : 2 = 10 1
10 : 2 = 5 0
5 : 2 = 2 1
2 : 2 = 1 0

остаток

остаток

16810 = 101010002

101010002

111100012

241 : 2 = 120 1
120 : 2 = 60 0
60 : 2 = 30 0
30 : 2 = 15 0
15 : 2 = 7 1
7 : 2 = 3 1
3 : 2 = 1 1

24110 = 111100012

10011012

77 : 2 = 38 1
38 : 2 = 19 0
19 : 2 = 9 1
9 : 2 = 4 1
4 : 2 = 2 0
2 : 2 = 1 0

7710 = 10011012

в сто первый класс ходила,
( 101 )
В портфеле

( 100 )

Всё это правда, а не бред.

Когда, пыля десятком ног,

( 10 )

Она шагала по дороге,

За ней всегда бежал щенок

С одним хвостом, зато стоногий.

( 100 )

Она ловила каждый звук

Своими десятью ушами,

( 10 )

И десять загорелых рук

Портфель и поводок держали.

Рассматривали мир привычно…

И десять темно-синих глаз

( 10 )

Но станет всё совсем обычным,

Когда поймете вы рассказ.

( 10 )

( 1 )

X X I I
колода
традиционные

нетрадиционные

смешанные

0011 0101 2-10

10001010Ф

1000100112

задание

до 105
задание
100 = C

представить в виде суммы степеней

задание

Ответ: да.

Ответ: 111112 = 3110.

разрезали пополам, стало 110 половинок.
Возможно ли это? Обоснуйте

задание

Ответ: да, если считать числа в задаче представленными в двоичной системе счисления:
112=120 + 121=310;
1102 = 020 + 121 + 122 = 2 + 4 = 610

а)

задание

Ответ: четное число в двоичной системе счисления оканчивается на 0, а нечетное – на 1.
а) 1012 = 510 ; б) 1102 = 610 ; в) 10012 = 910 ; г) 1002 = 410

традиционной позиционной пятеричной системы счисления.
задание
Пятеричная система счисления

Алфавит: