Слайд 3
План работы:
Введение.Введение.
Виды систем счисления.
История развития информационных
систем.
Представление чисел, а также информации в ЭВМ.
Арифметические
операции в позиционных СС.
Применение систем счисления.
Слайд 4
«Все есть число» - так говорили древние мудрецы,
подчеркивая важнейшую роль чисел в нашей жизни.
Люди всегда пользовались
числами, считали и записывали, даже пять тысяч лет назад люди уже знали числа. Но в любом случае каждое число изображалось с помощью определенных символов – цифр.
Слайд 5
Цифры - это символы, участвующие в записи числа.
А
что же тогда число?
Число – это некоторая величина, которая
складывается из цифр по особым правилам. В разные времена и у разных народов эти правила были различны и сегодня их называют СИСТЕМАМИ СЧИСЛЕНИЯ.
Слайд 6
Система счисления – это способ записи чисел с
помощью цифр.
Системы счисления:
-позиционные
-непозиционные
Непозиционной называется такая СС, у которой вес цифры не зависит от ее местоположения в записи числа.
Непозиционные СС появились раньше позиционных и имеют долгую историю развития.
В меню
Слайд 7
История развития СС:
1) В древние времена, когда люди
начали считать, появилась потребность в записи чисел. Количество предметов
изображалось с помощью черточек или засечек на какой-либо твердой поверхности. Ученые назвали этот способ записи чисел единичной или унарной системой счисления.
Слайд 8
История развития СС:
2)Древнеегипетская десятичная СС.
Данная СС возникла
во второй половине третьего тысячелетия до н.э. Вместо цифр
использовались специальные иероглифы.
Именно из комбинации таких «цифр» записывались все числа и каждая «цифра» повторялась не более девяти раз:
Слайд 9
История развития СС:
Все числа составлялись из ключевых иероглифов
при помощи обычного сложения.
Умножение и деление производили путем последовательного
удвоения чисел.
Дроби в Египте тоже существовали и все они имели в числителе единицу (кроме числа 2/3)
Слайд 10
История развития СС:
3) Римская СС.
Данная СС не
намного отличается от египетской СС, здесь только используются совершенно
другие обозначения чисел:
I – 1 C - 100
V - 5 D - 500
X - 10 M - 1000
L - 50
Слайд 11
История развития СС:
Римская СС подразделялась также на греческую
СС. Правила этих СС были одинаковы, а обозначения различались:
Г
– пять Н - сто
Δ – десять Х - тысяча
М – десять тысяч
Слайд 12
История развития СС:
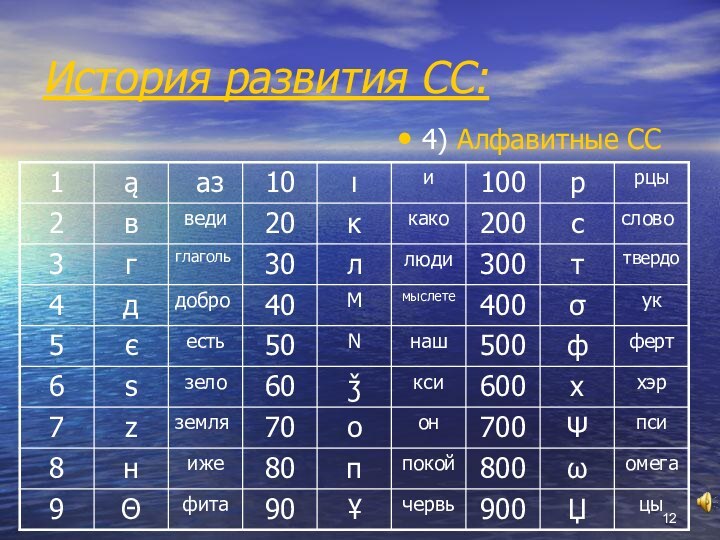
4) Алфавитные СС
Слайд 13
История развития СС:
Данная таблица – пример написания цифр
наиболее совершенной непозиционной СС, которой пользовались греки, финикийцы и
славяне. Алфавитная система была принята и в Древней Руси. До конца 17 века люди использовали 27 букв кириллицы как цифры.
Слайд 14
История развития СС:
Казалось бы, что непозиционные СС не
совсем удобны. Но наши предки умели и записывали числа
, равные 1000, 100000 и даже миллиону. Так, например, числа 1000, 2000, 3000… записывали теми же цифрами, что и 1, 2, 3… , только перед цифрой ставили слева снизу специальный знак - титла. Число 10000 обозначалось той же буквой, что и 1, только эту букву обводили кружком(это число называлось «тьма»). Число 100000 называли «легион», 10 легионов – «леорд». Самая большая из величин, имеющих свое обозначение, называлась «колода», она равнялась 1050. Считалось, что «боле сего несть человеческому уму разумевати» .
Слайд 15
История развития СС:
Так как запись чисел с помощью
алфавитной СС была достаточно сложна, то в старину на
Руси среди простого народа широко применялись СС, отдаленно напоминающие римскую. С их помощью сборщики податей заполняли квитанции об уплате подати – ясака и делали записи в податной тетради. Числа обозначали с помощью специальных символов:
- тысяча рублей
- сто рублей
- десять рублей
- 1 рубль
- 10 копеек
- копейка
Слайд 16
История развития СС:
Алфавитные СС были мало пригодны для
оперирования с большими числами. В ходе развития человеческого общества
эти системы уступили место позиционным системам.
Позиционная СС – это такая СС, в которой вес цифры (количественный эквивалент) зависит от ее местоположения в записи числа. ( Например, число 222. В его записи используется трижды цифра 2, однако вклад каждой цифры в величину числа разный. Первая 2 – это число сотен, вторая – число десятков, третья – число единиц. Эти цифры различаются и по весу. В непозиционных СС такой принцип разделения отсутствует.)
Слайд 17
История развития СС:
Позиционных СС также несколько, но наиболее
древние из них Вавилонская и Индийская мультипликативная системы.
Например, пусть
десятки обозначаются символом X, тогда сотни – Y. Число 323 будет выглядеть так: 3Y2X3. Для записи одинакового числа единиц, десяток, сотен применяются одни и те же символы, но после каждого символа пишется название соответствующего разряда. По такому принципу работают упомянутые выше СС.
Слайд 18
История развития СС:
Наиболее важным открытием является нуль. Еще
греческие астрономы использовали его для обозначения нулевого разряда (
ouden (греч) – ничто). Индийцы переняли нуль у греков и постепенно создали десятичную СС , которой мы пользуемся и по сей день. Ее в Европу завезли из Индии арабы, поэтому данная СС называется арабской.
Слайд 19
Основные свойства позиционных СС:
простота выполнения арифметических операций.
ограниченное количество
символов, необходимых для записи числа.
Примеры позиционных СС:
В меню
Слайд 20
Представление чисел в ЭВМ:
все числовые данные хранятся в
ЭВМ в двоичном виде, однако формы хранения целых и
действительных чисел различны :
целые числа хранятся в форме с фиксированной запятой.
действительные числа хранятся в форме с плавающей запятой.
Необходимость различного представления целых и действительных чисел вызвана тем, что скорость выполнения арифметических операций над числами с плавающей запятой существенно ниже скорости выполнения этих же операций над числами с фиксированной запятой.
Слайд 21
Представление текстовых данных:
Любой текст состоит из последовательности определенных
символов (букв, знаков препинания и т.д.).
Обратим особое внимание на
символ «пробел» - хотя на экране и на бумаге пробел – пустое, свободное место, на клавиатуре ЭВМ ему соответствует специальная клавиша.
Как и любая информация, текстовая информация хранится в ЭВМ в особом , закодированном (двоичном) виде.
Слайд 22
Представление текстовых данных:
Для этого каждому символу ставится в
соответствие некоторое неотрицательное число, называемое кодом символа, и это
число записывается в память ЭВМ в двоичном виде. Конкретное соответствие между символами и их кодами называется системой кодировки. В современных ЭВМ, как правило, используются 8-разрядные коды символов (реже – 16-разрядные).Использование данных кодов позволяет закодировать 256 различных символов, что вполне достаточно для практических нужд. При этом код символа занимает ровно 1 байт памяти.
Слайд 23
Представление графической информации в ЭВМ:
Мониторы современных ПК могут
работать в двух режимах: текстовом и графическом.
В текстовом режиме
экран разбивается на 25 строк по 80 символов в строке. Данный режим предназначен для вывода на экран монитора текстов и простых рисунков.
В графическом режиме экран разделяется на отдельные светящиеся точки – пиксели. Любое графическое изображение хранится в памяти в виде информации о каждом пикселе на экране. Состояние каждого пикселя описывается последовательностью нулей и единиц, соответствующих кодировке его цвета. Такую форму представления изображений называют растровой.
Слайд 24
Представление звуковой информации:
Развитие ЭВМ в последнее время позволяет
записывать и воспроизводить на компьютерах музыку и человеческую речь.
Существует 2 способа звукозаписи:
цифровая запись – реальные звуковые волны, которые преобразуются в цифровую информацию путем измерения звука тысячи раз в секунду. Этот процесс называется дискретизацией и возможен на компьютере, если на нем присутствует звуковая плата. Форматы звука: mp3, WAV и т.д.
MIDI-запись – это не реальный звук, а запись определенных команд-указаний. MIDI-запись – электронный эквивалент нотной записи.
Существуют также видео файлы – это сложный синтез звуковой дорожки и графических изображений.
В меню
Слайд 25
Арифметические операции в позиционных СС:
Итак, мы выяснили, что
в ЭВМ любая информация (графическая, текстовая и т.д.) кодируется
и записывается с помощью всего двух цифр – нуля и единицы (двоичное кодирование). И над этими цифрами можно провести арифметические операции, такие как сложение и вычитание, умножение и деление. Рассмотрим это более подробно:
Слайд 26
Арифметические операции в позиционных СС:
1) Перевод чисел из
P-ичной СС в десятичную.
Допустим, дано число в P-ичной СС.
Требуется получить его запись в десятичной СС. Для этого представим данное число в развернутой форме a=a(n)*P(n)+a(n-1)*P(n-1)+…+a(1)*P+a(0) и воспользуемся алгоритмом решения данной задачи:
Слайд 27
Арифметические операции в позиционных СС:
- каждая цифра числа
в P-ичной СС переводится в число в десятичной СС.
-
полученные числа нумеруются справа налево начиная с нуля (номера соответствуют степеням P в многочлене)
- десятичное число, соответствующее каждой P-ичной цифре, умножается на P(k), где k-номер этого числа из пункта 2,и результаты складываются, причем все эти арифметические действия проводятся в десятичной СС.
Слайд 28
Арифметические операции в позиционных СС:
Примеры перевода чисел:
1) Переведем
1001101(2) – двоичное число в A(10): 1001101(2)=2^0+2^2+2^3+2^6=77(10)
2) Переведем 2143(5)
в A(10): 2143(5)=2*5^3+1*5^2+4*5+3=298(10)
Задания: 1) Перевести из B0F9(16) в А(10). 2) Перевести из 1101(2) в А(10).
Слайд 29
Арифметические операции в позиционных СС:
2) Сложение и вычитание.
Во
всех традиционных СС эти арифметические операции выполняются по одним
и тем же правилам (согласно специальным таблицам). В P-ичной СС таблица сложения – это результат сложения каждой цифры алфавита P-ичной СС с любой другой цифрой этой же СС. Достаточно простой таблицей является таблица сложения в двоичной СС:
В шестнадцатеричной СС такая таблица во много раз массивней и больше.
Слайд 30
Арифметические операции в позиционных СС:
Примеры сложения чисел:
101,01(2) 21(3) – троичная СС
+
1,11(2) + 2,1(3)
------------- --------
111,00(2) 100,1(3)
Задания: Сложите : 11010101(2) и 1110(2); 1234(5) и 4321(5).
Слайд 31
Арифметические операции в позиционных СС:
Вычитание из большего числа
меньшего в P-ичной СС тоже производится столбиком аналогично вычитанию
в десятичной СС с использованием все той же таблицы сложения в P-ичной СС.
Примеры вычитания:
101(2) 210(3)
- 10,1(2) - 102(3)
------------ -----------
10,1(2) 101(3)
Задания: 4321(5) - 1234(5); 11010101(2) - 1110(2).
Слайд 32
Арифметические операции в позиционных СС:
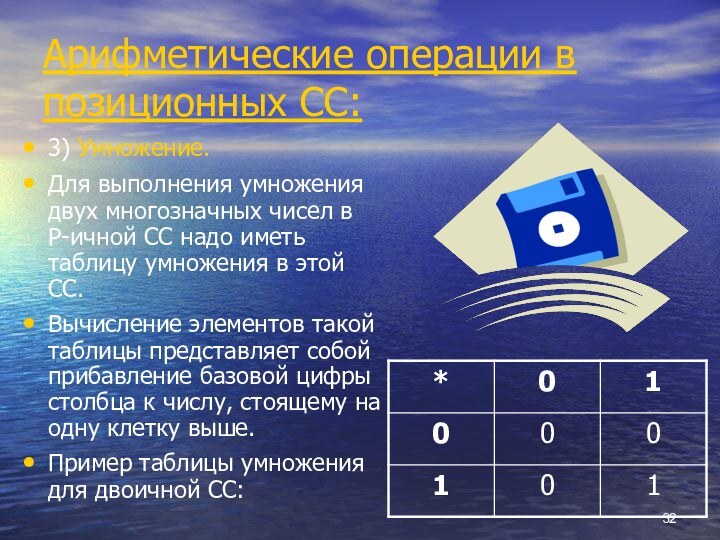
3) Умножение.
Для выполнения умножения
двух многозначных чисел в P-ичной СС надо иметь таблицу
умножения в этой СС.
Вычисление элементов такой таблицы представляет собой прибавление базовой цифры столбца к числу, стоящему на одну клетку выше.
Пример таблицы умножения для двоичной СС:
Слайд 33
Арифметические операции в позиционных СС:
Пример умножения чисел:
10100(2)
* 1010(2)
Задания:
--------------- 1)1101(2)*1110(2)
101 2)4321(5)*123(5)
+ 101
----------------
11001000(2)
Слайд 34
Арифметические операции в позиционных СС:
4) Деление.
При делении столбиком
в P-ичной СС приходится в качестве промежуточных вычислений выполнять
действия умножения и вычитания, а следовательно , используются таблицы умножения и сложения в данной P-ичной СС.
Пример деления чисел:
11110(2) | 110(2)
- 110(2) | 101(2) Задания:
--------------- 1)10010000(2):1110(2)
110 2)4322(5):3(5)
- 110
----------------
0
В меню
Слайд 35
Применение систем счисления:
В настоящее время СС используются в
основном в компьютерной технике и в информационных технологиях, однако
некоторые СС применяются в других науках (математике например) или даже в повседневной жизни (например, в Китае в настоящее время используют пятеричную СС). Поэтому можно сказать , что СС востребованы и широко используются.
В меню