при этом каждая переменная встречается не более одного раза
(либо сама, либо ее инверсия)Пример x^y^¬z
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть











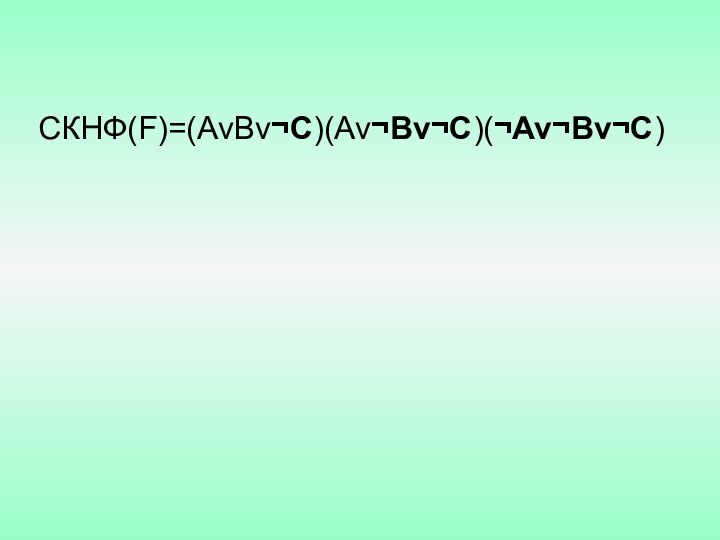


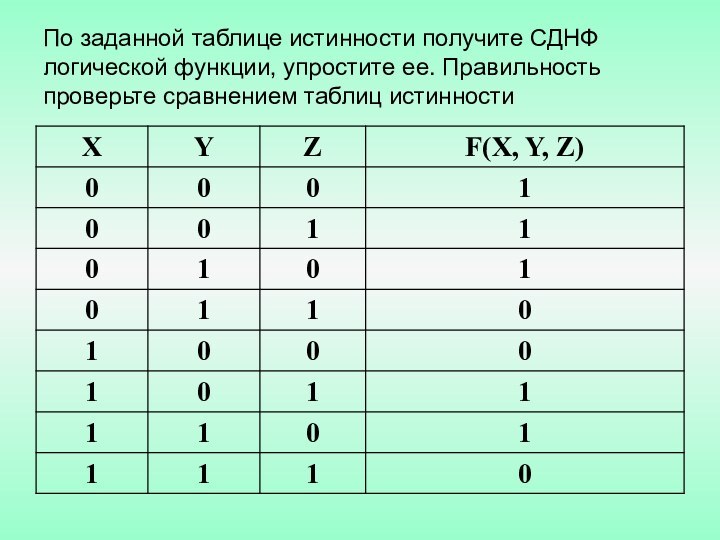

Пример x^y^¬z
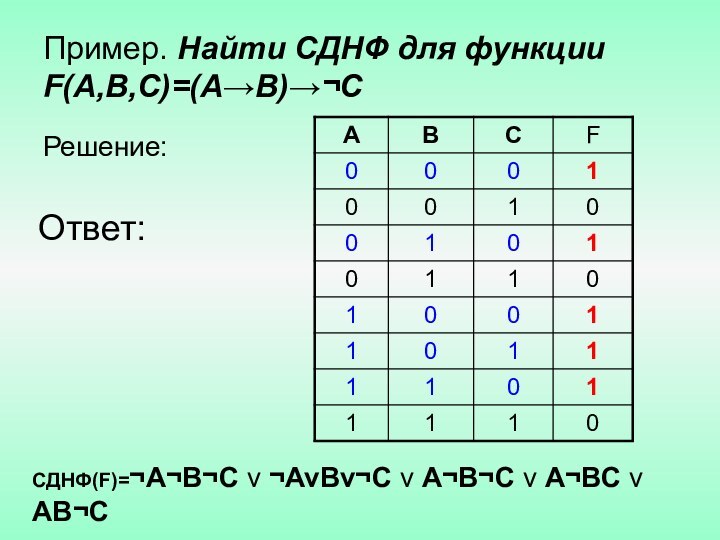
Пример: f (A, B, C)=ABC v A¬(BC) v ¬AB¬C
Пример. Xv¬YvZ
Пример. f(A,B,C)=(AvBvC)(¬AvBvC)(Av¬Bv¬C)
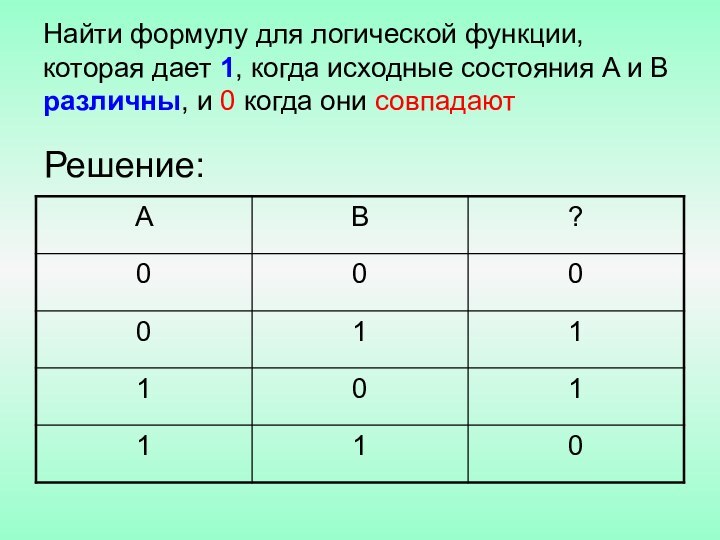
Решение: