- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Векторная компьютерная графика
Содержание
- 2. Мир компьютерной графикиГреческие философы-пифагорейцы утверждали, что весь
- 3. Миром правят
- 4. Пример растровой графики
- 5. Фрактальная графикаВ математике существует понятие фрактала –
- 6. Примеры фрактальной графики.
- 7. Фракталы в природе Многие природные объекты самоподобны
- 8. Пример векторной графики
- 9. Векторная графикаВ основе векторной графики лежат математические
- 10. Кривая БезьеПрограмма CorelDraw является редактором изображений, состоящих
- 11. Продукция компании RENO
- 12. Начало-началСобственно математическая теория, на основе которой появилась
- 13. Уравнение 3-го порядка.В качестве формулы, которая была
- 14. Вид кривой БезьеОбщий вид элементарной кривой Безье
- 15. Узлы кривой Безье.Из четырех контрольных точек кривая
- 16. Управление объектом с помощью «рычагов» кривизны Две
- 17. Кривая Безье является гладкой кривой, т. е.
- 18. Масштабирование кривой Безье.Кривая Безье, используя математический язык,
- 19. Скачать презентацию
- 20. Похожие презентации
Мир компьютерной графикиГреческие философы-пифагорейцы утверждали, что весь мир — число. И если в отношении всего мира, возможно, философы и преувеличили значение числа, то в отношении компьютерных технологий они оказались безусловно правы: весь компьютерный мир — число.


















Слайд 3 Миром правят числа
Мечтатели, сабиллы и пророки
Дорогами, запретными для мысли,
Проникли -вне сознания
-далеко,Туда, где светят царственные числа.
Валерий Брюсов «Числа»
Слайд 5
Фрактальная графика
В математике существует понятие фрактала – геометрического
образования, представляющего собой систему самоподобных фигур, расположенных относительно друг
друга закономерным образом. Как форма и размер отдельных элементов, так и их взаимное расположение может быть описано математической формулой
Слайд 7
Фракталы в природе
Многие природные объекты самоподобны и
состоят из повторяющихся элементов разных размеров. Очевидные примеры –
дерево, куст, колония кораллов. Еще более наглядным примером может служить соцветие «сложный зонтик» – «зонтик», состоящий, в свою очередь, из маленьких зонтиков.
Слайд 9
Векторная графика
В основе векторной графики лежат математические представления
о свойствах математических фигур.
Простейшим объектом векторной графики является линия.
Слайд 10
Кривая Безье
Программа CorelDraw является редактором изображений, состоящих из
объектов — векторных контуров, которым после их создания могут
присваиваться параметры обводок и параметры заливок. Контуры, в свою очередь, описываются математическими формулами, в частности используется так называемая кривая Безье, названная в честь французского математика Пьера Безье (P. Bezier), который применял математические кривые и поверхности в процессе конструирования кузова автомобиля "Рено".
Слайд 12
Начало-начал
Собственно математическая теория, на основе которой появилась возможность
использовать кривые в различных прикладных областях, была сформулирована в
начале века российским и советским математиком академиком Сергеем Натановичем Бернштейном (1880—1968), который в 1899 году окончил Парижский университет.
Слайд 13
Уравнение 3-го порядка.
В качестве формулы, которая была бы
достаточно простой (с точки зрения математика), универсальной (с точки
зрения программиста) и геометрически наглядной (с точки зрения пользователя — художника или дизайнера), чаще всего используется упомянутая кривая Безье. На самом деле, это целое семейство кривых, из которых используется частный случай с кубической степенью, т. е. кривая третьего порядка, описываемая следующим параметрическим уравнением:где 0_< t _<1
Слайд 14
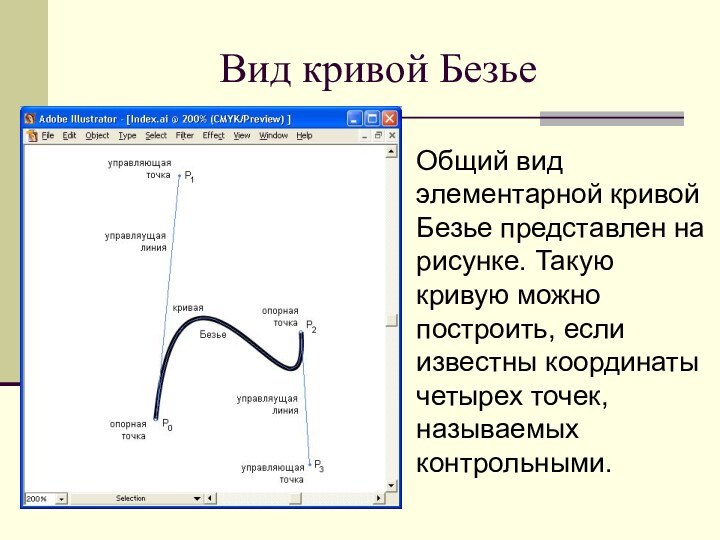
Вид кривой Безье
Общий вид элементарной кривой Безье представлен
на рисунке. Такую кривую можно построить, если известны координаты
четырех точек, называемых контрольными.
Слайд 15
Узлы кривой Безье.
Из четырех контрольных точек кривая проходит
только через две, поэтому эти точки называются опорными —
anchor points (иначе они именуются узлами (nodes), поскольку "связывают" элементарные кривые друг с другом, чтобы образовать единый сложный контур).
Слайд 16
Управление объектом с помощью «рычагов» кривизны
Две контрольные
точки не лежат на кривой, но их расположение определяет
кривизну кривой, поэтому эти точки иначе называются управляющими точками, а линии, соединяющие управляющую и опорную точки, — управляющими линиями (в просторечии именуются "рычагами").Слайд 17 Кривая Безье является гладкой кривой, т. е. она
не имеет разрывов и непрерывно заполняет отрезок между начальной
и конечной точками.Кривая начинается в первой опорной точке, касаясь отрезка своей управляющей линии, и заканчивается в последней опорной точке, также касаясь отрезка своей управляющей линии. Это позволяет гладко соединять две кривые Безье друг с другом: управляющие линии располагаются вдоль одной прямой, которая является касательной к получившейся кривой.