- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему англия в раннее средневековье
Содержание
- 2. Австрии ИндонезииМатематический диктант "Флаги" Тема: «Обыкновенные дроби»Каждый флаг разделен на несколько равных частей. Ответьте на вопросы:
- 3. красным – не закрашена – зелёным –Проверьте
- 4. Задача: Разделим 5 яблок между тремя детьми
- 5. 2 способ.Можно дать каждому ребёнку по яблоку,
- 6. В числе число 1
- 7. Чтобы из неправильной дроби выделить целую часть,
- 8. Пример:Выделить целую часть из неправильной дроби
- 9. Число, состоящее из целой части и дробной части, называют смешанным числом.Задание. Прочитайте смешанные числа:
- 10. Смешанное число можно представить в виде неправильной
- 11. Чтобы представить смешанное число в виде неправильной
- 12. В классе: № 1057,
- 13. Скачать презентацию
- 14. Похожие презентации
Австрии ИндонезииМатематический диктант "Флаги" Тема: «Обыкновенные дроби»Каждый флаг разделен на несколько равных частей. Ответьте на вопросы:











Слайд 2
Австрии
Индонезии
Математический диктант "Флаги"
Тема: «Обыкновенные дроби»
Каждый флаг
разделен на несколько равных частей. Ответьте на вопросы:
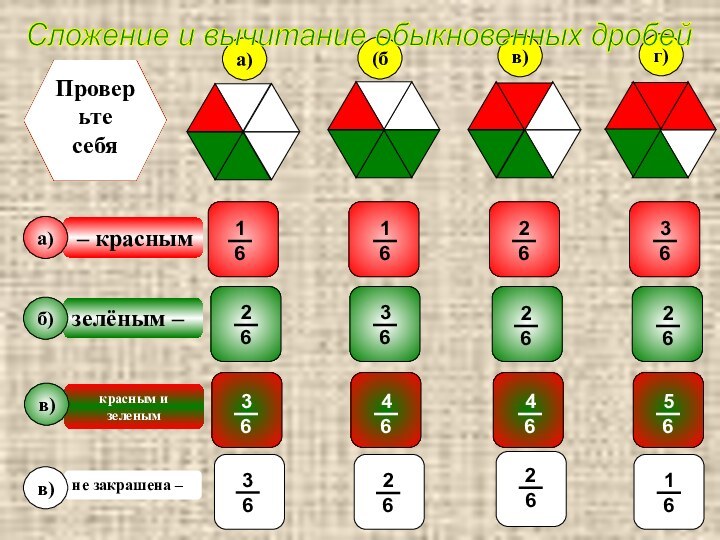
Слайд 3
красным –
не закрашена –
зелёным –
Проверьте
себя
a)
б)
в)
a)
б)
в)
г)
красным
и зеленым
в)
Проверьте
себя
Проверьте
себя
Проверьте
себя
Сложение и вычитание обыкновенных дробей
Слайд 4
Задача: Разделим 5 яблок между тремя детьми
поровну. 1 способ
Разделим каждое яблоко на
три равные части, тогда каждый ребёнок получит по 5 частей, а каждая из этих частей равна целого яблока. Значит каждый ребёнок получит яблока.
Слайд 5
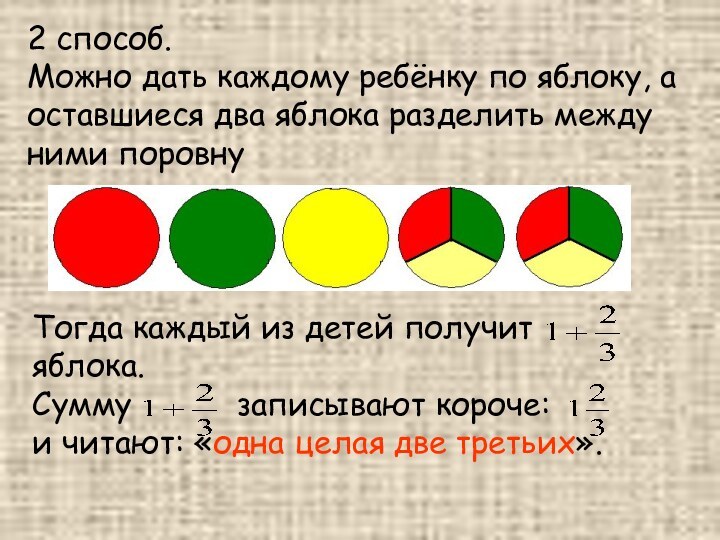
2 способ.
Можно дать каждому ребёнку по яблоку, а
оставшиеся два яблока разделить между ними поровну
Тогда каждый из
детей получит яблока.
Сумму записывают короче:
и читают: «одна целая две третьих».
Слайд 6 В числе число 1 называют
целой частью, а число - его дробной
частью.Так как в обоих случаях каждый ребёнок получает одно и то же количество яблок, то числа и
равны, т.е. = .
Чтобы из получить , надо разделить 5 на 3. Получим неполное частное 1 и остаток 2. Число 1 даёт целую часть, а остаток 2 – числитель дробной части.
Слайд 7
Чтобы из неправильной дроби выделить целую часть, надо:
разделить с остатком числитель на знаменатель;
2) неполное частное будет
целой частью;3) остаток (если он есть) даёт числитель, а делитель – знаменатель дробной части.
Слайд 8
Пример:
Выделить целую часть из неправильной
дроби
.
Делим 42 на 5.
_42 5
40 82
Неполное частное равно 8, а остаток 2.
Значит, .
Слайд 9 Число, состоящее из целой части и дробной части,
называют смешанным числом.
Задание. Прочитайте смешанные числа:
Слайд 10
Смешанное число можно представить в виде неправильной дроби.
Пример:
Представим в виде неправильной дроби число
.
Слайд 11
Чтобы представить смешанное число в виде неправильной дроби,
нужно:
умножить его целую часть на знаменатель дробной части;
к полученному
произведению прибавить числитель дробной части;3) записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.





























