- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Уроки истории математики как одна из форм использования исторического материала в процессе обучения
Содержание
- 2. Здравствуйте, ребята!Я – профессор Задачкин – специалист
- 3. В путешествии нам потребуется универсальный «переводчик»!АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
- 4. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИС ПОМОЩЬЮ УРАВНЕНИЯ:1. Внимательно прочитайте
- 5. Наш путь лежит в Древний Египет!
- 6. Больше, чем
- 7. Самый
- 8. В папирусе Ахмеса содержатся
- 9. Задача 1. «Количество и ее четвёртая часть
- 10. Задача 2. «Найти число, если известно, что
- 11. Задача 3. Некий математик
- 12. Нас ждётДревняя Греция !
- 13. Настоящей наукой математика стала
- 14. Много греческих математиков
- 15. Задача 4. «Жизнь Диофанта»Прах Диофанта гробница покоит
- 17. Задача 5. «Школа Пифагора»
- 18. Задача 6. «О статуе Минервы»Я – изваянье
- 19. Вперёд!В Древнюю Индию!
- 20. В Индии математика зародилась примерно
- 21. Задача 7. «Индийская задача Сриддхары »Есть кадамба
- 22. Решение:Ответ: 15 пчёл.
- 23. А теперь путь наш лежит вЕвропу!
- 24. В Европе центрами распростра-нения знаний
- 25. «Чтобы решить вопрос, относящийся к числам или
- 26. Задача 8. «Французская задача» Когда у
- 27. Задача 9. «Задача Этьенна Безу»
- 28. Задача 10. «Чешская задача» По преданию,
- 29. Задача 11. «Немецкая задача» Сын
- 30. ДОМОЙ !!!В Россию !
- 31. «Нет ни
- 32. На Руси особенно важную
- 33. Задача 12. "Некий человек нанял работника
- 34. Задача 13. Торговка продавала цыплят. Одна
- 35. Задача 14. На вопрос о том,
- 36. Задача 15. Летела стая гусей, навстречу
- 37. Наше путешествие подошло к концу.Спасибо за внимание!До новых встреч, друзья!
- 38. Скачать презентацию
- 39. Похожие презентации
Здравствуйте, ребята!Я – профессор Задачкин – специалист по древним математическим рукописям.Предлагаю вам совершить увлекательное путешествие в мир старинных задач!



































Слайд 2
Здравствуйте, ребята!
Я – профессор Задачкин – специалист по
древним математическим рукописям.
старинных задач!
Слайд 4
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
С ПОМОЩЬЮ УРАВНЕНИЯ:
1. Внимательно прочитайте за-дачу.
2.
Разбейте условие задачи на отдельные ситуации.
3. Обозначьте неизвестное чи-сло
буквой х (обычно искомую величину).4. Выразите другие неизвест-ные через х.
5. Используя условие задачи, составьте уравнение.
6. Решите уравнение.
7. Запишите ответ к задаче.
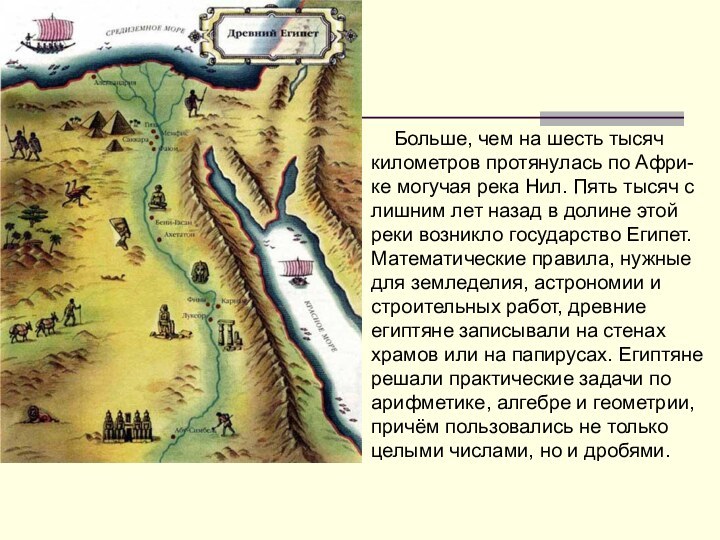
Слайд 6 Больше, чем на
шесть тысяч километров протянулась по Афри-ке могучая река Нил.
Пять тысяч с лишним лет назад в долине этой реки возникло государство Египет. Математические правила, нужные для земледелия, астрономии и строительных работ, древние египтяне записывали на стенах храмов или на папирусах. Египтяне решали практические задачи по арифметике, алгебре и геометрии, причём пользовались не только целыми числами, но и дробями.Слайд 7 Самый большой,
сохранившийся до наших дней, древнеегипетский математический текст – это
так называемый папирус писца Ахмеса (18 – 17 вв.до н.э.).Папирус содержит 84 задачи.
Папирус был приобретён в 1858 году Г. Райндом и изучен впервые профессором А. Эйзенлором в 1877 году.
Слайд 8
В папирусе Ахмеса
содержатся
задачи, в которых неизвестное имеет особый символ и название:
«хау» или «аха».
Оно означает:
«количество», «куча».
Так называемое
«исчисление кучи»,
или
«вычисление хау», приблизительно соответствует нашему решению задач
с помощью уравнений.
Слайд 9
Задача 1.
«Количество и ее четвёртая часть дают
вместе 15».
Ответ: для решения задачи составляется уравнение
х + ¼ х = 15х = 12.
Слайд 10
Задача 2.
«Найти число, если известно, что от
прибавления
к нему 2/3 его и вычитания от
полученной суммы её трети, получается 10». Ответ: 9.
Слайд 11
Задача 3.
Некий математик насчитал
на выгоне 70 коров.
«Какую долю
от всего стада составляют эти коровы?» - спросил математик у пастуха. «Я выгнал пастись две трети от трети всего стада», - ответил пастух. Сколько голов скота насчитывается во всём стаде?
Слайд 13 Настоящей наукой математика стала только
у древних греков. Греки не просто заучивали пра-вила, а
доискивались причины. Каждое правило греческие ма-тематики старались объяснить и доказать, что оно действи-тельно верное. Для этого они спорили друг с другом, рассу-ждали, старались найти в рас-суждениях ошибки. Из правил складывались законы, из зако-нов – наука математика.Слайд 14 Много греческих математиков внесли
свой вклад в разви-тие науки, одним из них был
Диофант. Диофант большое внимание в своих работах уделял уравнениям.«Посредством уравнений, теорем
Он уйму всяких разрешил проблем:
И засухи предсказывал, и ливни –
Поистине его познанья дивны!»
Слайд 15
Задача 4. «Жизнь Диофанта»
Прах Диофанта гробница покоит дивись
ей - и камень.
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком,
И половину шестой встретил с пушком на щеках.
Только минула седьмая, подружкою он обручился.
С ней пять лет проведя, сына дождался мудрец.
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе.
Тут и увидел предел жизни печальной своей.
Слайд 17
Задача 5. «Школа Пифагора»
Говорят, что на вопрос, сколько у него учеников, древнегре-ческий
математик Пифагор ответил так:"Половина моих учеников изучает математику, четвертая часть изучает природу, седьмая часть проводит время в мол-чаливом размышлении. Остальную часть составляют три девы".
Сколько учеников было у Пифагора?
Слайд 18
Задача 6. «О статуе Минервы»
Я – изваянье из
злата.
Поэты то злато в дар принесли:
Харизий принёс
половину всей жертвы,Феспия часть восьмую дала; десятую Солон.
Часть двадцатая – жертва певца Фемисона, а девять
Всё завершивших талантов – обет,
Аристоником данный.
Сколько же злата поэты все вместе в дар принесли?
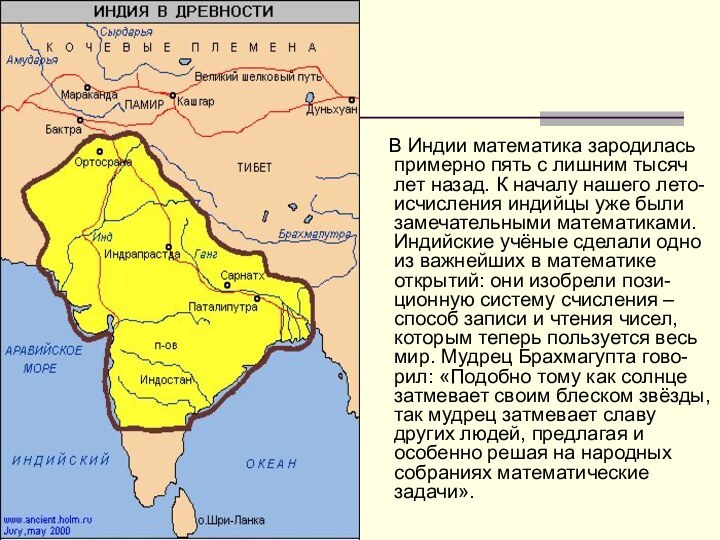
Слайд 20 В Индии математика зародилась примерно пять
с лишним тысяч лет назад. К началу нашего лето-исчисления
индийцы уже были замечательными математиками. Индийские учёные сделали одно из важнейших в математике открытий: они изобрели пози-ционную систему счисления – способ записи и чтения чисел, которым теперь пользуется весь мир. Мудрец Брахмагупта гово-рил: «Подобно тому как солнце затмевает своим блеском звёзды, так мудрец затмевает славу других людей, предлагая и особенно решая на народных собраниях математические задачи».
Слайд 21
Задача 7. «Индийская задача Сриддхары »
Есть кадамба цветок.
На один лепесток
Пчёлок пятая часть опустилась.
Рядом тут же росла
вся в цвету сименгда,И на ней третья часть поместилась.
Разность их ты найди, трижды их ты сложи,
на кутай этих пчёл посади.
Лишь одна не нашла себе места нигде,
всё летала то взад, то вперёд.
И везде ароматом цветов наслаждалась.
Назови теперь мне, подсчитавши в уме,
сколько пчёлок всего здесь собралось?
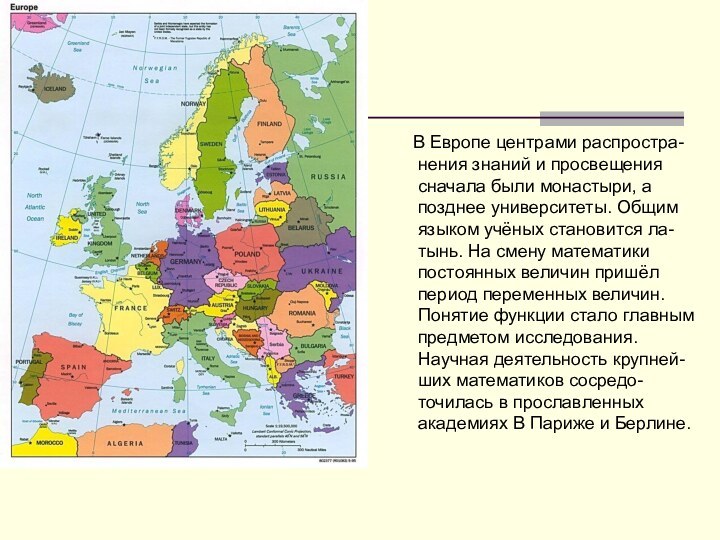
Слайд 24 В Европе центрами распростра-нения знаний и
просвещения сначала были монастыри, а позднее университеты. Общим языком
учёных становится ла-тынь. На смену математики постоянных величин пришёл период переменных величин. Понятие функции стало главным предметом исследования. Научная деятельность крупней-ших математиков сосредо-точилась в прославленных академиях В Париже и Берлине.
Слайд 25
«Чтобы решить вопрос, относящийся к числам или отвлечённым
отношениям величин, нужно лишь перевести задачу с родного языка
на язык алгебраический»И. Ньютон
«Всеобщая арифметика»
Слайд 26
Задача 8. «Французская задача»
Когда у старушки
Леони спрашивают, сколько у неё кошек, она меланхолично отвечает:
«Четыре пятых моих кошек плюс четыре пятых кошки». Сколько же у Леони кошек?
Слайд 27
Задача 9. «Задача Этьенна Безу»
По
контракту работникам при-читается по 48 франков за каж-дый отработанный
день, а за каждый неотработанный день с них взыскивается по 12 фран-ков. Через 30 дней выяснилось, что работникам ничего не при-читается. Сколько дней они отработали в течение этих 30 дней?Решение: 48х – 12(30 – х) = 0,
х = 6.
Слайд 28
Задача 10. «Чешская задача»
По преданию, основательница
чешского государства принцесса Либуша обещала отдать свою руку тому
из трёх женихов, кто сумеет решить задачу: «Если бы я дала первому жениху половину слив из этой корзины и ещё одну сливу, второму жениху половину оставшихся слив и ещё одну сливу, а оставшиеся сливы подели-ла пополам и половину их и ещё три сли-вы отдала бы третьему жениху, то корзи-на опустела бы. Сколько слив в корзи-не?»
Слайд 29
Задача 11. «Немецкая задача»
Сын спросил
отца, сколько ему лет.
Отец ответил
так: «Если прибавить к моим годам их половину, затем их четверть и ещё один год, то получится 134 года» Сколько лет отцу?
Слайд 31
«Нет ни одной
страны, кото-рая не поддерживала бы с математикой дружеских отно-шений,
не приумножала её сокровищ и славы». Русские математики внесли огромный вклад в математическую науку.А.И. Маркушевич
Слайд 32 На Руси особенно важную роль
сыграла книга «Ариф-метика или наука числитель-ная», написанная Магницким Леонтием
Филипповичем, которая была издана при Петре Первом в 1703 году. Она долгое время была настольной книгой всех обра-зованных русских людей. Это была настоящая энциклопе-дия по математике, в кото-рой каждое правило, каждый приём подробно разъяснялся и подкреплялся решением примеров и практических задач.
Слайд 33
Задача 12.
"Некий человек нанял работника на
год, обещал ему дать 12 руб. и кафтан. Но
тот, отработав 7 меся-цев, захотел уйти и просил достойной платы с кафта-ном. Хозяин дал ему по достоинству расчет 5 р. и кафтан. Спрашивается, а какой цены тот кафтан был?"7 · (x + 12):12 = x + 5,
где x руб. — стоимость кафтана.
Кафтан стоил 4 руб. 80 коп.
Слайд 34
Задача 13.
Торговка продавала цыплят. Одна кухарка
купила у неё полови-ну всех цыплят и ещё полцыплёнка.
Другая кухарка купила поло-вину всех оставшихся цыплят и ещё полцыплёнка. Наконец, третья кухарка купила половину всех оставшихся цыплят и ещё полцыплёнка, после чего у торговки не осталось ни одного цы-плёнка. Сколько у неё было цыплят, если все купленные кухар-ками цыплята были живыми?
Слайд 35
Задача 14.
На вопрос о том, сколько
времени, был дан такой ответ: «Две пятых времени, прошедшего
от полуночи до этого момента, равно двум третьим времени, которое осталось до полудня». Сколько сейчас времени?