Слайд 2
История «Золотого сечения»
История “Золотого сечения” - это история
человеческого познания мира. Понятие “Золотое сечение” прошло в своем
развитии все стадии познания. Первая ступень познания - открытие “золотого сечения” древними пифагорейцами. От простого созерцания действительности они перешли к выражению его в мире чисел, но ими были спутаны причинно-следственные понятия мира и догадка о мировой значимости “Золотого сечения” осталась лишь догадкой на века. И все же, в своей жизнедеятельности человек начинает использовать “Золотое сечение” в своих художественных произведениях.
Вся древнегреческая культура развивалась под знаком золотой пропорции. Греки первые установили: пропорции хорошо сложенного человеческого тела подчиняются ее законам, что особенно хорошо видно на примере античных статуй. В наши дни интерес к золотой пропорции возрос с новой силой. В целом ряде музыковедческих работ подчеркивается наличие золотого сечения в композиции произведений Баха, Шопена, Бетховена.
Слайд 3
В эпоху Ренессанса золотая пропорция возводится в

ранг главного эстетического принципа. Леонардо да Винчи, Рафаэль, Микеланджело,
Тициан и другие великие художники возрождения компонуют свои полотна, сознательно используя золотую пропорцию. Нидерландский композитор XV века Якоб Обрехт широко использует “Золотое сечение” в своих музыкальных композициях, которые до сих пор уподобляют “кафедральному собору”, созданному гениальным архитектором.
Практические нужды торговли подводят Фибоначчи к открытию своих рядов, которые еще никто не связывает с “Золотым сечением”. В XIX веке уже не художники, а ученые-экспериментаторы, изучавшие закономерности филлотаксиса (расположение цветков), вновь обратились к золотой пропорции. Оказалось, что цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках и т. д. “упакованы” по логарифмическим спиралям, завивающимся навстречу друг другу. При этом числа “правых” и “левых” спиралей всегда относятся друг к другу, как соседние числа Фибоначчи (13:8, 21:13, 34:21, 55:34), предел последовательности которых является золотая пропорция
Слайд 6
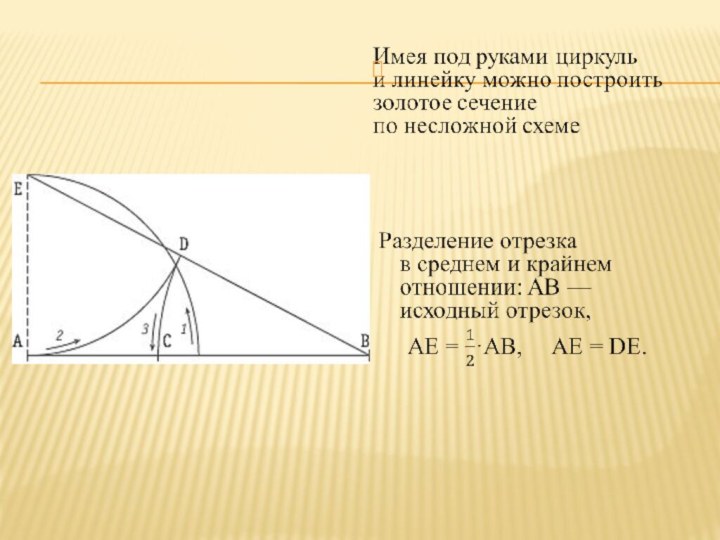
Золотое сечение можно вычислить еще проще, без геометрии
и без алгебры, — для этого используют приближенные значения 0,62 и 0,38.
Если целый отрезок принять за 100 частей, то большая часть отрезка равна 62, а меньшая — 38 частям.
Слайд 7
Ряд Фибоначчи
С историей золотого сечения косвенным образом связано
имя итальянского математика монаха - Леонардо из Пизы, более
известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится?». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:
Месяцы: 0 1 2 3 4 5 6 7 8 9 10 11 12 и т.д.
Пары кроликов: 0 1 1 2 3 5 8 13 21 34 55 89 144 и т.д.
Слайд 8
Ряд чисел 0, 1, 1, 2, 3, 5,

8, 13, 21, 34, 55 и т.д. известен как
ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как к арифметическому выражению закона золотого деления.
Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга, и зрительного восприятия.
Слайд 9
Филлотаксис
Все в Природе подчинено строгим математическим законам. Оказывается,

что расположение листьев на стеблях также носит строгий математический
характер и это явление называется в ботанике "филлотаксисом". Суть филлотаксиса состоит в винтовом расположении листьев на стебле растений (ветвей на деревьях, лепестков в соцветьях и т.д.).
В явлении филлотаксиса используются более сложные понятия симметрии, в частности понятие "винтовая ось симметрии". Рассмотрим, например, расположение листьев на стебле растения. Мы видим, что листья находятся на различных высотах стебля вдоль винтовой линии, обвивающейся вокруг его поверхности. Для того чтобы перейти от нижележащего листа к следующему, приходится мысленно повернуть лист на некоторый угол вокруг вертикальной оси стебля, а затем поднять его на определенный отрезок вверх. В этом и состоит суть "винтовой симметрии".
Ботаники утверждают, что дроби, характеризующие винтовые оси растений, образуют строгую математическую последовательность, состоящую из отношений соседних чисел Фибоначчи, то есть:
1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34, ... .(1)Вспомним, что ряд Фибоначчи есть следующая последовательность чисел:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... . (2)