- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Производная функции
Содержание
- 2. История возникновения понятия производнойЗадачи, приводящие к понятию производнойОпределение производной функцииПрактическое применение производнойСодержание
- 3. ИСАА́К НЬЮ́ТОН 1642 —1727английский физик, математик,
- 4. ∆t t Пусть вдоль некоторой прямой движется точка по
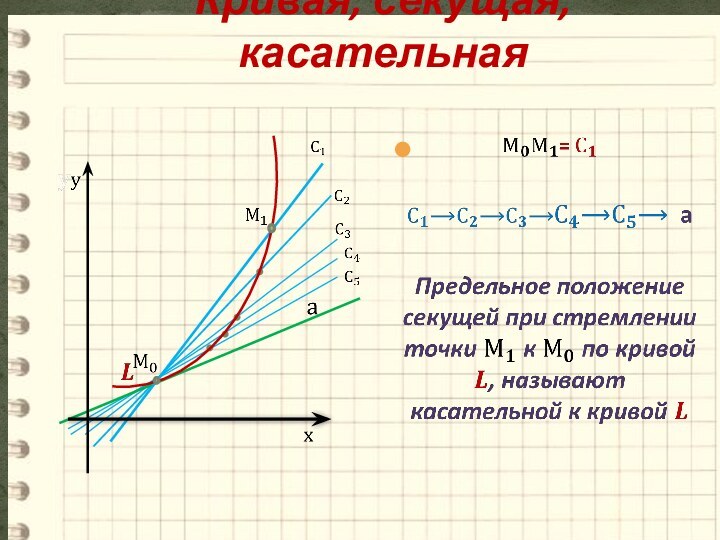
- 5. Кривая, секущая, касательная
- 6. Тангенс углаТангенс угла в прямоугольном треугольникеУгловой коэффициент
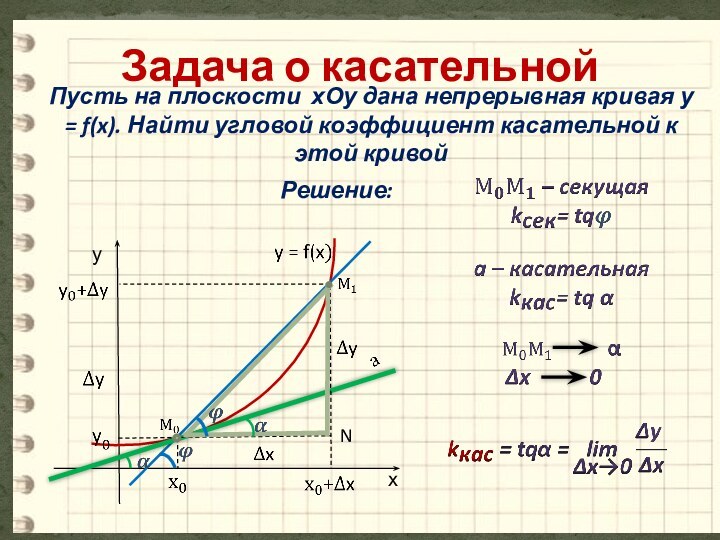
- 7. Пусть на плоскости хОу дана непрерывная кривая
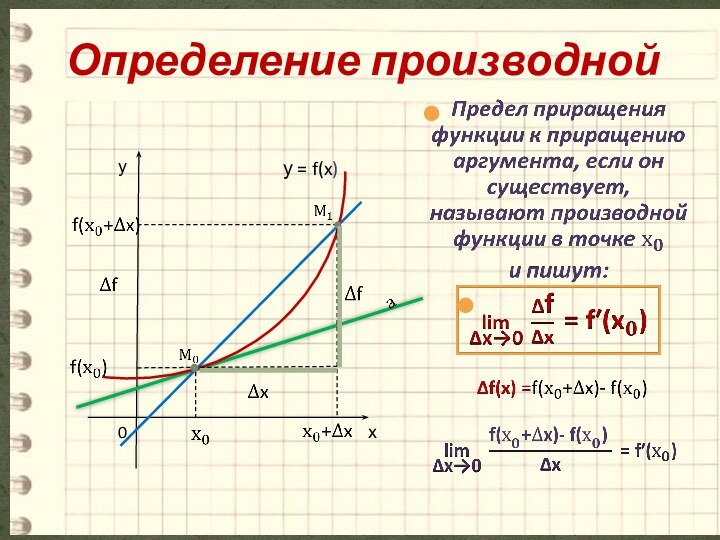
- 8. Определение производной ух0 у = f(x)
- 9. Выводы
- 10. Скачать презентацию
- 11. Похожие презентации
История возникновения понятия производнойЗадачи, приводящие к понятию производнойОпределение производной функцииПрактическое применение производнойСодержание







Слайд 2
История возникновения понятия производной
Задачи, приводящие к понятию производной
Определение
производной функции
Слайд 3
ИСАА́К НЬЮ́ТОН
1642 —1727
английский физик, математик, механик и
астроном
Великие ученые XVII века
ГО́ТФРИД ВИ́ЛЬГЕЛЬМ ЛЕ́ЙБНИЦ
1646 —1716
немецкий философ,
логик, математик, механик, физик, юрист, историк, дипломат, изобретатель и языковед
Слайд 4
∆t
t
Пусть вдоль некоторой прямой движется точка по закону
S=S(t), где S – пройденный путь; t – время.
Необходимо найти скорость точки в момент времени t0.
Задача о скорости движения
Слайд 6
Тангенс угла
Тангенс угла в прямоугольном треугольнике
Угловой коэффициент линейной
функции
y = kx+b - линейная функция.
k - угловой коэффициент
прямой.Угол α – углом между этой прямой и положительным направлением оси Ox.
a
y = kx+b
α
α
x
y
0
k =tq α
c
Слайд 7 Пусть на плоскости хОу дана непрерывная кривая у
= f(x). Найти угловой коэффициент касательной к этой кривой
Решение:
Задача
о касательной
N
у
х