- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Межпредметные связи на уроках геометрии как средство развития познавательной деятельности учащихся
Содержание
- 2. Объект математики - весь мир, и его
- 4. Цели урока:1. Образовательная: познакомить и научить учащихся
- 5. Учитель геометрии. Построением правильных фигур мы уже
- 6. 11 класс. Тема «Конус».Вопрос: «Какая связь между этой картиной и темой урока?»
- 7. Триангуляция (от лат. triangulum — треугольник) - это способ измерения площадей на местностиИзмерение расстояния до недосягаемой точки
- 8. Урок обобщения, повторения и коррекции знаний по теме «Векторы»
- 9. Примеры задач на применение векторных величинТест с
- 10. Задача 1. Силы, действующие на брусок, расположенный на
- 11. Задание «Эксперементальное»На узелок действуют три силы,
- 12. 1. В бассейне с горизонтальным дном площадью
- 13. ЕГИПЕТСКАЯ ПИРАМИДА Если сложить четыре стороны
- 14. МЕДИАНА ТРЕУГОЛЬНИКАЦентр массмАВСА1С1В1ЦентроидЗагадкаНас трое в треугольнике любом.Предпочитая
- 15. Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.
- 16. Симметрия
- 17. Симметрия (греч.) - соразмерность, пропорциональность, одинаковость в расположении частей.
- 18. Фигуры, обладающие осевой симметрией
- 19. КАКИЕ ИЗ ЭТИХ ФИГУР ИМЕЮТ ОСЬ СИММЕТРИИ?
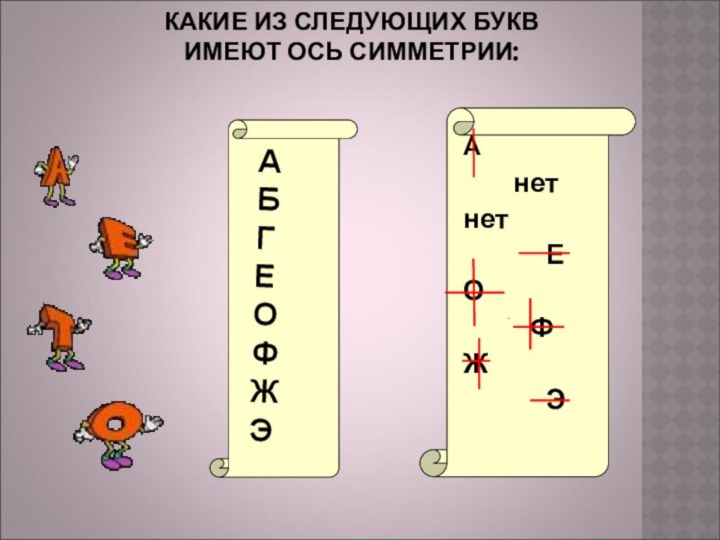
- 22. КАКИЕ ИЗ СЛЕДУЮЩИХ БУКВ ИМЕЮТ ОСЬ
- 24. СИММЕТРИЯ В БАЛЕТЕЗнаменитые фуэте, когда балерина вращается
- 26. Геометрия владеет двумя сокровищами, одно из них
- 27. Имел красивую внешность, носил длинную бороду, а
- 28. ТЕОРЕМА ПИФАГОРАПребудет вечной истина, как скороЕё познает
- 29. ФОРМУЛИРОВКА ТЕОРЕМЫВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
- 30. abcbabaaccc12?b
- 31. Если дан нам треугольник,И притом с прямым
- 32. Учащиеся средних веков считали доказательство теоремы очень
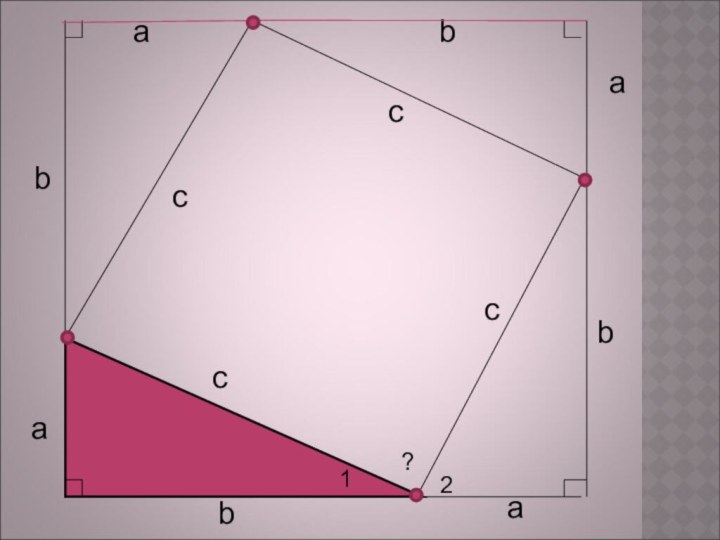
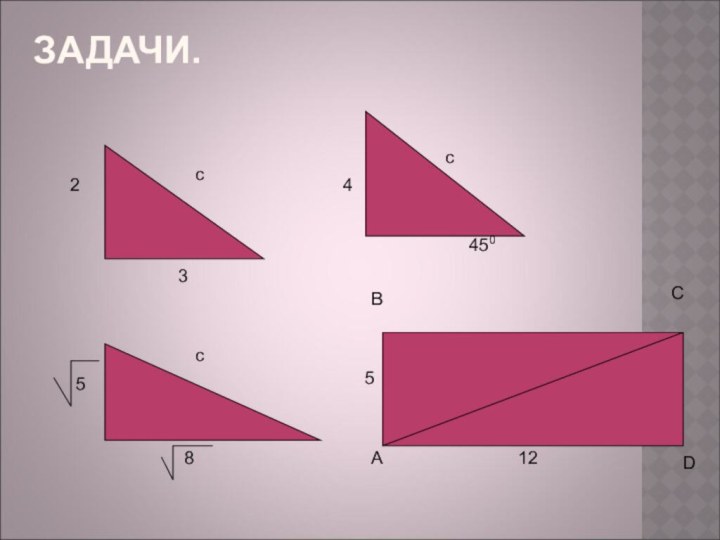
- 33. ЗАДАЧИ.23c458cc512ABCD450
- 34. ЗОЛОТОЕ СЕЧЕНИЕ - это такое
- 35. Деление отрезка в золотом отношении Дано: отрезок
- 36. Золотой треугольникАВСЗолотым называется такой равнобедренный треугольник, основание
- 37. Золотой прямоугольникПрямоугольник, стороны которого находятся в золотом
- 38. Золотое сечение и золотая спиральВ биологических исследованиях
- 39. Рассмотрим побег цикория. От основного стебля образовался
- 40. Тело мужчины ближе к идеалу, чем женщины.
- 41. У многих бабочек соотношение размеров грудной и
- 42. Переходя к примерам золотого сечения в живописи,
- 43. Ярким примером применения золотого сечения в архитектуреявляется
- 44. Скачать презентацию
- 45. Похожие презентации



























Слайд 2
Объект математики - весь мир,
и его изучают
все остальные науки.
доступность, естественным образом проникают на урок элементы занимательности.
Слайд 4
Цели урока:
1. Образовательная: познакомить и научить учащихся построению
некоторых правильных многоугольников с помощью циркуля и линейки.
2. Развивающая:
формировать научное мировоззрение и пространственное воображение учащихся.3. Воспитательная: выработать внимание и самостоятельность при работе на уроке.
ТЕМА : ПОСТРОЕНИЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ
Ход урока
Сегодня у нас не обычный урок, а интегрированный, то есть вас будут учить одновременно два учителя: геометрии и черчения. Таким образом, мы попробуем проследить аналогию между этими предметами.
2. Актуализация знаний учащихся.
Учитель геометрии. Какой многоугольник называется правильным? (Ответы учащихся)
Запишите на доске все формулы, изученные на прошлом уроке. (Запись формул на доске)
Учитель черчения. Какие геометрические построения вам известны? (Ответы учащихся)
3. Изучение новой темы.
Учитель геометрии. Тема нашего урока:«Построение правильных многоугольников».
Учитель черчения. Название темы, которую предлагаю вам я: «Деление окружности
на равные части».
Слайд 5
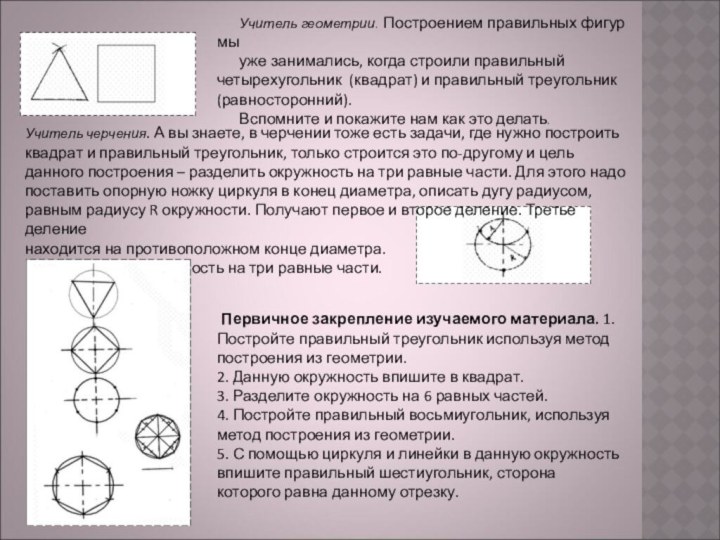
Учитель геометрии. Построением правильных фигур мы
уже занимались,
когда строили правильный четырехугольник (квадрат) и правильный треугольник (равносторонний).
Вспомните и покажите нам как это делать.
Учитель черчения. А вы знаете, в черчении тоже есть задачи, где нужно построить квадрат и правильный треугольник, только строится это по-другому и цель данного построения – разделить окружность на три равные части. Для этого надо поставить опорную ножку циркуля в конец диаметра, описать дугу радиусом, равным радиусу R окружности. Получают первое и второе деление. Третье деление
находится на противоположном конце диаметра.
Мы разделили окружность на три равные части.
Первичное закрепление изучаемого материала. 1.Постройте правильный треугольник используя метод построения из геометрии.
2. Данную окружность впишите в квадрат.
3. Разделите окружность на 6 равных частей.
4. Постройте правильный восьмиугольник, используя метод построения из геометрии.
5. С помощью циркуля и линейки в данную окружность впишите правильный шестиугольник, сторона которого равна данному отрезку.
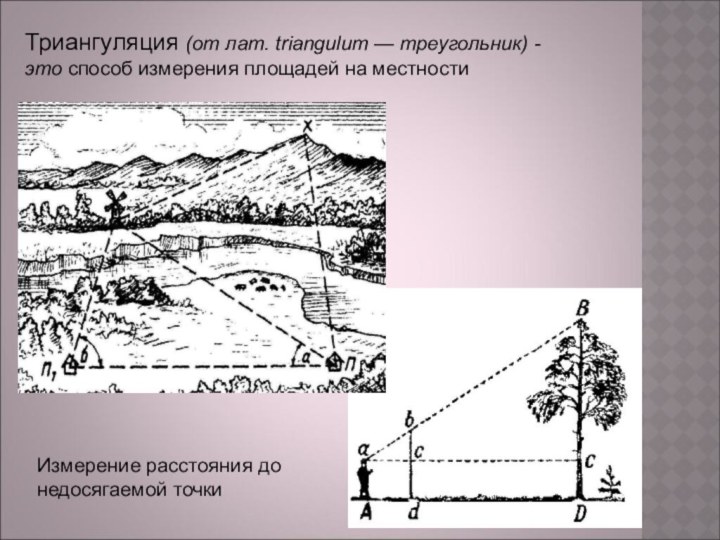
Слайд 7 Триангуляция (от лат. triangulum — треугольник) - это способ
измерения площадей на местности
Измерение расстояния до недосягаемой точки
Слайд 9
Примеры задач на применение
векторных величин
Тест с выбором
ответа
1. Что такое вектор?
а) вектор - это направленный отрезок;
б)
вектор - это отрезок имеющий координаты;
в) вектор – это прямая, имеющая направление.2.Что такое нулевой вектор?
а) вектор, абсолютная величина которого не существует;
б) вектор, у которого начало совпадает с его концом;
в) вектор, не имеющий ни начала, ни конца.
3. Какие векторы называются равными?
а) два вектора называются равными, если они не совмещаются параллельным переносом;
б) два вектора называются равными, если они совмещаются параллельным переносом;
в) два вектора называются равными, если они одинаково направлены.
Слайд 10
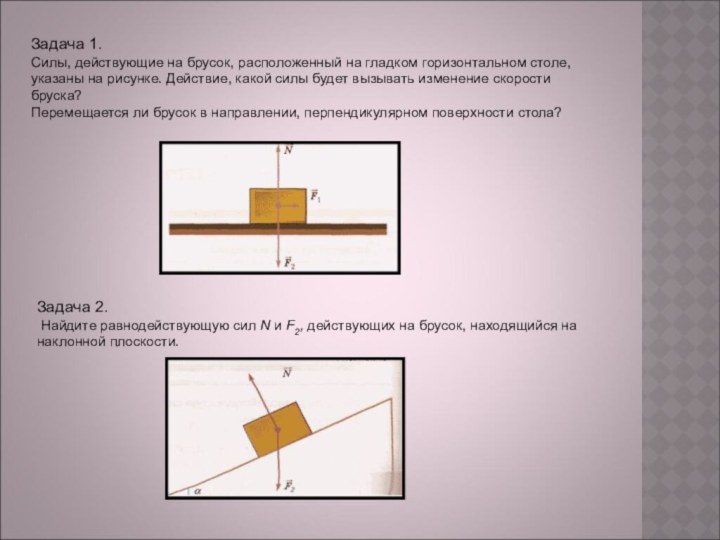
Задача 1.
Силы, действующие на брусок, расположенный на гладком
горизонтальном столе,
указаны на рисунке. Действие, какой силы будет
вызывать изменение скорости бруска? Перемещается ли брусок в направлении, перпендикулярном поверхности стола?
Задача 2.
Найдите равнодействующую сил N и F2, действующих на брусок, находящийся на наклонной плоскости.
Слайд 11
Задание «Эксперементальное»
На узелок действуют три силы, две
из которых образуют
угол в 60°, направленные вверх. Третья
сила направлена вниз. Почему узелок находится в покое?
Чему равна равнодействующая сил 1 и 2?
Груз какой массы подвешен вниз?
Задача. Если на тело могут действовать 2 силы,
направленные под углом 90°, (Сложение неколлинеарных векторов), то равнодействующая этих сил находится по правилу параллелограмма,
а ее модуль – по теореме Пифагора.
Если к телу приложены две равные по модулю и противоположные по направлению силы, то равнодействующая равна нулю, а тело находится в покое.
Слайд 12 1. В бассейне с горизонтальным дном площадью 1
га содержится 10 миллионов литров воды. Можно ли в
этом бассейне провести соревнования по плаванию? ( Высота слоя воды 1 дм.)2. Смекалкин спросил младшего брата: «Какой объем имеет 1 лист бумаги?». Брат удивился: «Разве у листа бумаги может быть объем?» Смекалкин дал ему 300 листов бумаги, сложенных в пачку и предложил использовать ее для вычисления объема листа. Длина пачки 300 мм, ширина 203 мм, высота 30 мм. Найдите объем одного листа. (Объем равен 6090 кубических миллиметров.)
3. В некотором царстве, в некотором государстве была такая единица длины – бумбас. Двор царского дворца имел форму прямоугольника со сторонами 50 и 80 бумбасов. Найдите площадь дворца в квадратных бумбасах. (4000(кв.бумбасов).)
А сам дворец стоял в углу двора, занимал квадрат со стороной 20 бумбасов. Царь решил выложить двор снаружи коврами, имевшими форму прямоугольников со сторонами 2 и 5 бумбасов. Сколько потребуется ковров? (360 ковров.)
ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ
Слайд 13
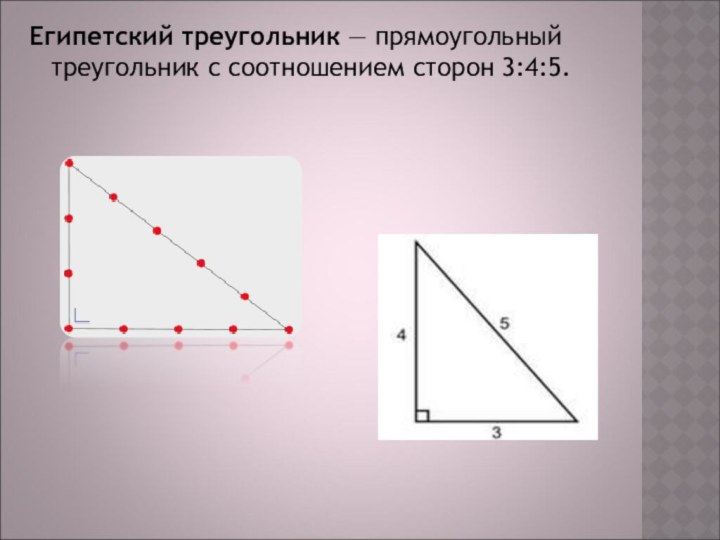
ЕГИПЕТСКАЯ ПИРАМИДА
Если сложить четыре стороны основания
пирамиды, мы получим для ее обвода 931,22 метра. Разделив
же это число на удвоенную высоту (2 × 148,208) имеем в результате 3,1416, т.е. отношение длины окружности к диаметру. Этот единственный в своем роде памятник представляет собою, следовательно, материальное воплощение числа «пи», игравшего столь важную роль в истории математики.
Слайд 14
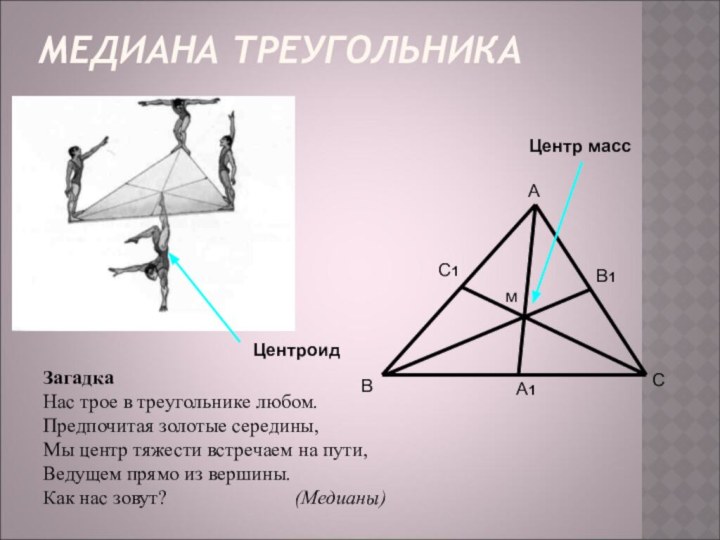
МЕДИАНА ТРЕУГОЛЬНИКА
Центр масс
м
А
В
С
А1
С1
В1
Центроид
Загадка
Нас трое в треугольнике любом.
Предпочитая золотые
середины,
Мы центр тяжести встречаем на пути,
Ведущем прямо из
вершины.Как нас зовут? (Медианы)
Слайд 19
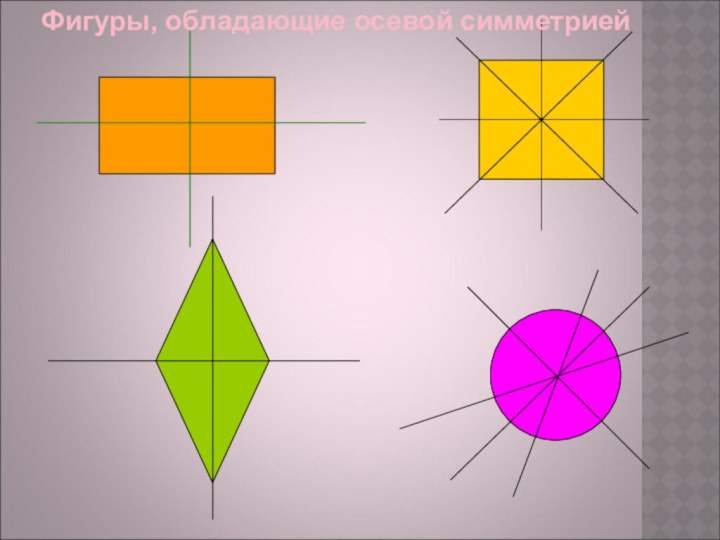
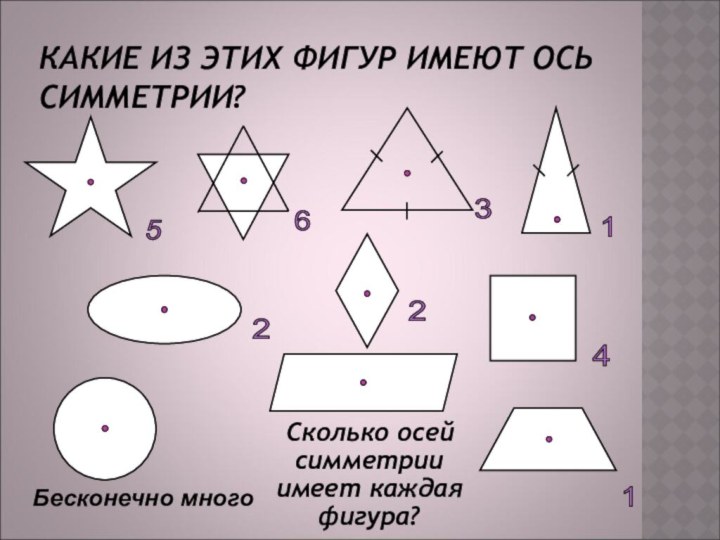
КАКИЕ ИЗ ЭТИХ ФИГУР ИМЕЮТ ОСЬ СИММЕТРИИ?
Сколько осей симметрии имеет каждая фигура?
5
6
3
1
1
2
2
4
Бесконечно много
Слайд 24
СИММЕТРИЯ В БАЛЕТЕ
Знаменитые фуэте, когда балерина вращается на
одной ножке 6 раз, 12, …, 32 раза! Их
повторяемость рождает эстетический эффект, служащий достойным завершением танца
Слайд 26
Геометрия владеет двумя сокровищами, одно из них –
это теорема Пифагора,
а другое –
деление отрезка
в
среднем и крайнем отношении. Первое можно представить мерой золота;
второе же больно напоминает драгоценный камень.
Иоганн Кеплер
Слайд 27 Имел красивую внешность, носил длинную бороду, а на
голове золотую диадему.
Много путешествовал, учился у древних философов Анаксимандра
и Ферекида.В г. Кротон на юге Италии учредил философское общество- Пифагорейский союз.
Пифагор - это не имя !
Так прозвали философа
за умение говорить
убедительно («пифагорус» -
утверждающий речью ).
Слайд 28
ТЕОРЕМА ПИФАГОРА
Пребудет вечной истина, как скоро
Её познает слабый
человек!
И ныне теорема Пифагора
Верна, как и в его далёкий
век.Обильно было жертвоприношение
Богам от Пифагора. Сто быков
Он отдал на закланье и сожжение
За света луч, пришедший с облаков.
А. Шамиссо
Слайд 29
ФОРМУЛИРОВКА ТЕОРЕМЫ
В прямоугольном треугольнике
квадрат гипотенузы равен
сумме
квадратов катетов.
Слайд 31
Если дан нам треугольник,
И притом с прямым углом,
То
квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней
находим – И таким простым путем
К результату мы придем!
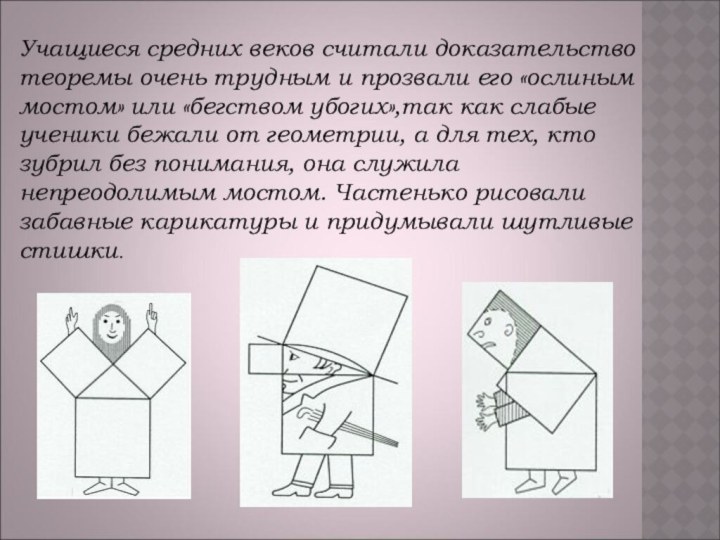
Слайд 32 Учащиеся средних веков считали доказательство теоремы очень трудным
и прозвали его «ослиным мостом» или «бегством убогих»,так как
слабые ученики бежали от геометрии, а для тех, кто зубрил без понимания, она служила непреодолимым мостом. Частенько рисовали забавные карикатуры и придумывали шутливые стишки.
Слайд 34
ЗОЛОТОЕ СЕЧЕНИЕ
- это такое пропорциональное
деление отрезка на неравные части, при котором весь отрезок
так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему отрезку.
Слайд 35
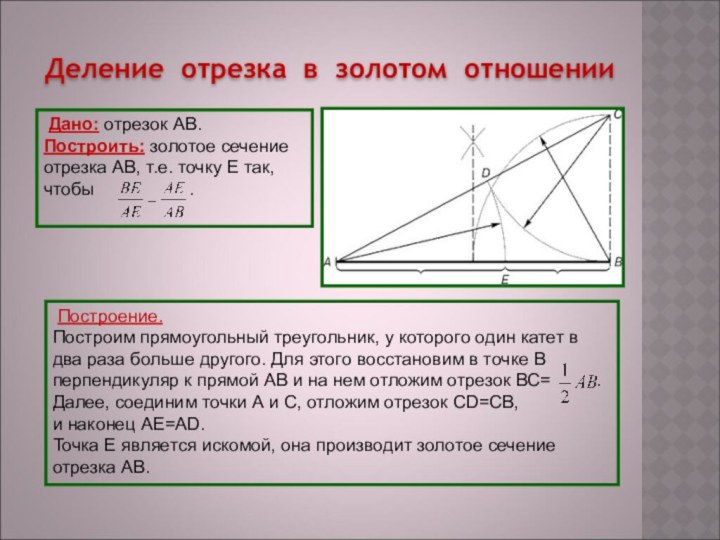
Деление отрезка в золотом отношении
Дано: отрезок АВ.
Построить:
золотое сечение отрезка АВ, т.е. точку Е так, чтобы
. Построение.
Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок ВС= .
Далее, соединим точки А и С, отложим отрезок CD=CB,
и наконец AE=AD.
Точка Е является искомой, она производит золотое сечение отрезка АВ.
Слайд 36
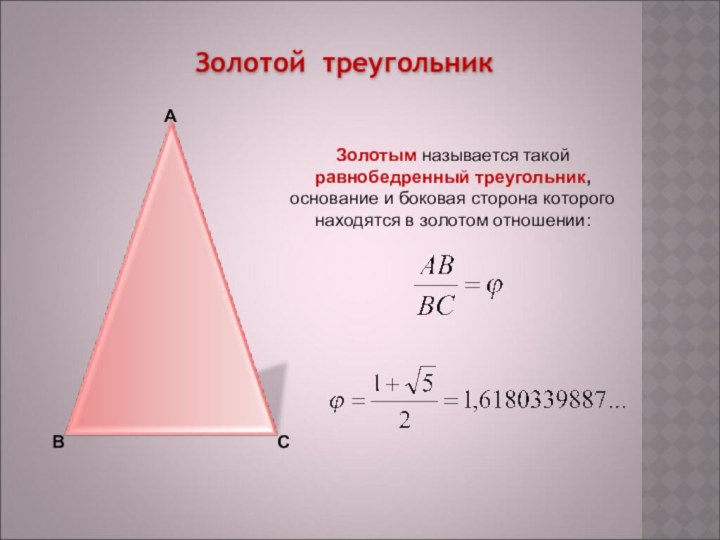
Золотой треугольник
А
В
С
Золотым называется такой равнобедренный треугольник, основание и
боковая сторона которого находятся в золотом отношении:
Слайд 37
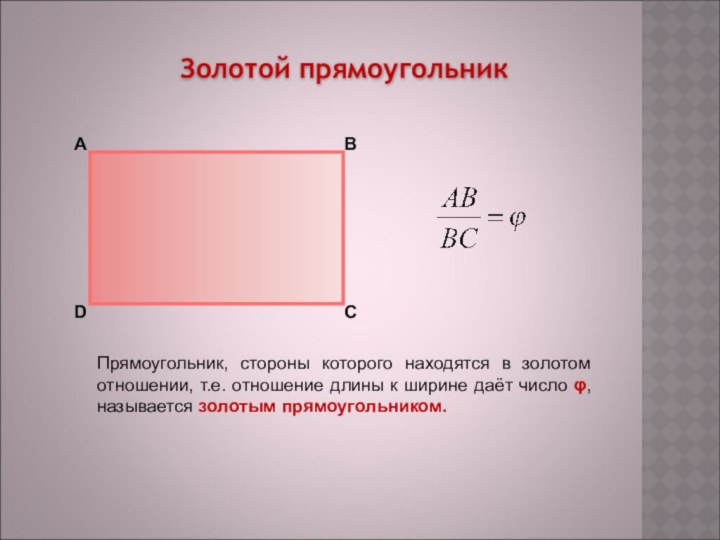
Золотой прямоугольник
Прямоугольник, стороны которого находятся в золотом отношении,
т.е. отношение длины к ширине даёт число φ, называется
золотым прямоугольником.А
В
С
D
Слайд 38
Золотое сечение и золотая спираль
В биологических исследованиях было
показано, что, начиная с вирусов и растений и кончая
организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.Было установлено, что числовой ряд чисел Фибоначчи характеризует структурную организацию многих живых систем. Например, винтовое листорасположение на ветке составляет дробь (число оборотов на стебле/число листьев в цикле, напр. 2/5; 3/8; 5/13), соответствующую рядам Фибоначчи.
Хорошо известна "золотая" пропорция пятилепестковых цветков яблони, груши и многих других растений. Носители генетического кода - молекулы ДНК и РНК - имеют структуру двойной спирали; ее размеры почти полностью соответствуют числам ряда Фибоначчи.
Гете подчеркивал тенденцию природы к спиральности.
Паук плетет паутину спиралеобразно.
Спиралью закручивается ураган.
Испуганное стадо северных оленей
разбегается по спирали.
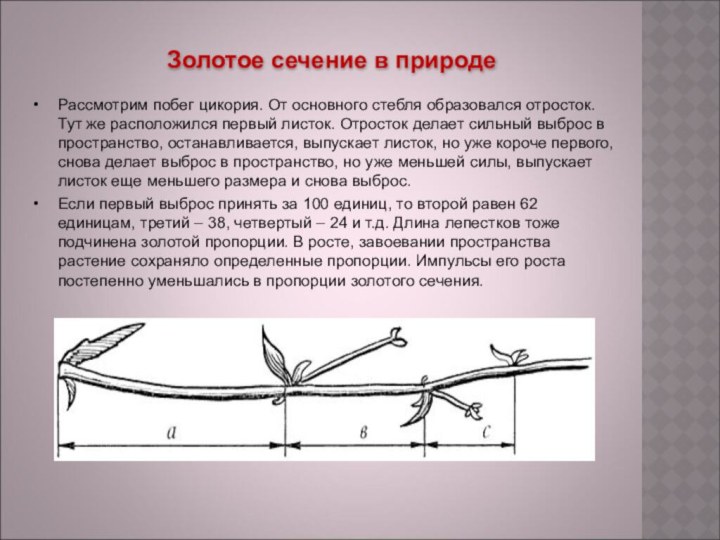
Слайд 39 Рассмотрим побег цикория. От основного стебля образовался отросток.
Тут же расположился первый листок. Отросток делает сильный выброс
в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс.Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.
Золотое сечение в природе
Слайд 40 Тело мужчины ближе к идеалу, чем женщины. Чтобы
приблизиться к идеалу, женщины надевают туфли на каблуках. Деление
тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к пропорциям золотого сечения, чем пропорции женского тела, в отношении которого среднее значение выражается в соотношении 8 : 5 = 1,6.Слайд 41 У многих бабочек соотношение размеров грудной и брюшной
части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка
образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.В ящерице длина ее хвоста так относится к длине остального тела, как 62 к 38. Можно заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.
Золотое сечение в природе
Слайд 42 Переходя к примерам золотого сечения в живописи, нельзя
не остановить своего внимания на творчестве Леонардо да Винчи.
Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды».Портрет Моны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника.
ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОПИСИ





























