- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Уравнения
Содержание
- 2. Что такое уравнение ?Уравнение – это равенство двух функций, содержащих один или несколько аргументов.
- 3. Немного истории…
- 4. Иероглифическая запись уравненияМатематика в Древнем Египте«Число и
- 5. Математика в Древнем ЕгиптеНеизвестное число - „хау“,
- 6. Решение: В папирусе Ахмеса
- 7. Часть страницы из алгебры Бхаскары «Видиса
- 8. 6x -13 = 5x - 86x +
- 9. Основное произведение Диофанта — Арифметика в 13 книгах. Арифметика ДиофантаЛист
- 10. Знак равенства в современной форме создал математик Роберт
- 11. Создателем современной буквенной символики является французский математик
- 12. Где используются уравнения сегодня?
- 13. Химия
- 14. Уравнение, описывающее количество кроликов, скорость размножения которых
- 15. ЭкономикаУравнение экономического равновесияY=C+Ig+G+Xn+S=P×QS =ВВП=P×QD =M×VУравнение «доходы - расходы» имеет следующий вид:R + S = C + Ig + IG + G + XE – Xi + S = YC + Yg + YG + N + AСовокупное предложение определяется по формуле:PQS = R + S =
- 16. ФизикаУравнение состояния идеального газа:Уравнение равномерного прямолинейного движения
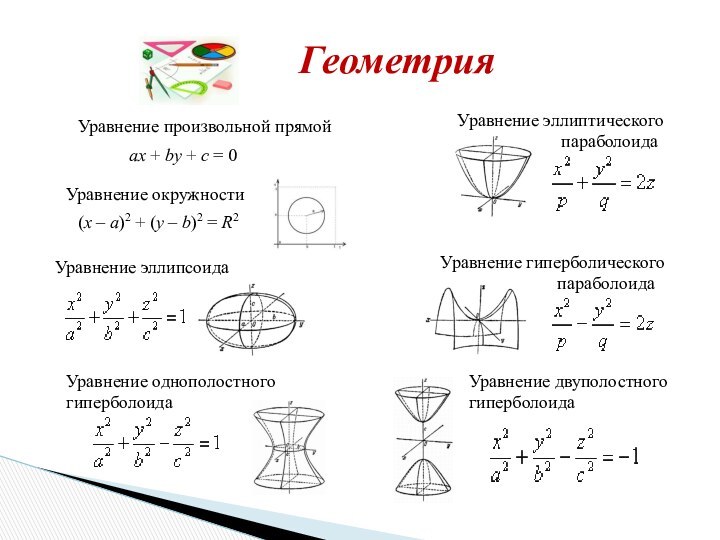
- 17. Геометрияax + by + c = 0 Уравнение произвольной прямой Уравнение окружности(x – a)2 + (y – b)2 = R2Уравнение эллипсоидаУравнение однополостного
- 18. АлгебраЛинейное уравнение ax
- 19. Способы решения уравнений
- 20. Аналитический способа) Решить уравнение: 18х2
- 21. Алгебраический способРешить уравнение:Решение:Ответ:
- 22. Графический способОпределить число решений уравнения |x +
- 23. «Никогда не считай, что ты знаешь всё, что тебе уже больше нечему учиться».Н.Д. ЗелинскийУдачи!
- 24. Скачать презентацию
- 25. Похожие презентации
Что такое уравнение ?Уравнение – это равенство двух функций, содержащих один или несколько аргументов.
Слайд 2
Что такое уравнение ?
Уравнение – это равенство двух
функций, содержащих один или несколько аргументов.
Слайд 4
Иероглифическая запись уравнения
Математика в Древнем Египте
«Число и его
половина составляют 9. Найти число.»
Одна из задач Московского папируса:
Современная
запись решения:(около 1850 г. до н. э.)
Московский папирус
Слайд 5
Математика в Древнем Египте
Неизвестное число - „хау“, “куча”
или “неизвестное
количество” единицЗадача из сборника Ахмеса:
«Куча и ее четвертая часть дают вместе 15. Найти кучу».
Запись задачи нашими
знаками:
Часть папируса Ахмеса. 1650г. до н.э.
Слайд 6
Решение:
В папирусе Ахмеса решение
начинается так:
«Считай с 4; от них ты должен
взять четверть. А именно 1 и 4 вместе 5». Затем 15 делится на 5, частное умножается на 4 и получается неизвестное 12.« метод ложного положения ».
Слайд 7 Часть страницы из алгебры Бхаскары «Видиса Ганита»
VII век
(вычисление корней)Математика в Древней Индии
х2- 64х = - 768
х2 - 64х + 322 = -768+ 322
(х - 32)2 = 256,
х - 32 = ±16,
х1= 16, х2 = 48.
Слайд 8
6x -13 = 5x - 8
6x + 8
= 5x+13
х = 5
«ал-мукабала» и «ал-джабр»
Математика исламского средневековья
"ал-джабр"
"ал-мукабала"
6x
- 5х = 13 - 8
Слайд 9
Основное произведение Диофанта — Арифметика в 13 книгах.
Арифметика Диофанта
Лист из Арифметики (рукопись
XIV века). В верхней строке записано уравнение:
Например, уравнение
202x2 + 13 – 10x = 13он записывает так:
Слайд 10 Знак равенства в современной форме создал математик Роберт Рекорд
в 1557 году.
Появление символа равенства
Первое печатное появление знака равенства
в книге Роберта Рекорда в1557 году (записано уравнение )
Слайд 11
Создателем современной буквенной символики является французский математик
Франсуа
Виет (1540 – 1603).
ax + b = 0
ax2 + bx + c = 0ax4 + bx2 + c = 0
ax + by + c = 0
Появление буквенной символики
Слайд 14 Уравнение, описывающее количество кроликов, скорость размножения которых тем
больше, чем больше их
уже родилось
Процессы рапространения волн в сердечной
мышце, образование пятен планктона в океане, формообразования окраски шкур животныхБиология
Слайд 15
Экономика
Уравнение экономического равновесия
Y=C+Ig+G+Xn+S=P×QS =ВВП=P×QD =M×V
Уравнение «доходы - расходы» имеет следующий вид:
R + S = C + Ig + IG + G + XE – Xi + S = YC + Yg + YG + N + A
Совокупное предложение определяется по формуле:
PQS = R + S = C
+ Ig + IG + G + XE – Xi + S =
BHП.Совокупный спрос равен:
PQD = YC + Yg + YG + N + A = Y = M∙V = BHП.
R (x, z) = Y (y, z) = MА∙V (x, y) = R (Y, MА) = Y (R, MА) = MА∙V (R, Y).
Слайд 16
Физика
Уравнение состояния идеального газа:
Уравнение равномерного прямолинейного движения :
Первый
закон термодинамики:
Закон всемирного тяготения:
F = GMm/D2
Закон Кулона:
Закон Ома для замкнутой цепи:
Слайд 17
Геометрия
ax + by + c = 0
Уравнение произвольной прямой
Уравнение окружности
(x – a)2 + (y – b)2 = R2
Уравнение эллипсоида
Уравнение однополостного
гиперболоида
Уравнение
эллиптического
параболоидаУравнение двуполостного
гиперболоида
Уравнение гиперболического
параболоида
Слайд 18
Алгебра
Линейное уравнение
ax +
b = 0
Квадратное уравнение
ax2 + bx +
c = 0Кубическое уравнение
ax3 + bx2 + cx + d = 0
Виды алгебраических уравнений
Биквадратное уравнение
ax4 + bx2 + c = 0
Возвратное уравнение
ax4 + bx3 + cx2 + bx + a = 0
Показательное уравнение
af(x) = b или af(x) = ag(x) (a > 0; a ≠ 1)
Логарифмическое уравнение
loga f(x) = loga g(x), (a > 0, a ≠ 1)
Тригонометрическое уравнение
sin x = a; cos x = a; tg x = a
Иррациональное уравнение
или
Параметрическое уравнение
|f (x)| + |g (x)| = a
Слайд 22
Графический способ
Определить число решений уравнения |x + 1|
+ |x + 2| = a в зависимости от
параметра а.Решение:
График функции y = |x + 1| + |x + 2| будет представлять собой ломаную.
Ее вершины будут располагаться в точках (-2; 1) и (-1; 1).
Ответ: если параметр a <1, то корней у уравнения не будет;
если а = 1, то решением уравнения является бесконечное множество чисел из отрезка [-2; -1];
если a >1, то уравнение будет иметь два корня.
Слайд 23 «Никогда не считай, что ты знаешь всё, что
