- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Паркеты: музыка для глаз
Содержание
- 2. ПАРКЕТЫ:МУЗЫКА ДЛЯ ГЛАЗ
- 3. СОДЕРЖАНИЕ РАБОТЫЗамощение.Построение орнаментов.Паркеты.Виды паркетов.Алгоритм построения паркетов.
- 4. Замощéние — разбиение плоскости или пространства
- 5. Построить орнамент – это тоже самое, что
- 6. Паркеты Замощения плоскости одинаковыми многоугольниками, которые не пересекают
- 7. Слово "паркет" появилось во Франции. Там
- 8. Паркет – это покрытие плоскости многоугольниками без пропусков и наложений.
- 9. Паркет получится в трёх случаях: из правильных
- 10. 4. при n =6, m =360:120=3 шестиугольника.При
- 11. Виды паркетов
- 12. Немного теории… В энциклопедическом словаре юного математика написано,
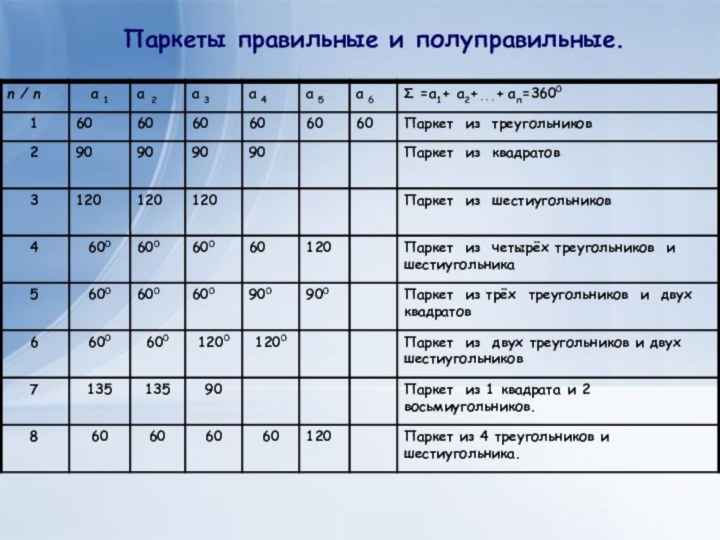
- 13. Паркеты правильные и полуправильные.
- 14. 1. Рисуем выбранный многоугольник.2. Копируем.3. Полученную копию
- 15. Оказывается можно сделать элементом
- 16. Небольшое отступление…
- 17. Искусство орнамента содержит в неявном виде
- 18. БОРДЮРЫ. Бордюром называют плоскую геометрическую фигуру, характеризующуюся векторами
- 19. ПОСТРОЕНИЕ БОРДЮРОВПри построении бордюров сначала:строят одну ячейку,затем
- 20. В журнале «Квант» за 1979 год в
- 21. ПРИМЕРЫ БОРДЮРОВАвторы Киреева Ксения Конова ЕкатеринаДобродий ЕлиизаветаБордюры с http://janr.perm.ru
- 22. Розе́тта в архитектуре (от фр. rosette, буквально
- 23. Паркет (франц. parquet), небольшие древесные, строганные планки
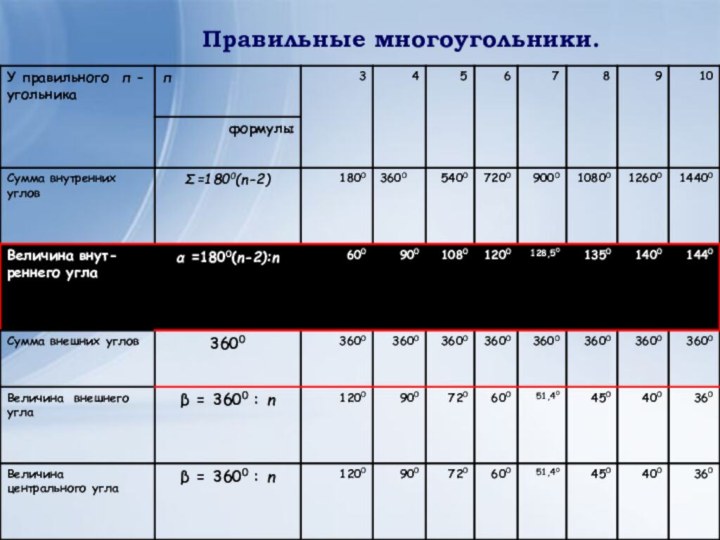
- 24. Правильные многоугольники.
- 25. Их особенность в том, что в каждом
- 26. В зависимости от набора
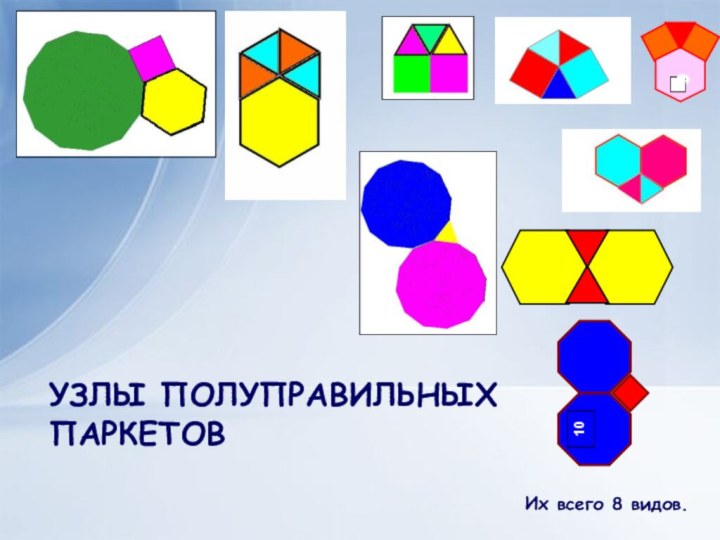
- 27. УЗЛЫ ПОЛУПРАВИЛЬНЫХ ПАРКЕТОВИх всего 8 видов.
- 29. Все мои произведения — это игрыСерьёзные игры.М. ЭшерС помощью работ
- 30. Морис Эшер родился в городе Лёвардене нидерландской
- 31. Скачать презентацию
- 32. Похожие презентации























Слайд 3
СОДЕРЖАНИЕ РАБОТЫ
Замощение.
Построение орнаментов.
Паркеты.
Виды паркетов.
Алгоритм построения паркетов.
Слайд 4 Замощéние — разбиение плоскости или пространства на
фигуры без общих внутренних точек.
Существует мнение, что впервые интерес к замощению возник в связи с построением мозаик, орнаментов и других узоров.
Слайд 5
Построить орнамент – это тоже самое, что и
замостить плоскость.
В каждом из этих замощений любые два
многоугольника имеют:либо общую сторону,
либо только общую вершину,
или совсем не имеют общих точек.
Построение орнамента
Подробно об орнаментах
Слайд 6
Паркеты
Замощения плоскости одинаковыми многоугольниками, которые не пересекают друг
друга и не оставляют пустого пространства называют паркетами.
Плоскость
заполняется сдвигами одного и того же рисунка на два вектора (в горизонтальном и вертикальном направлениях). подробнее
Слайд 7
Слово "паркет" появилось во Франции. Там впервые
начали изготавливать щитовой и мозаичный пол из древесины.
В России активно использовать паркет начали лишь в XVIII веке, во время строительства Эрмитажа. Ранее для настила пола применяли в основном толстые половицы из мягких пород древесины: сосны, ели, лиственницы.
Наибольшее распространение на Руси получили пол из деревянных досок (так называемых "деревянных кирпичей") и художественный паркет.
Происхождение слова «паркет».
Авторы Конова Е.
Киреева К.
Автор Добродий Е..
Слайд 9
Паркет получится в трёх случаях: из правильных
треугольников,
правильных четырехугольников, правильных шестиугольников.
Главное условие построения паркетов.
Сумма
углов многоугольников в узле паркета(в общей вершине n-угольников) 360°.
Доказательство:
Вычислить количество правильных n-угольников около общей вершины можно по формуле m ═ 360:α, где m - количество n-угольников, α – величина внутреннего угла в градусах.
1. При n=3, m=360:60=6 треугольников в узле.
2. При n=4, m=360:90=4 четырёхугольника в узле.
3. При n=5, m=360:108=3,333333…
Но количество n -угольников не может быть дробным числом, число многоугольников - это число натуральное.
Слайд 10
4. при n =6, m =360:120=3 шестиугольника.
При n≥7
внутренние углы правильных n-угольников больше 120°. Кроме того, внутренние
углы правильного многоугольника всегда меньше 180 ° .120 °<α<180 °
Из двух дробей с одинаковыми числителями та дробь больше, у которой знаменатель меньше. Поэтому,
360:120>360:α>360:180 ,
2<360:α<3,
2
Вывод: для n≥7 не существует правильных многоугольников, для которых бы выполнялось главное условие. Значит, паркет из этих многоугольников (n≥7) построить нельзя!
Используя данные выделенной строчки таблицы «Правильные многоугольники» можно ещё раз убедиться в сделанном выводе.
Слайд 12
Немного теории…
В энциклопедическом словаре юного математика написано, что
существует всего 11 паркетов, которые состоят из одинаковых узлов
правильных n - угольников, но доказательства этого приведено не было.Зато это доказательство было найдено нами, коротко результаты её исследования можно представить в виде таблицы
Посмотрите таблицу!
Слайд 14
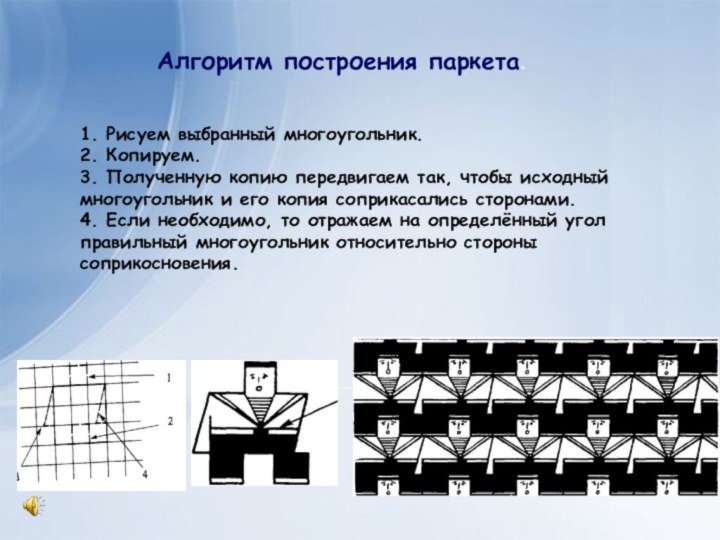
1. Рисуем выбранный многоугольник.
2. Копируем.
3. Полученную копию передвигаем
так, чтобы исходный многоугольник и его копия соприкасались сторонами.
4. Если необходимо, то отражаем на определённый угол правильный многоугольник относительно стороны соприкосновения.
Алгоритм построения паркета.
Слайд 15
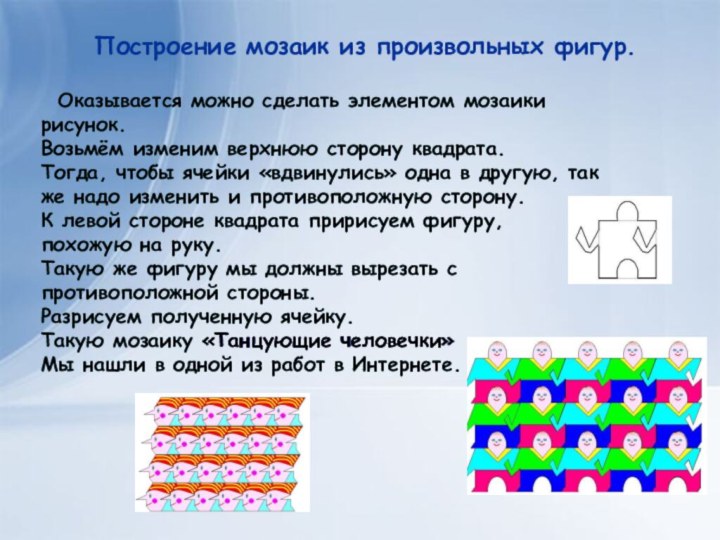
Оказывается можно сделать элементом мозаики рисунок.
Возьмём
изменим верхнюю сторону квадрата. Тогда, чтобы ячейки «вдвинулись» одна в
другую, также надо изменить и противоположную сторону. К левой стороне квадрата пририсуем фигуру,
похожую на руку. Такую же фигуру мы должны вырезать с противоположной стороны. Разрисуем полученную ячейку. Такую мозаику «Танцующие человечки»
Мы нашли в одной из работ в Интернете.
Построение мозаик из произвольных фигур.
Оказывается можно сделать элементом мозаики рисунок.
Возьмём изменим верхнюю сторону квадрата.
Тогда, чтобы ячейки «вдвинулись» одна в другую, так
же надо изменить и противоположную сторону.
К левой стороне квадрата пририсуем фигуру,
похожую на руку.
Такую же фигуру мы должны вырезать с противоположной стороны.
Разрисуем полученную ячейку.
Такую мозаику «Танцующие человечки»
Мы нашли в одной из работ в Интернете.
Слайд 17
Искусство орнамента содержит
в неявном виде
наиболее древнюю
часть известной нам
высшей
математики.
Г.Вейль
Орнамент (от лат. оrnаmеntum -
украшение) - это узор, состоящий из повторяющихся, ритмически упорядоченных элементов. Орнамент предназначен для украшения различных предметов (посуды, мебели, текстильных изделий, оружия) и архитектурных сооружений.
Он выявляет и подчёркивает своим построением, формой и цветом архитектурные и
конструктивные особенности предмета, природную красоту материала.
Слайд 18
БОРДЮРЫ.
Бордюром называют плоскую геометрическую фигуру, характеризующуюся векторами а
и nа (где n - целое число), при которых
эта фигура переходит в себя, но не переходит в себя при параллельных переносах , иного вида.Вектор а - направляющий для бордюра.
Бордюр — кромка, кайма, обрамление (франц. bordure, от bord — край).
Ленточные орнаменты – это бордюры.
Слайд 19
ПОСТРОЕНИЕ БОРДЮРОВ
При построении бордюров сначала:
строят одну ячейку,
затем задают
вектор (направленный отрезок), на который будет сдвинута фигура,
параллельным переносом
сдвигают ячейку вправо на длину заданного вектора 1-2 во столько раз, сколько необходимо.
Слайд 20
В журнале «Квант» за 1979 год в статье
А.Землякова «Орнаменты» есть атлас орнаментов.
Оси симметрии отмечены пунктиром,
центры
поворотов обведены кружком, а в скобках указаны углы поворотов;
стрелками показаны параллельные переносы.
Если добавить к этим орнаментам еще два, то получится полный «атлас» плоских орнаментов.
Оказывается, существует только
17 различных типов орнаментов.
Атлас орнаментов.
Слайд 21
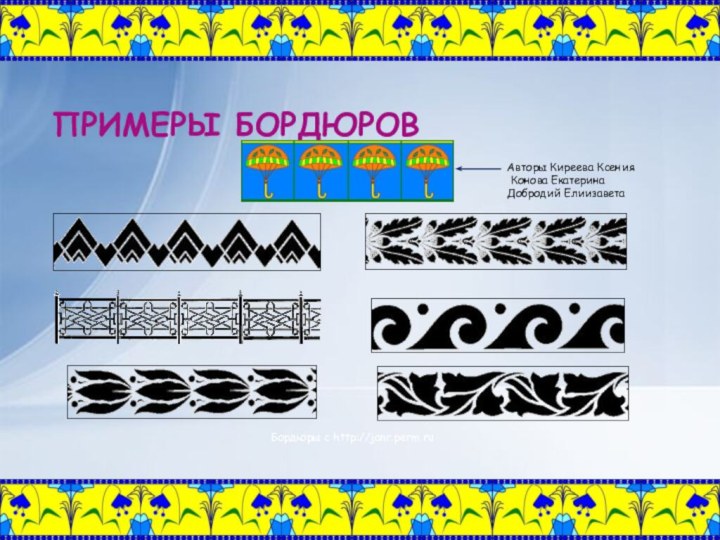
ПРИМЕРЫ БОРДЮРОВ
Авторы Киреева Ксения
Конова Екатерина
Добродий Елиизавета
Бордюры с
http://janr.perm.ru
Слайд 22
Розе́тта в архитектуре (от фр. rosette, буквально «розочка»;
иначе розетка) — мотив орнаментации, представляющий собой заключённые в
круге четыре или несколько лепестков цветка или листьев, одинаковых по форме, расположенных симметрично и как бы исходящих из одной центральной пуговки.Розетты.
Фото http://commons.wikimedia.org/wiki/Category:Rosette_(Ornament)
Слайд 23
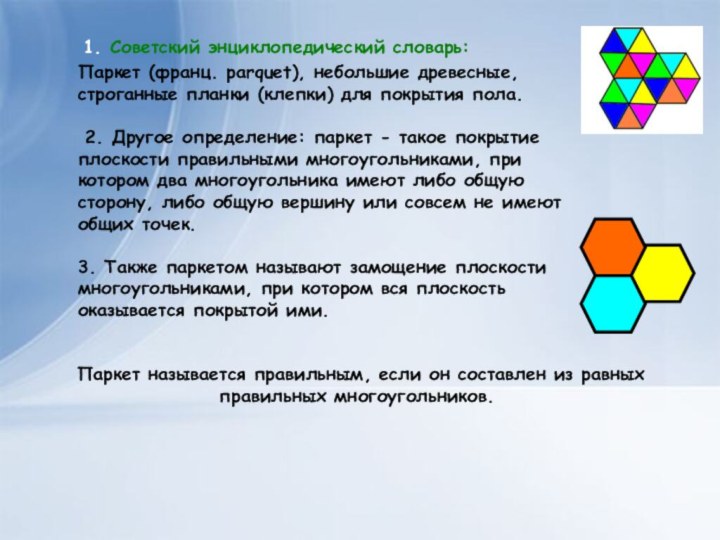
Паркет (франц. parquet), небольшие древесные, строганные планки (клепки)
для покрытия пола.
2. Другое определение: паркет -
такое покрытие плоскости правильными многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину или совсем не имеют общих точек.3. Также паркетом называют замощение плоскости многоугольниками, при котором вся плоскость оказывается покрытой ими.
1. Советский энциклопедический словарь:
Паркет называется правильным, если он составлен из равных правильных многоугольников.
Слайд 25
Их особенность в том, что в каждом из
них участвуют правильные многоугольники одного вида и «звёзды» в
каждом узле такой мозаики одинаковы (звезда – это какой-либо узел и все примыкающие к нему многоугольники).Правильные паркеты
Слайд 26
В зависимости от набора многоугольников
в каждой вершине возможны три случая.
1. Три одинаковых многоугольника.
2.
Два одинаковых и один отличный от них.3. Три различных многоугольника.
Полуправильные паркеты
(из неравных правильных
многоугольников)
Если снять ограничение о том, что в покрытии участвуют только одинаковые правильные многоугольники, но сохранить условие, что все звёзды в покрытии «устроены одинаково», то полученные покрытия плоскости часто называются полуправильными мозаиками (или паркетами).
Слайд 29
Все мои произведения — это игры
Серьёзные игры.
М. Эшер
С помощью работ Мориса
Эшера можно объяснить такие математические понятия и термины, изучаемые
в школе, как: параллельный перенос, подобие фигур, равновеликие фигуры, периодичность. А так же некоторые понятия, не входящие в школьный курс математики.Самым интересным с точки зрения математики является замощение плоскости или мозаики. Известно много орнаментов, составленных из повторяющихся мотивов.
Слайд 30
Морис Эшер родился в городе Лёвардене нидерландской провинции
Фрисландия, в семье инженера.
В 1903 году семья переехала
в Арнхем, где мальчик некоторое время учился столярному делу и музыке.С 1912 по 1918 годы Морис учился в средней школе.
Хотя с раннего возраста он проявлял способности к рисованию, его успехи в школе были весьма посредственными.
В 1919 году Эшер поступает в Школу архитектуры и декоративных искусств в городе Гарлеме.
Его учителем там был художник Самуэль де Мескита, оказавший на молодого человека огромное влияние.
В начале 1920-х Эшер часто путешествует в Италию.
Затем Эшер переехал в Шато-д’О (Швейцария).
В январе 1941 года, после начала Второй мировой войны, Эшеры возвращаются в Нидерланды.
С 1940-х по 1970-е они жили в голландском городе Барн (Baarn). В июле 1969 года Эшер создает свою последнюю гравюру на дереве — «Змеи».
Эшер скончался 27 марта 1972 года в своем доме в Ларене, на севере Нидерландов.





























