Слайд 2
Нелинейный уравнения с одной переменной подразделяются на
алгебраические
и трансцидентные
Определение:
Уравнение f(x)=0, называется алгебраическим, если функция f(x)
является алгебраической. (содержит переменную х в различной степени)
Трансцендентное уравнение – уравнение не являющееся алгебраическим. Обычно это уравнение, содержащие показательные, логарифмические, тригонометрические; обратные тригонометрические функции.
Более строгое определение таково:
Трансцендентное уравнение – это равнение вида , где функции f и g являются аналитическим функциями, и по крайне мере одна из них не является алгебраической.
Слайд 3
Определите тип уравнения:
1)
2)
3)
4)
Слайд 4
Если уравнение не решается точными методами, то находим
крни уравнения численными методами:
.
Определение x0 называется корнем уравнения
f(x)=0, если при подстановке x0 в это уравнение получаем верное равенство f(x0)=0.
Приближенный метод решения уравнения состоит из 2-х этапов
1)Отделение корней, т.е определение таких отрезов, в каждом из которых
содержится только один корень.
Используются а) графический метод
б) аналитический метод
2) Уточнение корней, т.е. доведение их до заданной степени точности
Слайд 5
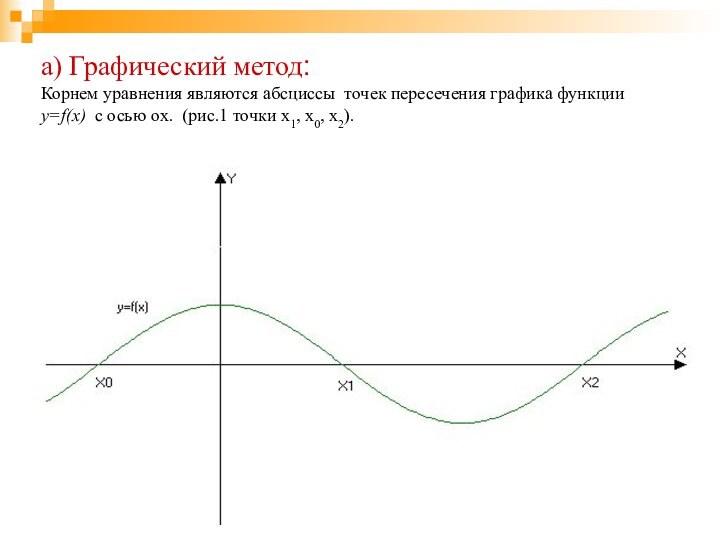
а) Графический метод:
Корнем уравнения являются абсциссы точек
пересечения графика функции
y=f(x) с осью ox. (рис.1 точки
x1, x0, x2).
Слайд 6
Если построение графика функции y=f(x) вызывает затруднение,
то
уравнение y=f(x) нужно представить в виде f1(x)=f2(x), та чтобы
построить графики функций y=f1(x); y= f2(x) было легко.
Корнями уравнения f(x)=0 будут являться абсциссы точек пересечения
графиков функций y=f1(x) и y= f2(x).
Слайд 7
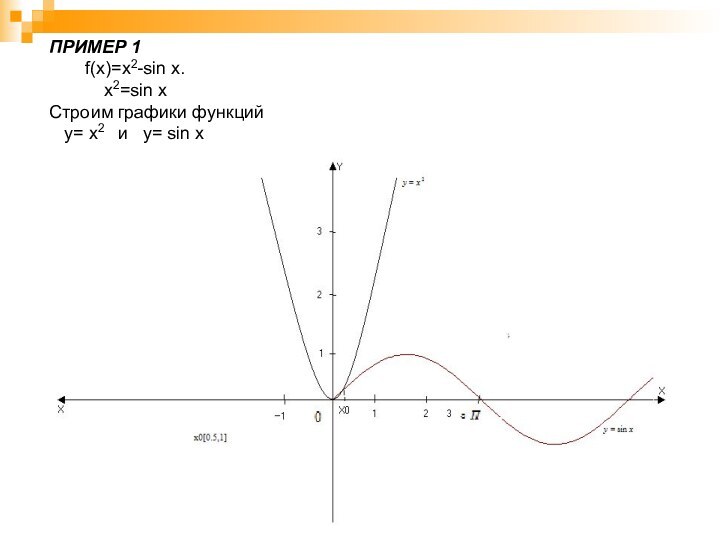
ПРИМЕР 1
f(x)=x2-sin x.
x2=sin x
Cтроим графики функций
y= x2 и
y= sin x
Слайд 8
Отделяющий отрезок [a;b] достаточно малой длинны
следует выбрать так, чтобы
значения f(a) и f(b) были
разных знаков, т.е. f(a)•f(b)<0.
Кроме того точки a, b нужно выбирать так, чтобы значения f(a) и f(b) можно было
легко найти.
Слайд 9
ТЕОРЕМА. Если функция f(x) непрерывна на [
] и на его концах принимает значения
разных знаков, то внутри этого отрезка содержится по крайней мере один корень
При этом используется теорема.
Если f´(x) сохраняет знак на отрезке [a,b] и корень находится внутри отрезка, то он единственный.
Алгоритм отделения корней:
Найти
б) Аналитический метод:
2) Решим уравнение ,Пусть х=a ;х=b. Корни этого уравнения
3)Определим знаки функции f=(а) и f=(b)
-если знаки разны, следовательно на этом интервале есть один корень.
-если знаки одинаковы то корня на интервале нет.
Рассмотрим пример:
Слайд 10
Пример 1 Отделить графически корни уравнения.
Преобразуем данное уравнение к
виду
то есть равенство двух функций :
Корни исходного уравнения графиков
этих абсцисс точек пересечения графиков этих функций.
На одной координатной плоскости построим графики функции
и
Слайд 11
то есть корень принадлежит интервалу [-2;-1]
Слайд 12
ПРИМЕР 2
x5-2x4+x3-1=0
Решение:
Найдем производную исходной функции
1) f´(x)=5x4-8x3+3x2=x2(5x2-8x+3)
Приравняем производную к 0. и
решим уравнение
2) x=0 5x2-8x+3=0
x2(5x2 -8x+3)=0
D=b2-4ac=64-60=4
x1= =0.6 x2=1
x1=0, x2=0.6, x3=1
(-∞;0) (0;0.6) (0.6;1) (1;+∞)
f(x) – монотонна в каждом из этих интервалах.
3) Определили знак функции на концах каждого интервала
(-∞;0) f(-∞)<0; f(0)=-1<0 - т.е. на этом интервале корней нет.
(1;0.6) f(0)<0 f(0.6)<0 – корней нет.
f(1)=-10 – есть корень – один
действительный.
Сузим промежуток. Найдем значения функции при х=2 f(2)>0 то есть корень уравнения лежит в интервале [1;2]
Таким образом корень исходного уравнения x0 (1;2)
Слайд 14
Уточнение корней
Метод простых итераций
Метод Ньютона (касательных)
Метод секущих
Метод
хорд
Комбинированный метод
Метод половинного деления
Слайд 15
Метод простых итераций
Идея метода: корень уравнения - это
такое число, при подстановке которого в уравнение, оно обращается
в верное равенство.
Если переписать исходное уравнение в виде x=g(x), то при подстановке значения корня равенство сохранится.
Такой вид уравнения называется генерирующим соотношением.
Пусть x0 будет исходным приближенным значением корня уравнения x=g(x). Тогда в качестве следующего приближения примем: x1=g(x0), второе приближение получим, подставив в правую часть уравнения первое приближение: x2=g(x1) и т.д. В общем виде: xn=g(xn-1).
Процесс получения последовательных приближений значения корня называется итерационным, а метод – методом простых итераций.
Для определения достижения точности пользуются неравенством или .
Слайд 16
Пример1
1) 2x + lg(2x + 3)=l;
Найдем приближенные
значения корней графически; для этого уравнение удобно представить в
виде lg(2x + 3) = 1 -2х (рис.4). Из графика видно, что уравнение имеет один корень, лежащий в промежутке [0; 0,5]. Для уточнения его методом итераций приведем уравнений к виду х = φ(х).
Функцию φ (х) будем искать из соотношения считая, что ,где ;число k имеет тот же знак, что и в промежутке [0; 0,5].
Находим
f(x )=2х + lg (2х + 3) — 1;
при
Слайд 17
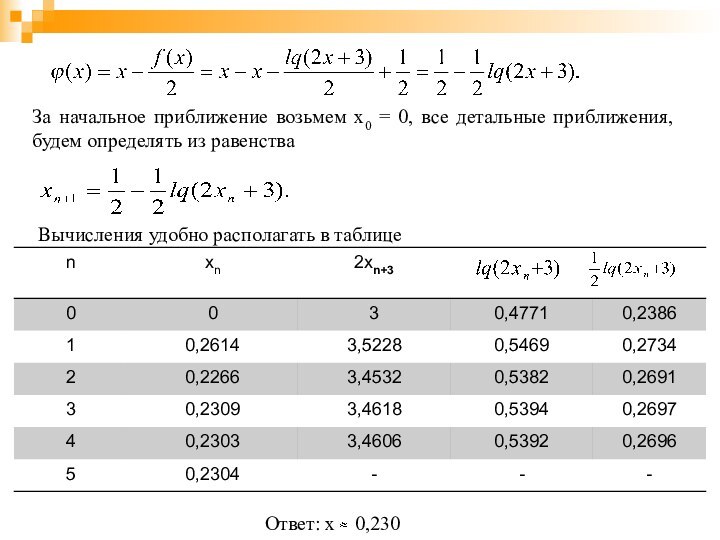
За начальное приближение возьмем x0 = 0, все
детальные приближения, будем определять из равенства
Вычисления удобно располагать в
таблице
Ответ: х 0,230
Слайд 18
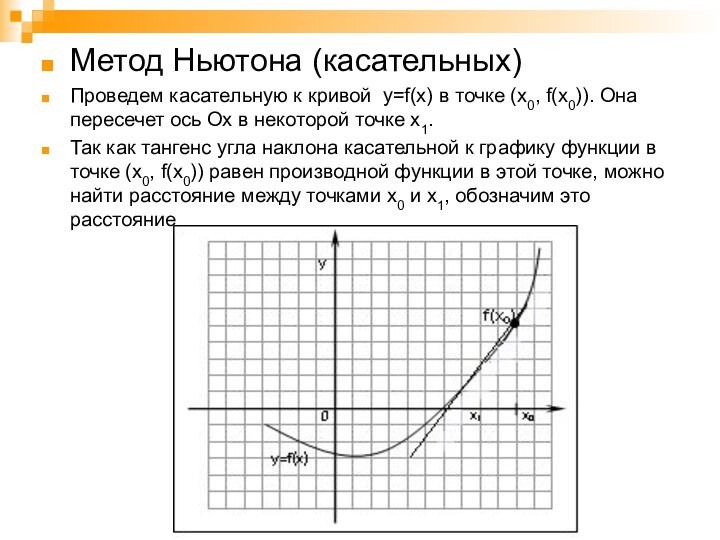
Метод Ньютона (касательных)
Проведем касательную к кривой y=f(x) в
точке (x0, f(x0)). Она пересечет ось Ох в некоторой
точке х1.
Так как тангенс угла наклона касательной к графику функции в точке (x0, f(x0)) равен производной функции в этой точке, можно найти расстояние между точками х0 и х1, обозначим это расстояние
Слайд 19
Тогда координату точки х1 можно определить следующим образом:
Аналогично
можно найти точки х2, х3, …, хn, …
Таким образом,
для расчета приближений в методе Ньютона используется формула:
Счет прекращается при достижении достаточного малого значения .
Это самый быстрый метод. Скорость сходимости в большей мере зависит от удачного выбора исходной точки.
Если в процессе вычислений на каком-то шаге тангенс угла наклонной касательной обращается в нуль, т.е. f`(x)=0, то применение метода усложняется.
Слайд 20
Сходимость метода обеспечивается при следующих условиях:
x0 выбрано
достаточно близко к корню уравнения f(x)=0;
Вторая производная
не становится очень большой;
Первая производная не слишком близко к нулю. Последнее условие означает, что никакие два корня не находятся слишком близко один к другому.
Пример1
1) tg(0,55x+0,l) = x2;
Выше мы установили, что уравнение имеет действительный корень, принадлежащий промежутку [-1,0]. Уточним этот корень методом касательных. Так как и ,то за начальное приближение принимаем x0=-1.
Для вычисления применяем формулу
Слайд 21
Находим
Для вычислений используем таблицу:
Ответ:
.
Слайд 22
Метод секущих
недостатком метода Ньютона состоит в том, что
приходится дифференцировать функцию f(x). Заменим производную, используемую в методе
Ньютона, отношением разностей:
Тогда формула примет вид:
Слайд 23
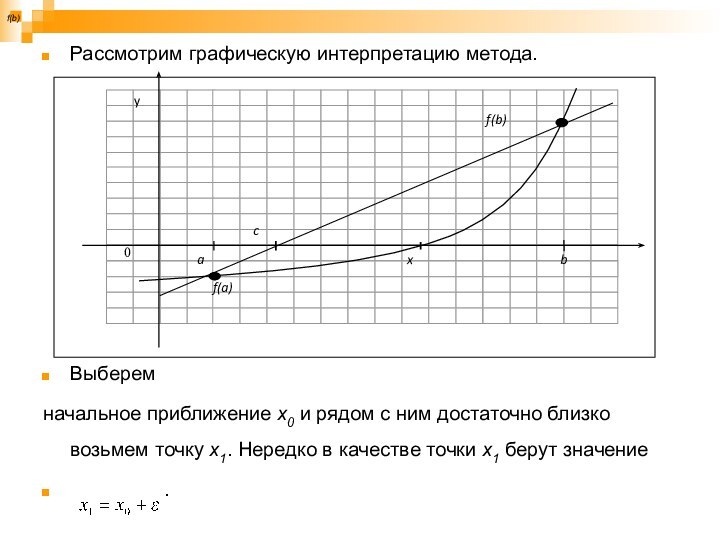
Рассмотрим графическую интерпретацию метода.
Выберем
начальное приближение х0 и
рядом с ним достаточно близко возьмем точку х1. Нередко
в качестве точки х1 берут значение
.
f(b)
Слайд 24
Через точки f(х0) и f(х1) проведем прямую –
секущую. Она пересекает ось Oх в некоторой точке х2.
Вычислим координаты этой точки. Для этого воспользуемся уравнением прямой, проходящей через две точки:
Т.к. искомая точка лежит на оси Oх, то ордината этой точки, т.е. y равна нулю. Следовательно, получим следующую формулу:
это и есть формула метода секущих.
f(b)
Слайд 25
Последующие приближения будем получать, используя эту же формулу
до тех пор, пока не будет достигнута требуемая точность,
т.е. .
Метод секущих, так же, как и метод касательных, сходится не всегда. Причины сходимости – те же, что и у метода касательных.
Слайд 26
Метод хорд
Метод хорд легко получается из метода секущих.
Если в качестве начальных приближений выбрать не две рядом
лежащие точки, а концы отрезка, содержащего искомый корень (мы его получили на этапе отделения корней), можно избежать существенного недостатка предыдущих методов – возможную расходимость метода. Метод хорд сходится всегда. Но алгоритм метода становится сложнее. Рассмотрим геометрическую интерпретацию метода.
Слайд 27
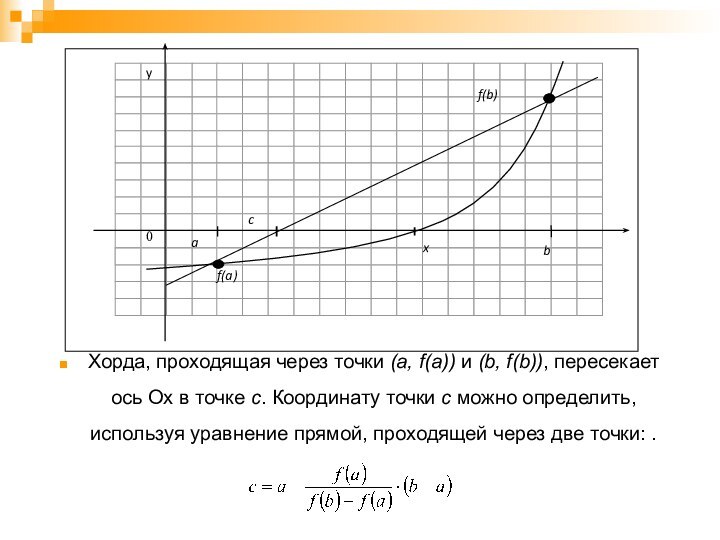
Хорда, проходящая через точки (a, f(a)) и (b,
f(b)), пересекает ось Ох в точке с. Координату точки
с можно определить, используя уравнение прямой, проходящей через две точки: .
Слайд 28
Формула метода хорд такая же, как и в
методе секущих. Но, в отличие от метода секущих, где
все получаемые приближения лежат по одну сторону от корня, в методе хорд получаемое приближение всегда лежит между двумя предыдущими! Следовательно, необходимо проверять на каком отрезке - [a, c] или [c, b] лежит искомый корень. Для этого достаточно проверить произведение значений функции на концах получившихся отрезков (см. отделение корней): корень есть, если данное произведение меньше нуля.
Далее выбираем тот из отрезков, на котором содержится корень. В нашем случае – это отрезок [c, b].
Слайд 29
Переименуем один из концов отрезка так, чтобы опять
получился отрезок [a, b]. Найдем новое значение с и
буде повторять процесс до тех пор, пока не будет достигнута требуемая точность.
Слайд 30
Пример 1
Находим:
Составим таблицу знаков функции f(x):
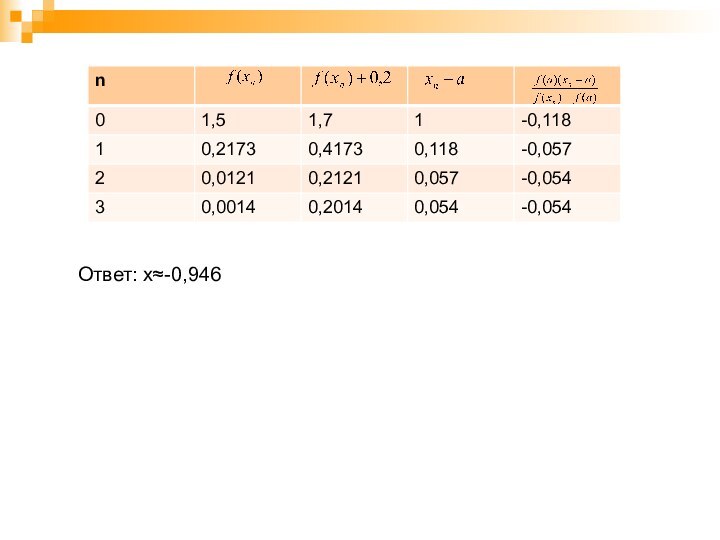
Слайд 31
Уравнение имеет один действительный корень, лежащий в промежутке
[-1,0].
Чтобы уточнить корень, находим вторую производную
в промежутке [-1,0] выполняется
неравенство
Для вычисления применяем формулу
где
Вычисление располагаем в таблице:
Слайд 33
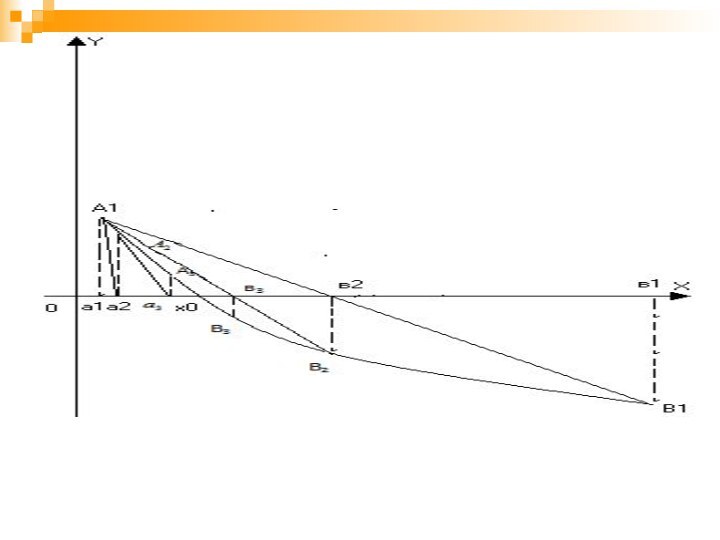
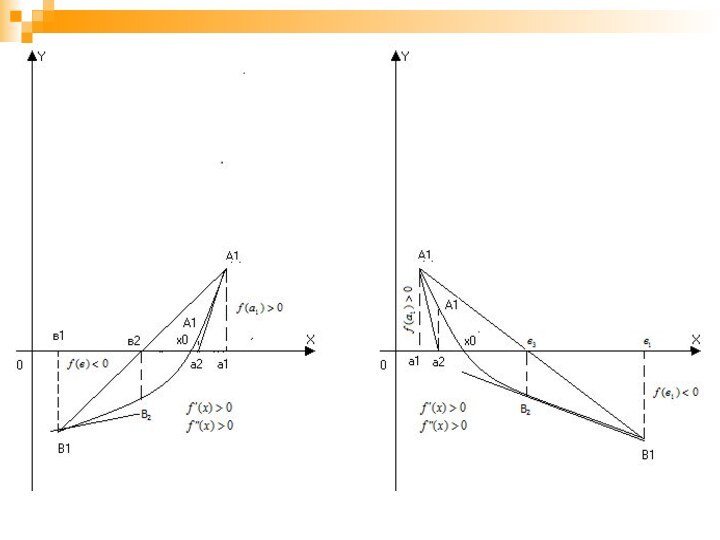
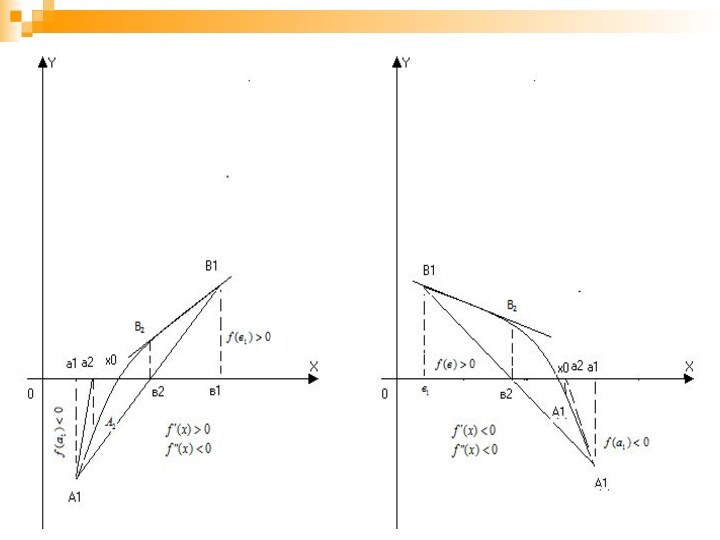
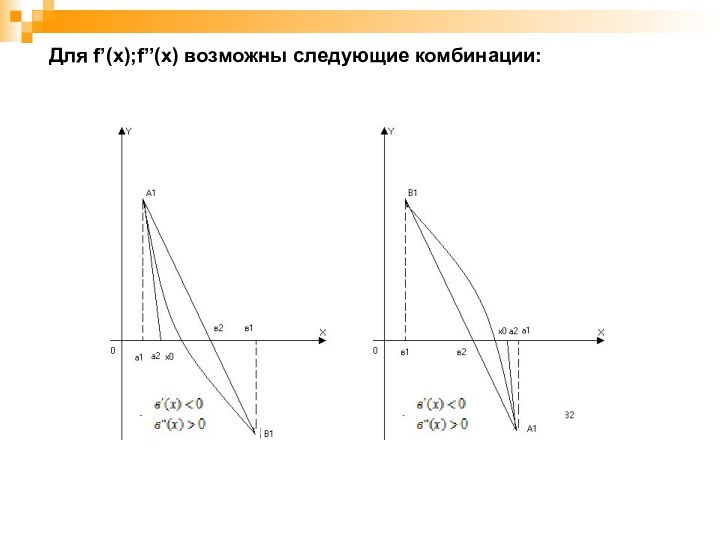
Для f’(x);f’’(x) возможны следующие комбинации:
Слайд 34
Замечание: условимся через a1 обозначать тот конец отрезка
[a1,b1] где
совпадают знаки f’(x) и f’’(x).
Слайд 35
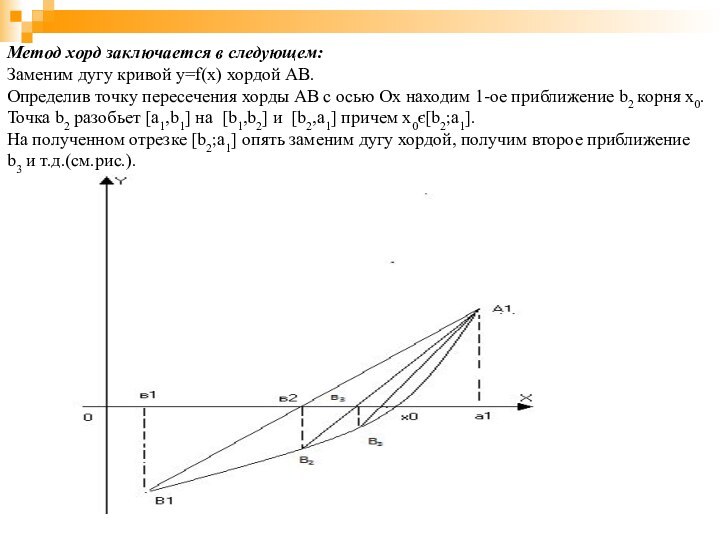
Метод хорд заключается в следующем:
Заменим дугу кривой y=f(x)
хордой AB.
Определив точку пересечения хорды AB с осью Ox
находим 1-ое приближение b2 корня x0.
Точка b2 разобьет [a1,b1] на [b1,b2] и [b2,a1] причем x0є[b2;a1].
На полученном отрезке [b2;a1] опять заменим дугу хордой, получим второе приближение
b3 и т.д.(см.рис.).
Слайд 36
Выведем формулу для n-го приближения.
Уравнение прямой, проходящей через
две точки A(a1;f(a1)) и Bn(вn;f(вn))
имеет вид:
Найдем точку
пересечения этой прямой с осью абсцисс, полагая y=0, x=bn+1
имеем
n=1;2;3.
Слайд 37
Метод касательных отличается от метода хорд тем, что
дугу
заменяют не хордой, а касательной.
В точке
проведем касательную к дуге. Точка
пересечения касательной и оси Ох – будет первым
приближением корня
Затем проведем касательную в точке и получим
второе приближенное значение и т.д.
Слайд 38
Выведем формулу для n –го приближения:
Уравнение касательной
в точке
будет иметь вид:
где n=1,2,3…
Пологая, что и , имеем
(2)
где n=1,2,3…
Процесс сходится, если и , непрерывна и
сохраняет свои знаки на
Слайд 39
Комбинированный метод
Суть приближения по методу хорд будет располагаться
с одной
стороны, а по методу касательных - с другой
т.е. в результате мы
придем к следующему
где найдено по формуле
(3)
Слайд 41
Последний из полученных интервалов дает абсолютную величину
погрешности приближенного
значения корня.
Пусть
, где - заданная точность
приближенного значения корня за приближенное значение
можно взять в частности .
Погрешность этого приближения
Замечание
За берем ту точку где и имеют одинаковые знаки.
Слайд 44
Пример 1
определено что
1. Уточним
значение корня: делим отрезок [1;2] пополам – [1;1,5] и
[1,5;2], то
2. Исследование:
а)
б)
Слайд 47
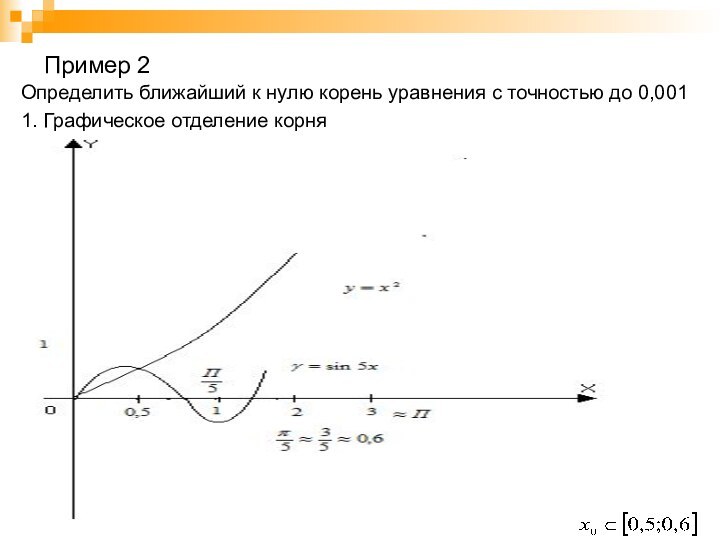
Пример 2
Определить ближайший к нулю корень уравнения с
точностью до 0,001
1. Графическое отделение корня
Слайд 48
2. Исследование
а)
б)
в)
т.е. случай 1
Применяем формулу (3)
Слайд 49
Метод половинного деления
Метод хорд можно сделать проще. Так
как точка с – это точка лежащая между a
и b, ее координаты можно определить иначе – поделить отрезок [a, b] пополам: . Если f(x)≠0 (что наиболее вероятно), то возможны два случая: либо f(x) меняет знак на отрезке [a,c], либо на отрезке [c,b]. Выбирая в каждом случае тот из отрезков, на котором происходит смена знака функции, и, продолжая метод половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения. Т.е., процесс будем продолжать до тех пор, пока не будет достигнута требуемая
точность:
Слайд 50
Пример метода половинного деления
Умножить корни уравнения
Методом половинного
деления:
Ранее было установлено, что корень уравнения принадлежит
разобьем его
На два интервала и
И определяем знаки исходной функции на концах интервала:
на промежутке -есть корень.
-нет корней.
Промежуток
поделим пополам и
-нет корней.
-есть корень.
Вновь разобьем интервал пополам.
и
-есть корень.
-нет корня.
Середину отрезка
Возьмем за корень: 1,6875.





![Презентация по вычислительной математике на тему Приближенные методы решения уравнений Отделяющий отрезок [a;b] достаточно малой длинны следует выбрать так, чтобы](/img/tmb/6/579000/b3b73bcfad1b1ccf665c8aa594341e28-720x.jpg)
![Презентация по вычислительной математике на тему Приближенные методы решения уравнений ТЕОРЕМА. Если функция f(x) непрерывна на [ ] и](/img/tmb/6/579000/6702fec14fa377983d63d24800eb99d8-720x.jpg)

![Презентация по вычислительной математике на тему Приближенные методы решения уравнений то есть корень принадлежит интервалу [-2;-1]](/img/tmb/6/579000/4549a24228ebd3ed27d15156fd46473d-720x.jpg)













![Презентация по вычислительной математике на тему Приближенные методы решения уравнений Переименуем один из концов отрезка так, чтобы опять получился отрезок [a, b].](/img/tmb/6/579000/4463b6f757cd4fd8397702c37fb7b247-720x.jpg)

![Презентация по вычислительной математике на тему Приближенные методы решения уравнений Уравнение имеет один действительный корень, лежащий в промежутке [-1,0].Чтобы уточнить корень, находим](/img/tmb/6/579000/801f7cb592261d15e1e3401e29e011f3-720x.jpg)
![Презентация по вычислительной математике на тему Приближенные методы решения уравнений Замечание: условимся через a1 обозначать тот конец отрезка [a1,b1] где](/img/tmb/6/579000/1654c707844314531fce96a7faf097b8-720x.jpg)