по формуле Ньютона-Лейбница, используя знания о первообразной и правила
её вычисленияЗадачи занятия:
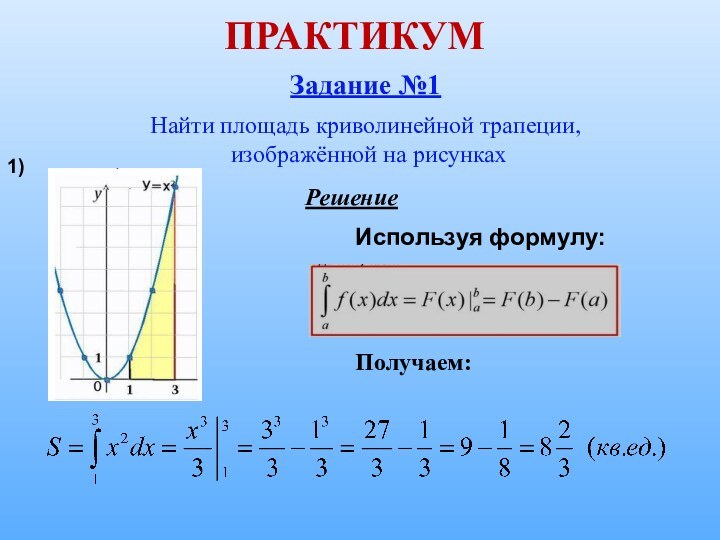
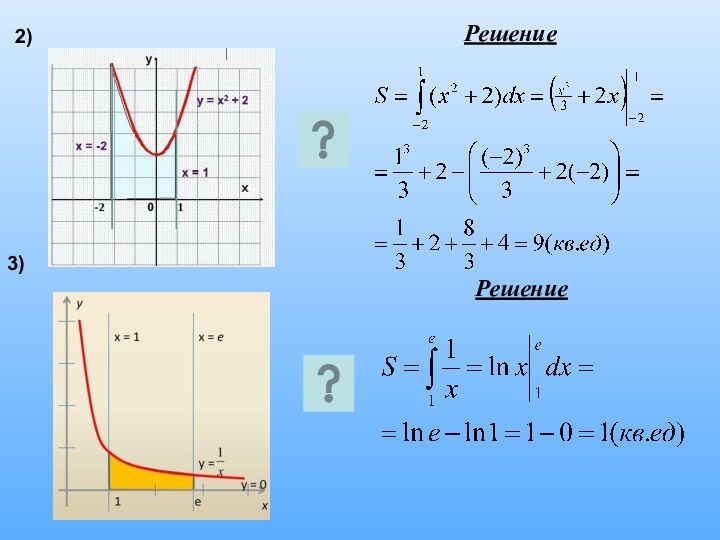
1. Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции.
2. Обобщить и систематизировать знания, проверить усвоение изученного материала
3. Закрепить изученное в ходе выполнения упражнений.
Задачи занятия:
1. Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции.
2. Обобщить и систематизировать знания, проверить усвоение изученного материала
3. Закрепить изученное в ходе выполнения упражнений.
Задачи занятия:
1. Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции.
2. Обобщить и систематизировать знания, проверить усвоение изученного материала
3. Закрепить изученное в ходе выполнения упражнений.
Задачи занятия:
1. Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции.
2. Обобщить и систематизировать знания, проверить усвоение изученного материала
3. Закрепить изученное в ходе выполнения упражнений.
Задачи занятия:
1. Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции.
2. Обобщить и систематизировать знания, проверить усвоение изученного материала
3. Закрепить изученное в ходе выполнения упражнений.








![Презентация по математике на тему Определённый интеграл. Вычисление площади криволинейной трапеции Понятие о криволинейной трапеции. Определённый интегралФигура, ограниченная неотрицательной на отрезке [a;b] функцией](/img/tmb/6/587657/e27cfc1819f2c5fb6b5d37f18a7c866a-720x.jpg)


![Презентация по математике на тему Определённый интеграл. Вычисление площади криволинейной трапеции Геометрический смысл интегралаОпределённый интеграл от неотрицательной непрерывной функции f(x) по [a, b] численно равен площади криволинейной трапеции с основанием [a, b],](/img/tmb/6/587657/8821f2923acf0af4886bb1843c085948-720x.jpg)