Слайд 2
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Рисунок 20
vk
v1
v
v2
T1
Tk
T2
Слайд 3
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Вершины v1, ..., vk
графа Т − это сыновья корня v (рис. 20).
Мы изображаем такое дерево с корнем, расположенным наверху, и сыновьями, стоящими ниже, непосредственно под корнем.
Вершина на самом верху дерева − его корень (v), а вот те, которые находятся в самом низу дерева (и не имеют сыновей) принято называть листьями. Остальные вершины, отличные от корня и листьев, называют внутренними.
Двоичные или бинарные деревья с корнем. Двоичное дерево отличает от остальных то, что каждая его вершина имеет не более двух сыновей. В двоичном дереве с корнем вниз от каждой вершины идет не более двух ребер.
Слайд 4
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Каждой вершине двоичного дерева
с корнем соответствует не более, чем два поддерева, которые
принято называть левым и правым поддеревьями этой вершины.
Если оказалось, что у какой-то вершины дерева отсутствует потомок слева, то ее левое поддерево называют нулевым деревом (т.е. нулевое дерево − это дерево без единой вершины). Аналогично, если у вершины отсутствует правый потомок, то ее правое поддерево будет нулевым.
Слайд 5
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
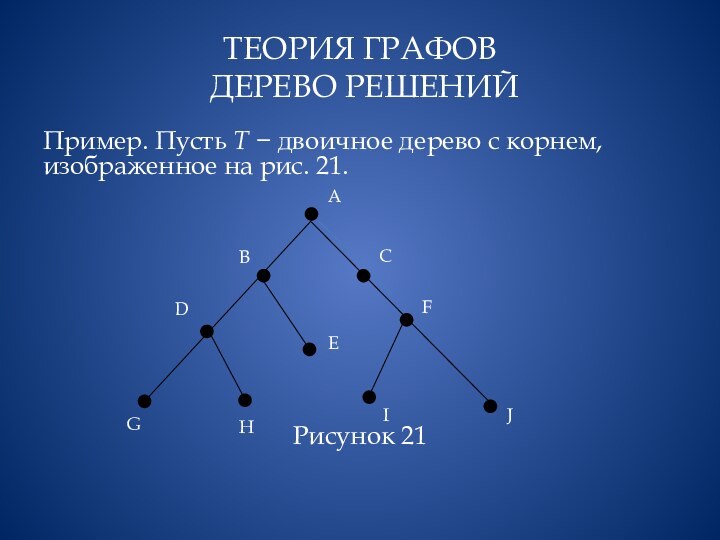
Пример. Пусть Т −
двоичное дерево с корнем, изображенное на рис. 21.
Рисунок 21
A
B
C
D
E
G
H
I
J
F
Слайд 6
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Определите
а) корень Т;
б) корень
левого поддерева вершины B;
в) листья Т;
г) сыновей вершины С.
Нарисуйте
двоичное дерево с корнем Т’, полученное из Т перестановкой левых и правых поддеревьев у каждой вершины.
Слайд 7
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
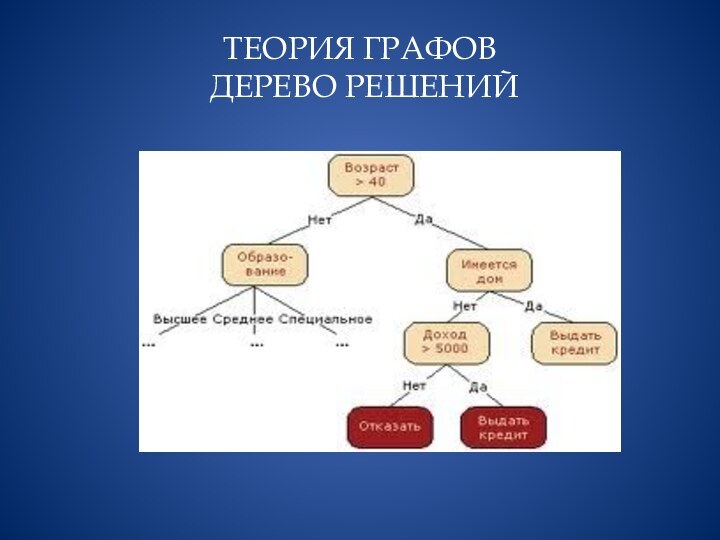
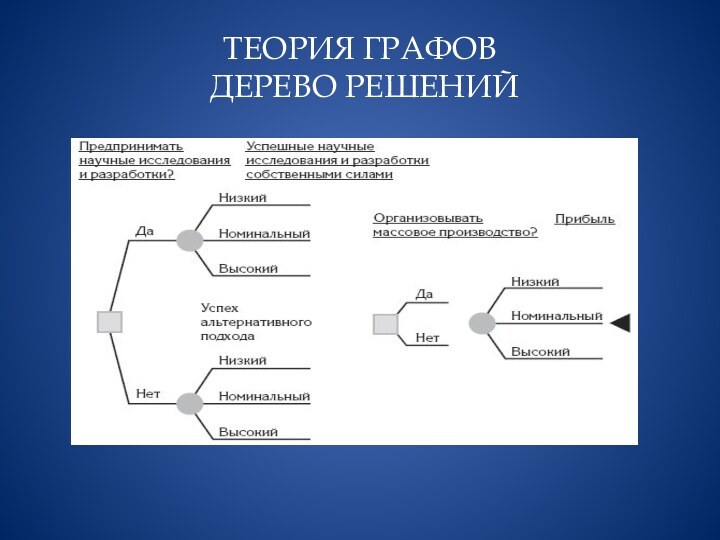
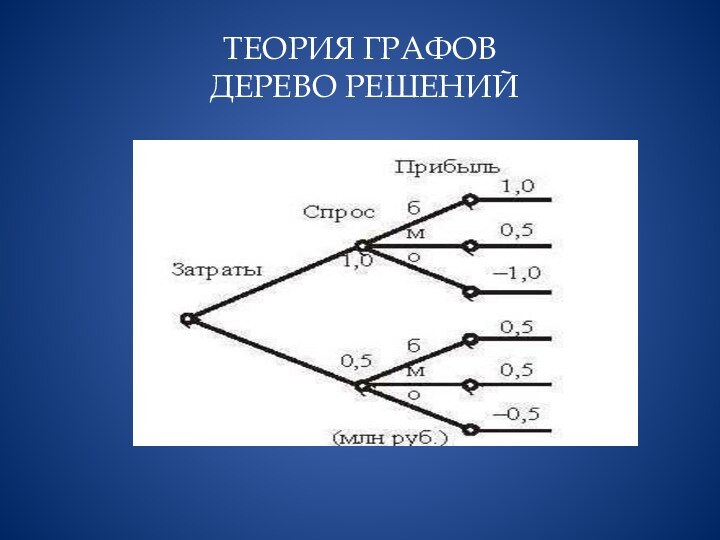
Дерево решений − используется
в области анализа данных для прогнозных моделей. Структура дерева
представляет собой следующее: «листья» и «ветки». На ребрах («ветках») дерева решения записаны атрибуты, от которых зависит целевая функция, в «листьях» записаны значения целевой функции, а в остальных узлах − атрибуты, по которым различаются случаи. Чтобы классифицировать новый случай, надо спуститься по дереву до листа и выдать соответствующее значение. Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной на основе нескольких переменных на входе.
Слайд 8
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Слайд 9
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Слайд 11
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Метод поиска с деревом
решений состоит в разбиении начальной задачи Р0 на некоторое
число подзадач Р1, Р2,…,Рk (в целом представляющих всю задачу Р0) с последующей попыткой разрешить каждую из этих подзадач.
Слайд 12
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Выражение разрешить понимаем так:
найти
оптимальное решение;
показать, что значение оптимального решения хуже, чем для
полученного до этого наилучшего решения;
показать, что подзадача не является допустимой.
Слайд 13
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
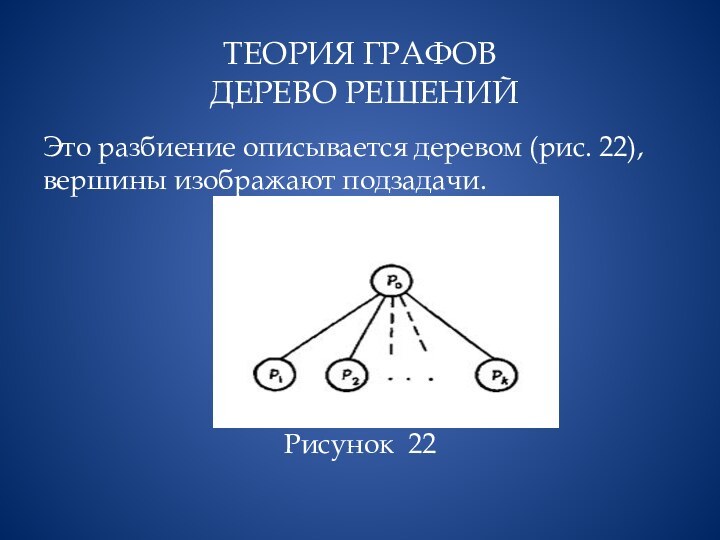
Это разбиение описывается деревом (рис.
22), вершины изображают подзадачи.
Рисунок 22
Слайд 14
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
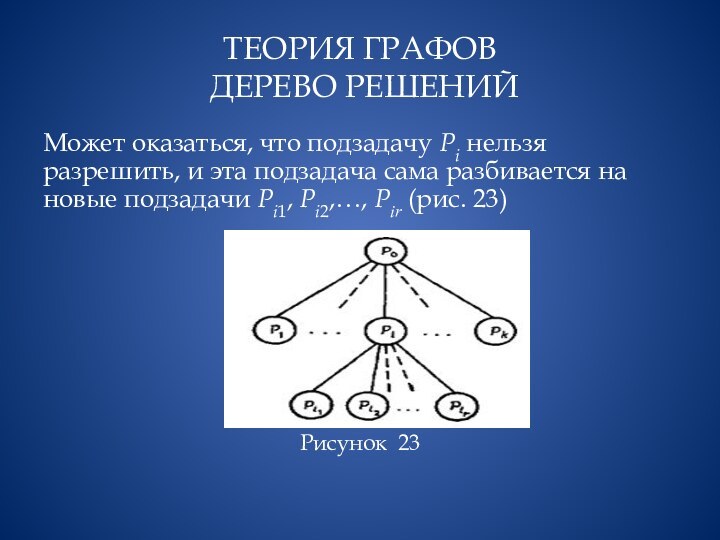
Может оказаться, что подзадачу Рi
нельзя разрешить, и эта подзадача сама разбивается на новые
подзадачи Рi1, Рi2,…, Рir (рис. 23)
Рисунок 23
Слайд 15
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Это разбиение, называемое ветвлением, повторяется
для каждой подзадачи, которая не может быть разрешена.
На любом
этапе полное множество подзадач, требующих разрешения, представляется множеством концевых вершин (т.е. вершин степени 1) всех цепей, выходящих из корня дерева решений. Эти вершины называются висячими, и на рис. 23 это Р1,…, Рi-1, Рi1,…, Рir, Рi+1,…,Рk
Слайд 16
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Если поиск исчерпан, то очевидно,
что множество подзадач, на которые разбита задача, должно представлять
всю задачу. Таким образом, если задача Рi разбита на r подзадач Рi1, …, Рir, то
{Рi1}∪{Рi2} ∪… ∪{Рir}={Рi},
где {Р} обозначает множество всех допустимых решений задачи Р.
Слайд 17
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Любая подзадача, представляемая висячей вершиной
и не поддающаяся разрешению, может быть в любой момент
разбита на меньшие подзадачи. Существует два основных типа поиска в зависимости от того, как выбирается следующая висячая вершина для продолжения процесса ветвления.
Слайд 18
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Поиск в ширину (рис. 24)
При поиске
по ширине ветвление происходит от уровня к уровню, так,
что если на уровне 1 начальная задача Р0 разбивается на подзадачи Р1,Р2,…,Рk, то каждая их этих подзадач исследуется раньше, чем задачи уровня 2. Задачи уровня 1, которые не могут быть разрешены, разбиваются на подзадачи уровня 2, и опять все они исследуются до исследования какой-либо подзадачи, могущей возникнуть на уровне 3 и т.д.
Слайд 19
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Рисунок 24
Слайд 20
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Т.е. на каждой следующей итерации своей
работы он расползается вширь по ребрам от вершин, до
которых он дошёл к данной итерации. И так расползается он до тех пор, пока не побывает в каждой вершине текущей компоненты связности.
Чаще всего поиск в ширину используется для нахождения кратчайшего пути от одной вершины до другой
Слайд 21
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Поиск в глубину (рис. 25)
Этот алгоритм
делает следующее:
поиск в глубину от начальной вершины не
расползается вширь, а уходит в вглубь по смежным рёбрам. Если из текущей вершины он не может дальше идти вглубь (все смежные вершины помечены) , то он откатывается на предыдущую вершину (из которой он попал в текущую) и продолжает просматривать смежные вершины оттуда.
Слайд 22
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Рисунок 25
Слайд 23
ТЕОРИЯ ГРАФОВ
ДЕРЕВО РЕШЕНИЙ
Применение границ
Если задача Р0 подлежит решению
как задача оптимизации, то безотносительно к типу поиска этот
поиск завершается только тогда, когда будут разрешены все подзадачи, представляемые висячими вершинами. Для ускорения процесса разрешения для каждой из висячих вершин вычисляется нижние или верхние границы (для случаев минимизации или максимизации соответственно).