Слайд 2
Число́ — основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей.
Письменными знаками для обозначения чисел служат цифры, а также символы математических операций. Возникнув
ещё в первобытном обществе из потребностей счёта, понятие числа с развитием науки значительно расширилось.
Слайд 3
Виды чисел
История развития арифметики.
Представление чисел в памяти компьютера.
Основные
числовые множества.
Иерархия чисел.
Слайд 4
1. История развития арифметики
«Число» в истории
Доисторические времена.
Появление письменности
Появление
арифметики
Введение отрицательных чисел
Введение действительных чисел
Введение комплексных чисел
Слайд 5
1.1.«Число» в истории.
Понятие числа возникло в глубокой древности из
практической потребности людей и усложнялось в процессе развития человечества.
Область человеческой деятельности расширялась и соответственно, возрастала потребность в количественном описании и исследовании. Сначала понятие числа определялось теми потребностями счёта и измерения, которые возникали в практической деятельности человека, всё более усложняясь. Позже число становится основным понятием математики, и потребности этой науки определяют дальнейшее развитие этого понятия.
Слайд 6
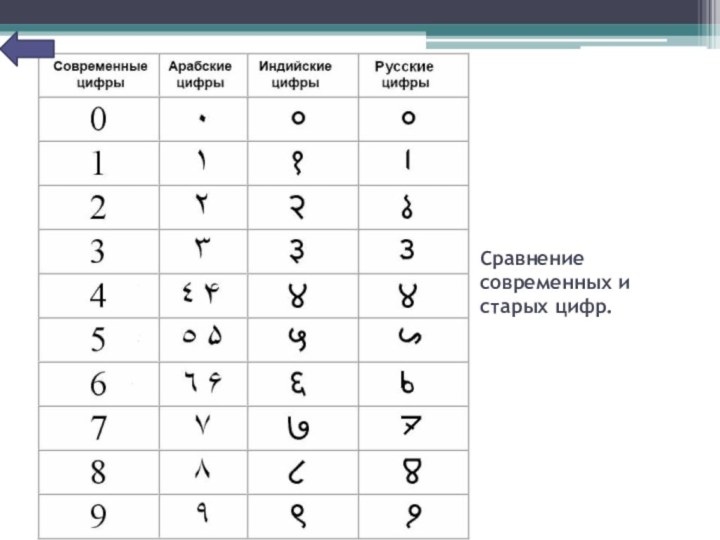
Сравнение современных и старых цифр.
Слайд 7
1.2. Доисторические времена.
Считать предметы человек умел ещё в
глубокой древности, тогда и возникло понятие натурального числа. На
первых ступенях развития понятие отвлечённого числа отсутствовало. В те времена человек мог оценивать количества однородных предметов, называемых одним словом, например "три человека", "три топора". При этом использовались разные слова "один" "два", "три" для понятий "один человек", "два человека", "три человека" и "один топор", "два топора", "три топора". Это показывает анализ языков первобытных народностей.
Слайд 8
Такие именованные числовые ряды были очень короткими и
завершались неиндивидуализированным понятием "много". Разные слова для большого количества предметов
разного рода существуют и сейчас, такие, как "толпа", "стадо", "куча". Примитивный счёт предметов заключался «в сопоставлении предметов данной конкретной совокупности с предметами некоторой определённой совокупности, играющей как бы роль эталона», которым у большинства народов являлись пальцы ("счёт на пальцах"). Это подтверждается лингвистическим анализом названий первых чисел. На этой ступени понятие числа становится не зависящим от качества считаемых объектов.
Слайд 9
1.3. Появление письменности
Возможности воспроизведения чисел значительно увеличились с
появлением письменности. Первое время числа обозначались чёрточками на материале, служащем
для записи, например папирус, глиняные таблички, позже стали применяться специальные знаки для некоторых чисел (сохранившиеся до наших дней "римские цифры") и знаки для больших чисел. О последних свидетельствуют вавилонские клинописные обозначения или знаки для записи чисел в кириллической системе счисления. Когда в Индии появилась позиционная система счисления, позволяющая записать любое натуральное число при помощи десяти знаков (цифр), это стало большим достижением человека.
Слайд 10
Осознание бесконечности натурального ряда явилось следующим важным шагом в развитии
понятия натурального числа. Об этом есть упоминания в трудах Евклида и
Архимеда и других памятниках античной математики 3 века до н. э. В "Началах" Евклид устанавливает безграничную продолжаемость ряда простых чисел. Здесь же Евклид определяет число, как “множество, составленное из единиц”. Архимед в книге "Псаммит" описывает принципы для обозначения сколь угодно больших чисел.
Слайд 11
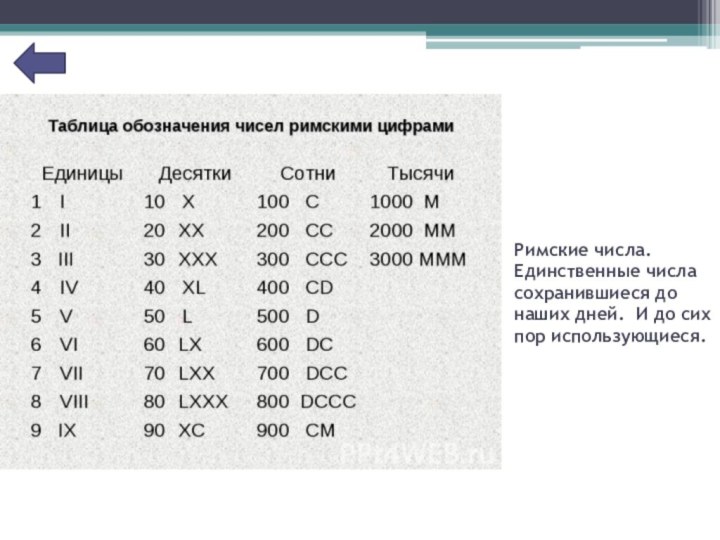
Римские числа. Единственные числа сохранившиеся до наших дней.
И до сих пор использующиеся.
Слайд 12
1.4. Появление арифметики.
Со временем начинают применяться действия над
числами, сначала сложение и вычитание, позже умножение и деление. В результате длительного развития сложилось представление
об отвлечённом характере этих действий, о независимости количественного результата действия от рассматриваемых предметов, о том, что, например, два предмета и три предмета составляют пять предметов независимо от характера этих предметов. Когда стали разрабатывать правила действий, изучать их свойства и создавать методы решения задач, тогда начинает развиться арифметика — наука о числах.
Слайд 13
Потребность в изучении свойств чисел как таковых проявляется
в самом процессе развития арифметики, становятся понятными сложные закономерности и
их взаимосвязи, обусловленные наличием действий, выделяются классы чётных и нечётных чисел, простых и составных чисел и так далее. Тогда появляется раздел математики, который сейчас называется теория чисел. Когда было замечено, что натуральные числа могут характеризовать не только количество предметов, но и ещё могут характеризовать порядок предметов, расположенных в ряд, возникает понятие порядкового числа. Вопрос об обосновании понятия натурального числа, столь привычного и простого, долгое время в науке не ставился.
Слайд 14
Только к середине 19 века под влиянием развития математического
анализа и аксиоматического метода в математике, назрела необходимость обоснования понятия количественного
натурального числа. Введение в употребление дробных чисел было вызвано потребностью производить измерения и стало исторически первым расширением понятия числа.
Слайд 15
1.5. Введение отрицательных чисел
В Средние века были введены отрицательные числа, с
помощью которых стало легче учитывать долг или убыток. Необходимость
введения отрицательных чисел была связана с развитием алгебры как науки, дающей общие способы решения арифметических задач, независимо от их конкретного содержания и исходных числовых данных. Необходимость введения в алгебру отрицательного числа возникает уже при решении задач, сводящихся к линейным уравнениям с одним неизвестным. Отрицательные числа систематически применялись при решении задач ещё в 6—11 веках в Индии и истолковывались примерно так же, как это делается в настоящее время.
Слайд 16
После того, как Декарт разработал аналитическую геометрию, позволившую рассматривать корни уравнения как координаты точек пересечения
некоторой кривой с осью абсцисс, что окончательно стёрло принципиальное
различие между положительными и отрицательными корнями уравнения, отрицательные числа окончательно вошли в употребление в европейской науке.
Слайд 17
1.6. Введение действительных чисел.
Ещё в Древней Греции в геометрии было совершено принципиально
важное открытие: не всякие точно заданные отрезки соизмеримы, другими
словами, не у каждого отрезка длина может быть выражена рациональным числом, например сторона квадрата и его диагональ. В "Началах" Евклида была изложена теория отношений отрезков, учитывающая возможность их несоизмеримости. В Древней Греции умели сравнивать такие отношения по величине, производить над ними арифметические действия в геометрической форме. Хотя греки обращались с такими отношениями, как с числами, они не осознали, что отношение длин несоизмеримых отрезков может рассматриваться как число.
Слайд 18
Это было сделано в период зарождения современной математики
в 17 веке при разработке методов изучения непрерывных процессов
и методов приближённых вычислений. И. Ньютон во "Всеобщей арифметике" даёт определение понятия действительного числа: "Под числом мы понимаем не столько множество единиц, сколько отвлечённое отношение какой-нибудь величины к другой величине того же рода, принятой нами за единицу". Позже, в 70 годах 19 века, понятие действительного числа было уточнено на основе анализа понятия непрерывности Р. Дедекиндом, Г. Кантором и К. Вейерштрассом.
Слайд 19
1.7. Введение комплексных чисел.
С развитием алгебры возникла
необходимость введения комплексных чисел, хотя недоверие к закономерности пользования
ими долго сохранялось и отразилось в сохранившемся до сих пор термине "мнимое". Уже у итальянских математиков 16 века (Дж. Кардано, Р. Бомбелли), в связи с открытием алгебраического решения уравнений третьей и четвёртой степеней, возникла идея комплексного числа. Дело в том, что даже решение квадратного уравнения, в том случае, если уравнение не имеет действительных корней, приводит к действию извлечения квадратного корня из отрицательного числа.
Слайд 20
Казалось, что задача, приводящаяся к решению такого квадратного
уравнения, не имеет решения. С открытием алгебраического решения уравнений
третьей степени обнаружилось, что в том случае, когда все три корня уравнения являются действительными, по ходу вычисления оказывается необходимо выполнить действие извлечения квадратного корня из отрицательных чисел.
Слайд 21
После установления в конце XVIII века геометрического истолкования
комплексных чисел в виде точек на плоскости и установления
несомненной пользы от введения комплексных чисел в теории алгебраических уравнений, в особенности после знаменитых работ Л. Эйлера и К. Гаусса, комплексные числа были признаны математиками и начали играть существенную роль не только в алгебре, но и в математическом анализе. Значение комплексных чисел особенно возросло в 19 веке в связи с развитиемтеории функций комплексного переменного.[3]
Слайд 22
2. Представление чисел в памяти компьютера.
Слайд 23
Для представления натурального числа в памяти компьютера, оно обычно
переводится в двоичную систему счисления. Для представления отрицательных чисел часто
используется дополнительный код числа, который получается путём прибавления единицы к инвертированному представлению модуля данного отрицательного числа в двоичной системе счисления.
Представление чисел в памяти компьютера имеет ограничения, связанные с ограниченностью объёма памяти, выделяемого под числа. Даже натуральные числа представляют собой математическую идеализацию, ряд натуральных чисел бесконечен. На объём же памяти ЭВМ накладываются физические ограничения.
Слайд 24
В связи с этим в ЭВМ мы имеем
дело не с числами в математическом смысле, а с
некоторыми их представлениями, или приближениями. Для представления чисел отводится некоторое определенное число ячеек (обычно двоичных, бит — от BInary digiT) памяти. В случае, если в результате выполнения операции полученное число должно занять больше разрядов, чем отводится в ЭВМ, результат вычислений становится неверным — происходит так называемое арифметическое переполнение. Действительные числа обычно представляются в виде чисел с плавающей запятой. При этом лишь некоторые из действительных чисел могут быть представлены в памяти компьютера точным значением, в то время как остальные числа представляются приближёнными значениями.
Слайд 25
В наиболее распространённом формате число с плавающей запятой представляется в
виде последовательности битов, часть из которых кодирует собой мантиссу числа, другая
часть — показатель степени, и ещё один бит используется для указания знака числа.
Слайд 27
3. Основные числовые множества.
Натуральные числа.
Целые числа
Рациональные числа
Действительные (вещественные)
числа
Комплексные числа
Слайд 28
3.1. Натуральные числа.
Натуральные числа, получаемые при естественном
счёте; множество натуральных чисел обозначается N. То есть N={1,2,3,4…} (иногда к множеству натуральных чисел также
относят ноль, то есть N= {0,1,2,3,4…} Натуральные числа замкнуты относительно сложения и умножения (но не вычитания или деления). Сложение и умножение натуральных чисел коммутативны и ассоциативны, а умножение натуральных чисел дистрибутивно относительно сложения и вычитания.
Слайд 29
Важным подмножеством натуральных чисел являются простые числа Простое число — это натуральное число,
имеющее ровно два различных натуральных делителя: единицу и самого себя. Все
остальные натуральные числа, кроме единицы, называются составными. Ряд простых чисел начинается так: 2,3,5,7,11,13,17… Любое натуральное число, большее единицы, представимо в виде произведения степеней простых чисел, причём единственным способом с точностью до порядка следования сомножителей. Например, 121968= 2^4 * 3^2 * 7 * 11^2
Слайд 30
3.2. Целые числа.
Целые числа, получаемые объединением натуральных чисел
с множеством чисел противоположных натуральным и нулём, обозначаются Z={...-2,-1,0,1,2,...}. Любое целое число можно
представить как разность двух натуральных. Целые числа замкнуты относительно сложения, вычитания и умножения (но не деления). Такая алгебраическая структура называется кольцом.
Слайд 31
3.3. Рациональные числа.
Рациональные числа — числа, представимые в виде дроби m/n (n ≠
0), где m — целое число, а n — натуральное число. Рациональные числа замкнуты уже
относительно всех четырёх арифметических действий: сложения, вычитания, умножения и деления (кроме деления на ноль). Для обозначения рациональных чисел используется знак Q (от англ. quotient).
Слайд 32
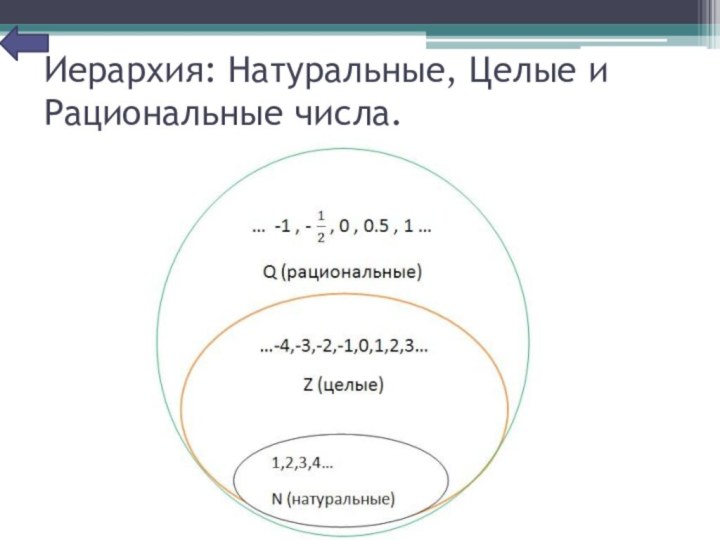
Иерархия: Натуральные, Целые и Рациональные числа.
Слайд 33
3.4. Действительные числа.
Действительные (вещественные) числа представляют собой расширение множества рациональных чисел,
замкнутое относительно некоторых (важных для математического анализа) операций предельного
перехода. Множество вещественных чисел обозначается R . Его можно рассматривать как пополнение поля рациональных чисел Q при помощи нормы, являющейся обычной абсолютной величиной. Кроме рациональных чисел, R включает множество иррациональных чисел I не представимых в виде отношения целых.
Слайд 34
3.5. Комплексные числа.
Комплексные числа C, являющиеся расширением множества действительных чисел.
Они могут быть записаны в виде z=x+iy, где i — т. н. мнимая
единица, для которой выполняется равенство i^2 = -1 Комплексные числа используются при решении задач электротехники, гидродинамики, картографии, квантовой механики, теории колебаний, теории хаоса, теории упругости и многих других. Комплексные числа подразделяются на алгебраические и трансцендентные. При этом каждое действительное трансцендентное является иррациональным, а каждое рациональное число — действительным алгебраическим.
Слайд 35
Более общими (но всё ещё счётными) классами чисел,
чем алгебраические, являются периоды, вычислимые и арифметические числа (где каждый последующий класс шире, чем
предыдущий).
Для перечисленных множеств чисел справедливо следующее выражение: P ⊂ N ⊂ Z ⊂ Q ⊂ R ⊂ C
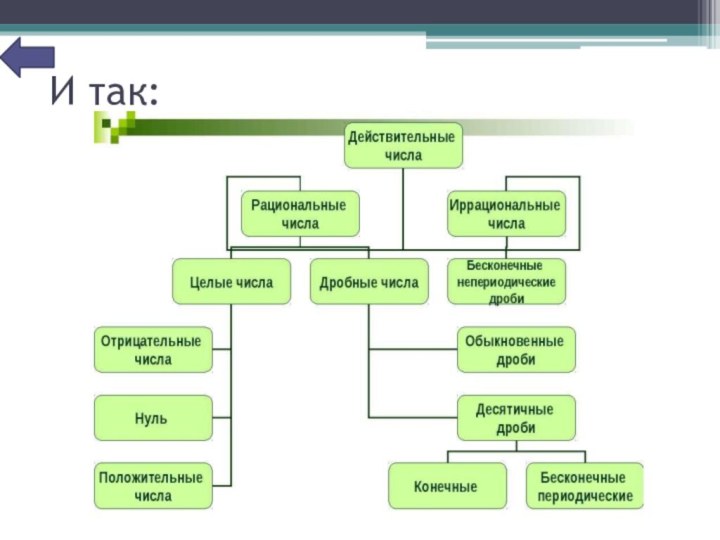
Слайд 37
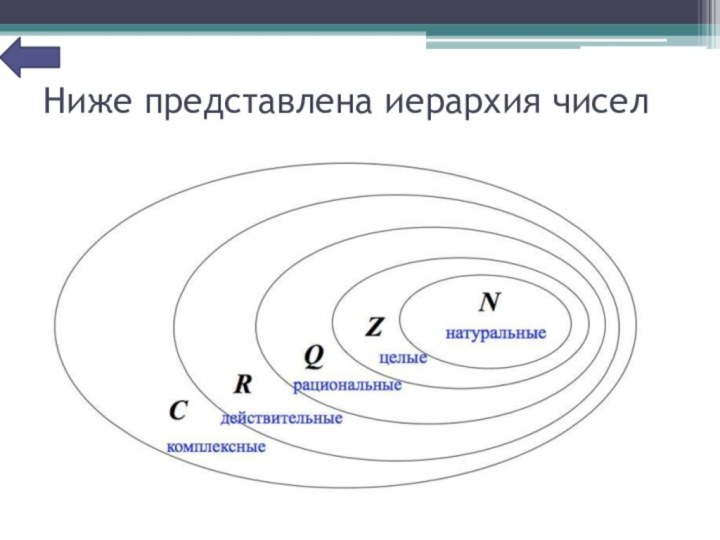
Ниже представлена иерархия чисел
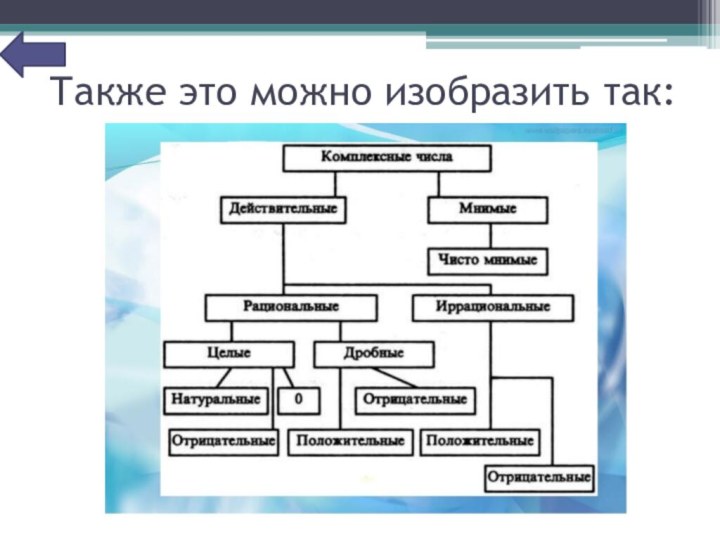
Слайд 38
Также это можно изобразить так: