Слайд 2
Устные упражнения
Верны ли высказывания?
Пропорция-это равенство двух отношений.
В пропорции
2 ׃ 5=10 ׃ 25 числа 2 и 25
называются средними членами пропорции.
Произведение крайних членов верной пропорции равно произведению ее средних членов.
Количество товара и его стоимость при постоянной цене являются пропорциональными величинами.
Слайд 3
Решение примеров
1. Выполнить деление дробей
Слайд 4
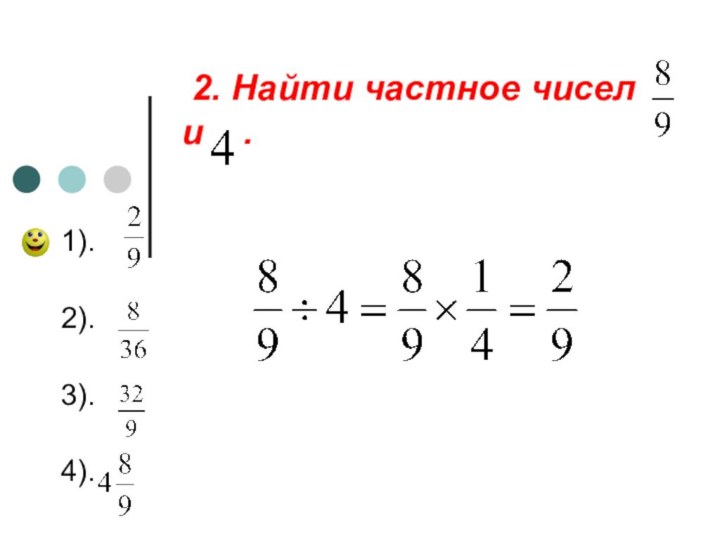
2. Найти частное чисел и
.
1).
2).
3).
4).
Слайд 5
3. Найти значение выражения
1).
2).
3).
4).
Слайд 6
4. Указать пару взаимно обратных чисел
1). 0,4
и
2). и
3). 1 и 0
4). и
Слайд 7
5. Какое равенство неверно?
1).
2).
3).
4).
Слайд 8
6. При каком значении буквы верно равенство
=
?
1). Х= 5
2). Х = 25
3). Х = 8
4). Ни при каком
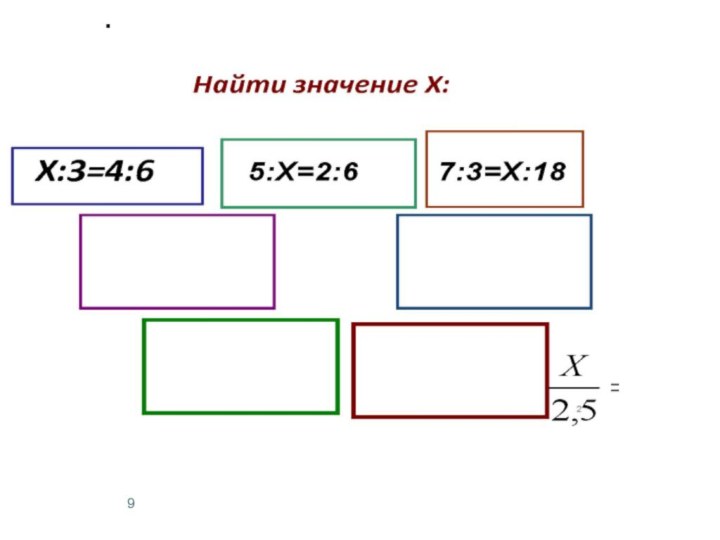
Слайд 10
План решения задач с помощью пропорций:
1.Составление краткой записи
к условию задачи.
2.Определение вида пропорциональной зависимости.
3.Составление пропорции.
4.Нахождение неизвестного члена
пропорции.
5.Проверка ответа по смыслу.
Слайд 11
1. В 2,5 кг сиропа содержится 1,2 кг
сахара. Сколько сахара содержится в 3 кг такого же
сиропа?
Сироп Сахар
2,5 кг - 1,2 кг
3 кг - х кг
Решите задачу с помощью пропорции:
Слайд 12
2.Из 30 кг свежих яблок выходит 10,5 кг
сушеных. Сколько надо взять свежих яблок, чтобы получить 14,7
кг сушеных?
Решите задачу с помощью пропорции:
Свежие яблоки Сушеные яблоки
30 - 10,5 кг
х кг - 14,7 кг
Слайд 13
3.Со 125 гусей получают 4 кг пуха. Сколько
пуха можно получить с 875 гусей?
Решите задачу с помощью
пропорции:
Решите, пожалуйста, сами.
Слайд 14
У : 0,8 = 3,5 : 0,5
0,5
*У = 0,8 * 3,5
У = 0,8 * 3,5
*0,5
У = 1,4
Найди ошибку в решении уравнения.
Слайд 15
4. Поезд, скорость которого 45 км/ч, затратил на
некоторый участок пути 4 часа. За сколько часов пройдет
этот путь поезд, если его скорость станет 40 км/ч?
Слайд 16
При решении задач на обратно пропорциональную зависимость сначала
нужно подробно разобрать с учащимися составление краткой записи пропорции.
Например, краткая запись задачи про поезд сначала будет выглядеть вот так:
Скорость Время
45 км/ч - 4 ч
40 км/ч - х ч
Далее учащиеся устанавливают вид пропорциональной зависимости в задаче и показывают это с помощью разнонаправленных стрелочек. Так же учащиеся, опираясь на определение обратно пропорциональной зависимости, говорят, что отношение значений скорости должно быть равно обратному отношению значений времени движения поезда. Таким образом, краткая запись и пропорция будут выглядеть так:
Скорость Время
45 км/ч - 4 ч
40 км/ч - х ч
Составлю и решу пропорцию:
Слайд 17
4 комбайнера могут убрать пшеницу с поля за
10 дней. За сколько дней уберут это поле 5
таких же комбайнеров?
Решите задачу с помощью пропорции:
«пропорция» (от латинского proportio) означает «соразмерность», «определённое соотношение частей
между собой»
Учение о пропорциях особенно успешно развивалось в IV в. до н. э. в Древней Греции
С пропорциями связывались представления о красоте, порядке и гармонии
Слайд 19
Целое всегда состоит из отношении друг к
другу и к целому. Принцип золотого сечения – высшее
проявление совершенства целого и его частей в искусстве, науке, технике и природе. частей, части разной величины находятся в определенном
Слайд 20
Принято считать, что понятие о золотом делении ввел
в научный обиход Пифагор, древнегреческий философ и математик (VI
в. до н.э.). Но есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян.
И действительно, пропорции пирамид, предметов быта и украшений свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании
Слайд 21
Греческий скульптор Леохар создал знаменитую статую Аполлона
Бельведерского, воплотившую представление древних греков о красоте. Если высоту
статуи разделить в отношении золотого сечения и то же самое проделать с каждой частью, то точки деления придутся на талию, коленную чашечку, адамово яблоко. Та же закономерность распространяется в отдельности на лицо, руку, кисть.
Слайд 22
Великий древнегреческий скульптор Фидий часто использовал “золотое
сечение” в своих произведениях. Его статуя Зевса Олимпийского, считалась
одним из чудес света
Слайд 23
Афина Парфенос (Афина Дева)- всемирно известная статуя Фидия,
созданная по законам «божественной пропорции».
Слайд 24
Статуя Афины Парфенос дала название Парфенону –
одному
из самых величественных храмов Древней
Греции.
Отношение высоты здания
к его длине равно 5:8 .
Если произвести деление Парфенона по «золотому
сечению», то получим те или иные выступы фасада.
Слайд 25
Задача
Длина Парфенона
69,54 м. Найдите высоту
храма, если его высота относится
к длине
по правилу «золотого сечения», т.е. в
отношении 5 : 8 .
Слайд 26
Краткое условие задачи
Размеры
Части
Ширина x м. 5
Длина 69.54 м. 8
Слайд 27
Решение.
X : 69,54= 5:8
8X= 69,54 * 5
X=69,54 *
5 : 8
X= 347,7 : 8
X= 43,4625
Слайд 28
Говоря о примерах «золотого сечения», нельзя не остановить
своего внимания на творчестве Леонардо да Винчи. Он снискал
славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в.
Слайд 29
Нет сомнений, что Леонардо да Винчи был великим
художником, это признавали уже его современники. Именно Леонардо да
Винчи, пользуясь «золотым сечением», создал учение об идеальных пропорциях человеческого тела.
Слайд 30
Портрет Моны Лизы (Джоконды) работы Леонардо да Винчи
долгие годы привлекает внимание исследователей, которые обнаружили, что композиция
рисунка основана на золотых треугольниках, т.е. с использованием «золотого сечения».
Слайд 31
В 1855 г. немецкий исследователь золотого сечения профессор
Цейзинг опубликовал свой труд “Эстетические исследования”. Подверглись исследованию греческие
вазы, скульптуры, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. И везде присутствовало «золотое сечение».
Слайд 32
В ХХ-ХХI веках принцип золотого сечения широко применяется
в живописи, архитектуре, скульптуре…
«Чёрный квадрат» Казимира Малевича выполнен по
законам «божественной пропорции», может быть в этом и скрыта его загадка
Слайд 33
С давних времён размеры книг находились в отношении
золотого сечения ( примерно 5:8 ). Найдите
длину книги, если её ширина равна 13 см.
Слайд 34
Краткое условие задачи.
Размеры
Части
Ширина 13см 5
Длина Xсм 8
Слайд 35
Решение.
13 : x = 5 : 8
5x
= 13*8
X= 13*8 : 5
X = 20,8
Слайд 36
Золотое сечение в математике
Золотое сечение – это такое
пропорциональное деление отрезка на неравные части, при котором весь
отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b = b : c или с : b = b : а.
Рис. 1.
Геометрическое изображение золотой пропорции
Слайд 37
Золотое сечение в природе
Рассматривая расположение листьев на стебле
растений можно заметить, что между каждыми двумя парами листьев
(А и С) третья расположена в месте золотого сечения (В).