красотой - красотой отточенной и строгой, возвышенно чистой и
стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.Бертран Рассел
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


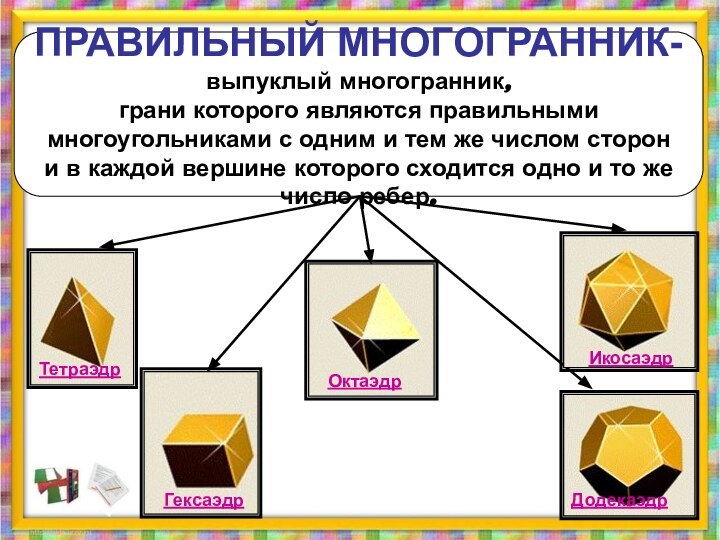







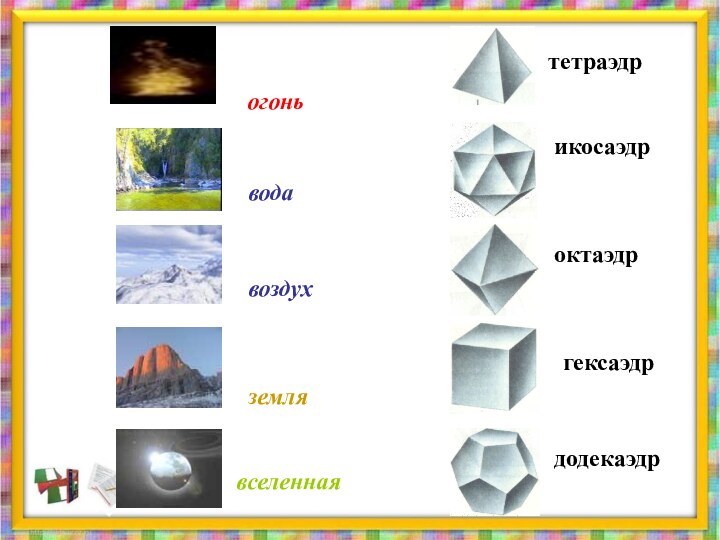

















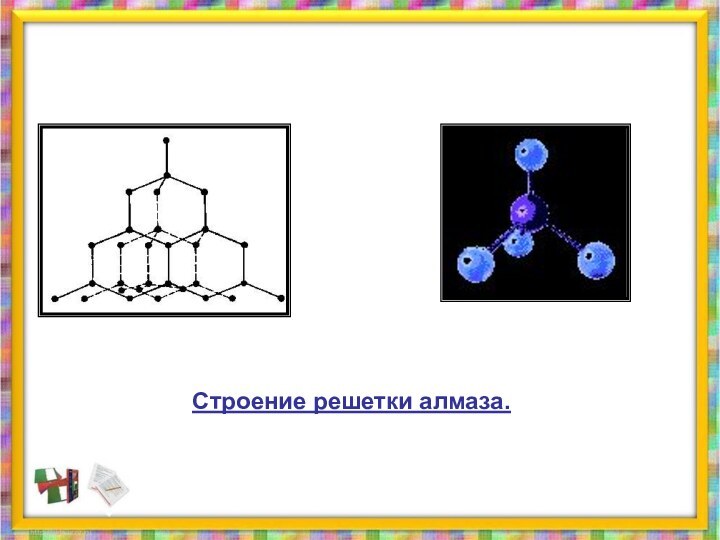
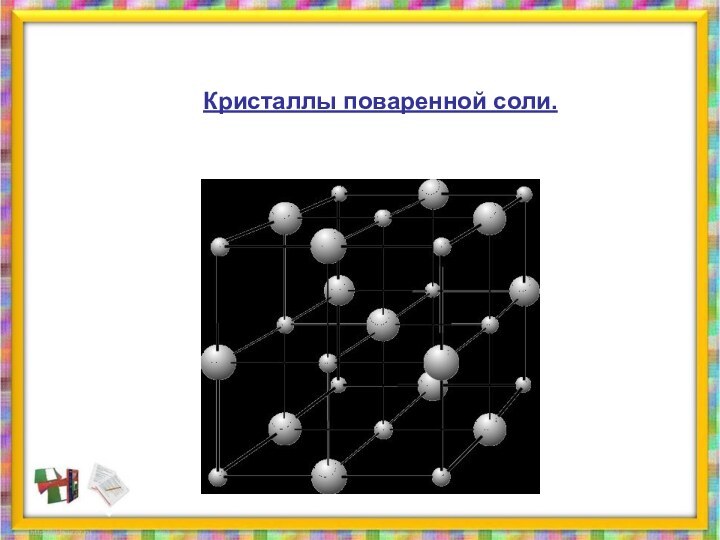
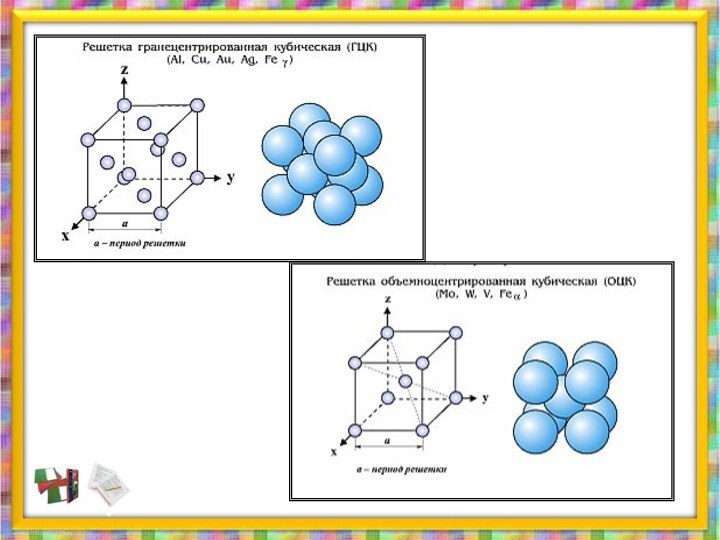


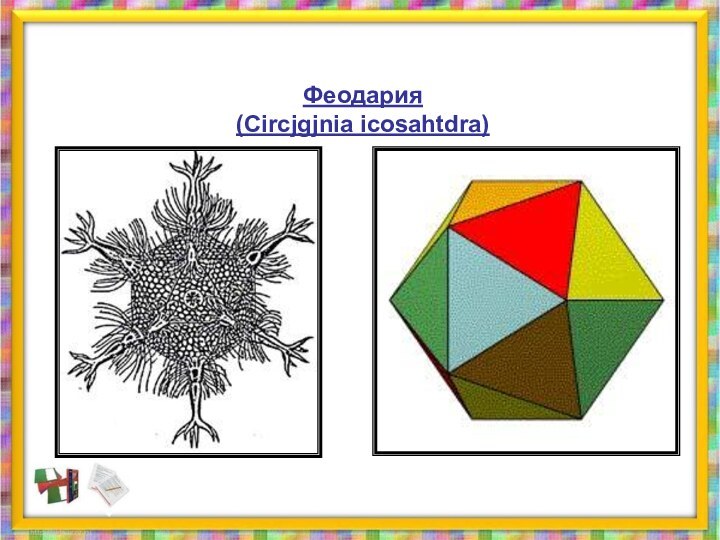







Гексаэдр
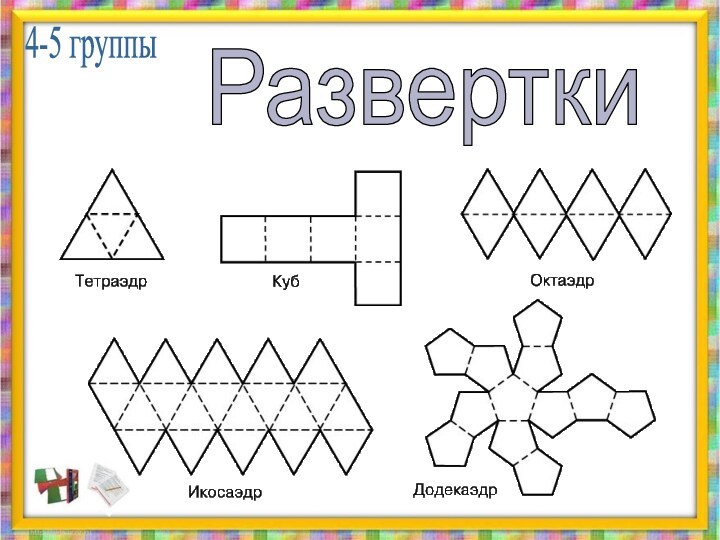
Тетраэдр
Октаэдр
Додекаэдр
Икосаэдр
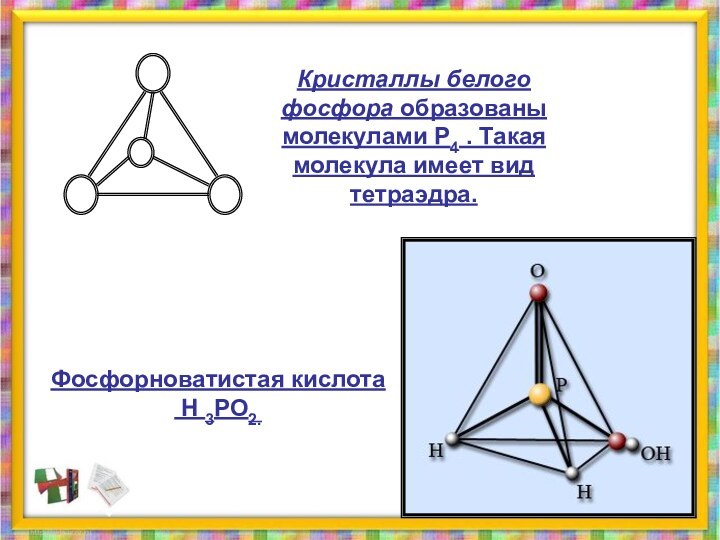
ТЕТРАЭДР
КУБ (ГЕКСАЭДР)
ИКОСАЭДР
3 группа- вывести формулы для нахожденияплощадей
поверхности прав. многогранников.
4 и 5 группы- составить развёртки правильных
многогранников.
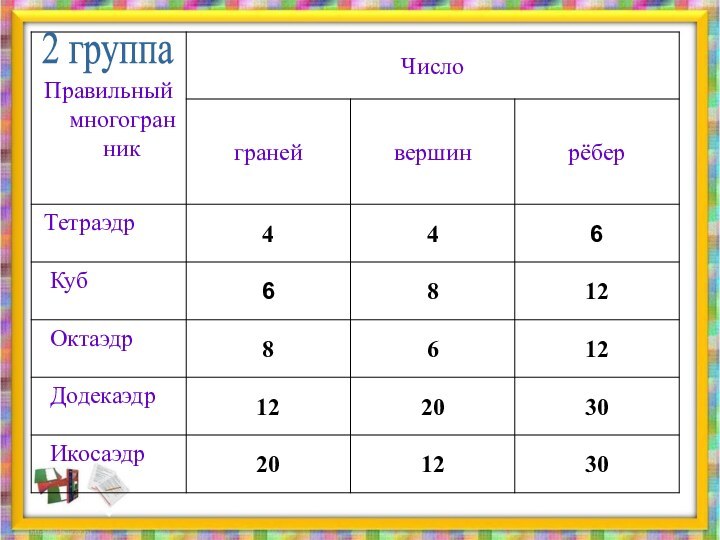
1 группа
2 группа
Архимедовы тела