Презентация на тему по математике на тему Некоторые приемы устного счета. Умножение

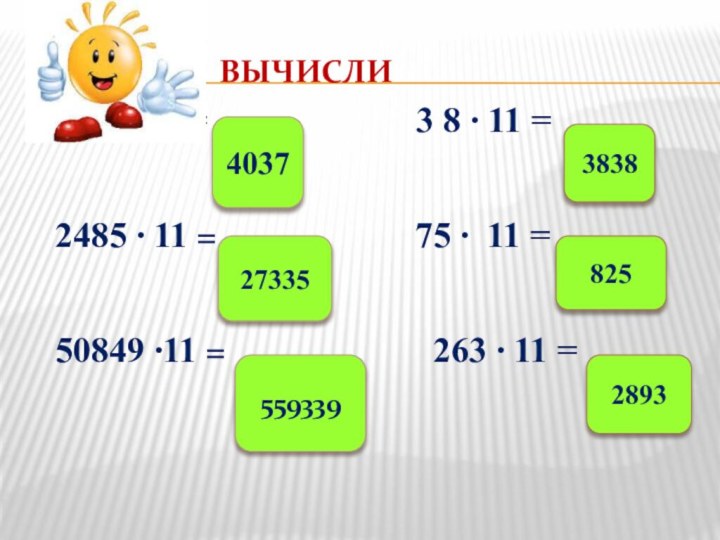
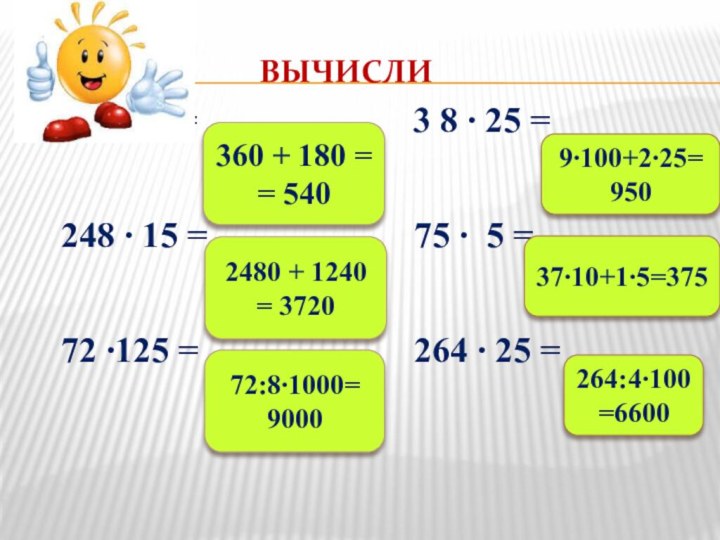
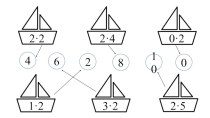
Учебная цель: Изучить некоторые приемы устного счета. Применить их при вычислениях.
Развивающая цель: Развитие внимания, памяти, сообразительности учащихся.
Воспитательная цель: Воспитание уважения друг к другу, уверенности в себе. Способствовать выработке у учащихся желания и потребности изучения математики.

свойства умножения a∙ (b+c) = a∙b

+ a∙c  

   52 · 11 = 52 · (10+1) = 520 + 52 = 572
43 ∙ 11 = 43 ∙ (10+1) =
706 ∙ 11 = 706 ∙ (10+1) =
38 ∙ 11 =
434 ∙ 11 =

25∙11
 При умножении вторая цифра множителя 25 будет последней цифрой

произведения (5);
средняя цифра произведения равна сумме цифр множителя 25 (2 + 5 = 7);
первая цифра множителя 25 будет первой цифрой произведения (2).
25 ∙ 11 = 2(2+5)5 = 27
81 ∙ 11 =8(8+1)5 =
354 ∙ 11 = 3(3+5)(5+4)4 = 3894
815 ∙ 11 = 8(8+1)(1+5)5 =
2134 ∙ 11 = 2(2+1)(1+3)(3+4)4 = 23474
5452 ∙ 11 = 5(5+4)(4+5)(5+2)4 =



   

= 14 - 4 –вторая цифра произведения, 1

в уме; 6 да 1 в уме будет 7 - первая цифра произведения. 68 ∙ 11 = 6(6+8)8 = 748 478 ∙ 11 = 4(4+7)(7+8)8 = 5258 89056 ∙ 11 = 8(8+9)(9+0)(0+5)(5+6)6 = 979616

При умножение на 11 , когда сумма двух рядом стоящих цифр первого множителя больше или равна 10, то цифру десятков прибавляют к следующей старшей цифре множителя. Причем, сложение цифр надо производить только с конца.

Пример 1. 68 ∙ 11

3 8 ∙ 11 =
2485 ∙ 11 = 75 ∙ 11 =
50849 ∙11 = 263 ∙ 11 =

4037

27335

559339

3838

825

2893

1111.
Умножение на 111, на 1111 аналогично умножению на11. Мысленно

раздвигаем цифры первого сомножителя 42 (4…2), предварительно найдя сумму его цифр 4+2=6, и вставляем полученную сумму, повторив эту операцию дважды ( или трижды соответственно):
42x111= 4(4+2)(4+2)2 = 4662

39×111= 3(3+9)(3+9)9 =
72×1111= 7(7+2)(7+2)(7+2)2 = 79992
35×1111=3(3+5)(3+5)(3+5)5 =

используя распределительный закон:
58 ∙ 101 = 58∙(100+1)= 58 ∙

100 + 58 ∙ 1 = 5800 + 58 = 5858
2 способ
Чтобы умножить двузначное число на 101 , надо мысленно приписать к данному числу ( справа или слева) еще раз само это число.
54 ∙ 101 = 5454 24 ∙ 101 = 87 ∙ 101 =

используя распределительный закон:
548 ∙ 1001 = 548∙(1000+1)= 548 ∙

1000 + 548 ∙ 1 = 548000 + 548 = 548548
2 способ
Чтобы умножить трехзначное число на 1001 , надо мысленно приписать к данному числу ( справа или слева) еще раз само это число.
256 ∙ 1001 = 256256 789 ∙ 1001 =

3 8 ∙ 1111 =
28 ∙ 101 = 75 ∙ 101 =
59 ∙111 = 635 ∙ 1001 =

3774

2828

6549

42218

7575

635635

5 ∙ 2 = 10 25 ∙ 4 = 100 125 ∙ 8 = 1000




46 ∙ 5 = 46:2 ∙ 10 = 230; 14 ∙ 5 = 48 ∙ 25 = 48:4 ∙ 100 = 1200; 28 ∙ 25 =
32 ∙ 125 = 32:8 ∙ 1000 = 4000. 56 ∙ 25 =

Чтобы умножить число на 5, 25, 125 надо разделить это число соответственно на 2, 4, 8 и результат умножить на 10, 100, 1000.

или 8, то деление производится с остатком. Затем частное умножают

соответственно на 10, 100, 1000, а остаток на 5, 25, или 125.

1) 53∙5 = 26 ∙ 10 + 1 ∙ 5 = 265
53: 2 = 26 и 1 в остатке;
2) 43 ∙ 25 = 10 ∙ 100 + 3 ∙ 25 =1075
43:4 = 10 и в остатке 3;
3) 66 ∙ 125 = 8 ∙ 1000 + 2 ∙ 125 = 8250
66:8 = 8 и в остатке2.

3 8 ∙ 25 =
248 ∙ 15 = 75 ∙ 5 =
72 ∙125 = 264 ∙ 25 =

360 + 180 = = 540

2480 + 1240 = 3720

72:8∙1000= 9000

9∙100+2∙25=950

37∙10+1∙5=375

264:4∙100=6600

Умножение на 9, 99 и 999 с помощью применения распределительного закона умножения

286 ∙ 9 = 286 ∙ (10-1) = 2860 – 286 = 2574;
23 ∙ 99 = 23∙(100-1) = 2300 -23 =2277;
18 ∙ 999 = 18∙(1000-1) = 18000 – 18 = 17982.

45

8415

547452

Задача С.В. Рачинского «Умножение на 9, 99 и 999 чисел, имеющих одинаковое количество цифр».

1)от первого множителя надо отнять 1, записать ответ.
2) от второго множителя надо отнять полученную разность, записать ответ.

7 ∙ 9 = (7-1)(9-6) = 63

37 ∙ 99 = (37-1)(99-36) = 3663

127∙ 999 = (127-1)(999-126) = 126873

5 ∙ 9 =

Вычисли сам

85 ∙ 99 =

548 ∙ 999 =

(10a + 5)2 = 100a∙(a + 1) + 25 1)Цифру десятков в числе надо умножить на цифру на 1 больше данной, т.е. 3∙4 =20
2) К полученному результату приписать число 25

752 = (7∙8)25 = 5625.
452 = (4∙5)25 = 2025.
252 = (2∙3)25 =

Возведение в квадрат двузначных чисел, оканчивающихся на 5.

(50 + а)2 =100∙(25 +а) +а2.
1)К числу 25 прибавить

цифру в
разряде единиц, записать ответ.
2)Справа к результату приписать
квадрат числа единиц, чтобы
получилось четырехзначное число.

512 = 100∙(25+1)+ 12 =2601,
582 = 100∙(25+8)+ 82 = 3364,
542 =

Возведение в квадрат двузначных чисел, имеющих 5 десятков.

из тождества (10а +b)(10с + d) = 100ас +10(аd + bc) + bd.
Для

получения единиц произведения перемножают единицы множителей, для получения десятков умножают десятки одного на единицы другого множителя и наоборот и результаты складывают, для получения сотен перемножают десятки.

37∙ 48 =(3∙4)(3∙8+7∙4)(7∙8) = 1776

Этот способ умножения основан на тождестве

(10 + a)∙(10 + b) = 100 + 10∙(a + b) + ab
12∙17 = 100 + (2+7)∙10 + 2∙7 = 204
К числу 100 прибавить произведения:
- Сумму единиц числа умножить на 10;
- Перемножить единицы;


13∙19 = 100 + (3+9)∙10 + 3∙9 =

542 =
18 ∙ 14 = 152 =
572 = 652 =

240

252

100∙(25+7)+72 = 3249

100 ∙(25+4)+42 = 2916

(1∙2)25=225

(6∙7)25=4225

1209

7216

4224

31 ∙ 39 =

Вычисли сам

82 ∙ 88 =

64 ∙ 66 =

Умножение чисел, сумма цифр единиц которых равна 10, а число десятков одинаково

Этот способ умножения основан на тождестве
(10a+b)(10a+c) = 100a∙(a+1) + bc
43 ∙ 47 = (4 ∙ 5)(3 ∙ 7) = 2021
1)Цифру десятков а умножить на число, большее данного на 1. Записать результат.
2)Справа приписать произведение единиц множителей.

сомножитель увеличить в несколько раз, а другой уменьшить во

столько же раз, то произведение не измениться.
Примеры:
43 ∙ 16 = 86∙ 8 = 172∙ 4 = 344∙ 2 = 688 ∙ 1 = 688
23 ∙ 27 = 69 ∙ 9 = 207 ∙ 3 = 621 ∙ 1 = 621
125 ∙ 24 = 500 ∙ 6 = 1500 ∙ 2 = 3000 ∙ 1 = 3000

=
53 ∙ 16 =
34 ∙ 18 =
45 ∙

24 =
37 ∙ 32 =

74 ∙ 4 = 148 ∙ 2 = 296 ∙ 1 = 296

106 ∙ 8 = 212 ∙4 =424∙2 =848∙1= 848

68 ∙ 9 = 204 ∙ 3 = 612 ∙ 1 = 612

90∙12 = 270∙4 =540∙2=1080∙1= 1080

74∙16 = 148∙ 8 = 296∙4 = 592 ∙2 = 1184 ∙ 1 = 1184

на счетных приборах».
2. Виленкин Н.Я, Жохов В.И, Чесноков А.С,

Шварцбурд С.И. Математика 5 класс.
3. Б.А. Кордемский «Математическая смекалка».
4. Ф.Ф. Нагибин «Математическая шкатулка».
5. Журнал «Математика в школе»