Презентация на тему 7 способов решения тригонометрического уравнения

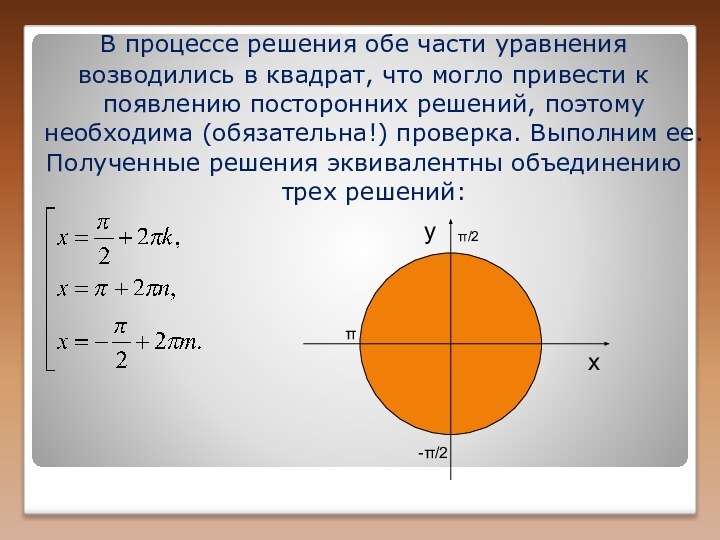
выразительности,
стройности математических формул,
решении задач различными способами,
изяществе математических доказательств,
порядке,
богатстве приложений

универсальных математических методов.

Проблема красоты привлекала и привлекает величайшие умы человечества.

форм ,наглядной выразительности математических объектов, восприятие которых сопряжено с

наименьшими усилиями. Ее привлекательность будет усиливаться за счет эмоционально-экпрессивной составляющей -

оригинальности,
неожиданности,
изящества.

Математики живут ради тех славных моментов,
когда проблема оказывается решенной,
ради моментов

озарения, восторга

его исследователем!

уже говорили о богатстве приложений универсальных математических методов. При

решении уравнений одним из них является метод разложения на множители.
Можно ли применить его к решению уравнения
Sin x –cos x = 1?
На первый взгляд,кажется что нет…

А если использовать специфические тригонометрические преобразования

ноль,мы выделили
выражение 1 + cos x …
Как вы думаете

зачем

Рассуждаем

Преобразуем исходное уравнение
Sin x – cos x = 1
к виду
Sin x – ( 1 + cos x) = 0.

формулу повышения степени
и формулу двойного аргумента

Итак…

один из множителей равен нулю, а остальные при этом

не теряют смысла, поэтому









однородное уравнение первой степени.

противоречит тождеству


Получим



Ответ:

левую часть по формулам двойного
аргумента, а правую часть заменим
тригонометрической

единицей:

2-й способ

И так далее, как в предыдущем способе …

способы преобразования разности (или суммы) тригонометрических функций в произведение:





Но

увы, в левой части уравнения, мы видим разноименные функции. Как изменить название функции на «кофункцию» ?
Есть изящный способ!!!



Всего лишь нужно применить формулу приведения!

произведение.
sinx-cosx=1
Запишем уравнение в виде:

Применяя формулу разности двух синусов, получим






Ответ:

3-й способ:

из функций
Так как



Возведем обе части полученного уравнения в квадрат

в квадрат, что могло привести к появлению посторонних решений,

поэтому необходима (обязательна!) проверка. Выполним ее.
Полученные решения эквивалентны объединению трех решений:

х

у

π/2

π

-π/2

с ранее полученными, поэтому не являются посторонними.
Проверим


Левая

часть:


Правая часть:1.

Следовательно,

подстановка) по формулам:





С учетом приведенных формул уравнение
sinx-cosx=1
запишем в виде

все множество R.

переходе к
из

рассмотрения выпали значения, при которых
не имеет смысла, т.е.


Следует проверить, не является ли х=π+2πk решением данного уравнения.
Левая часть:
sin(π+2πk)-cos(π+2πk)=sinπ-cosπ=0-(-1)=1.
Правая часть: 1.
Значит, х=π+2πk, k€Z – решение уравнения.
Ответ:

и специфические. Наиболее ярким из них является метод введения

вспомогательного угла (числа).
Благодаря этому приёму исходное уравнение легко сводится к простейшему –



Последний метод, предлагаемый нами, связан также с нестандартным преобразованием тригонометрического уравнения – возведением обеих частей в квадрат.
И хотя он является коварным в плане приобретения посторонних корней, но подкупает своим оригинальным способом сведения исходного уравнения к простейшему!

просто и красиво!

за скобку ( корень квадратный из

суммы квадратов коэффициентов при sinx и cosx). Получим









Ответ:

что первое и четвертое решения – посторонние.

Ответ:

x

0

y

π/2

π

-π/2