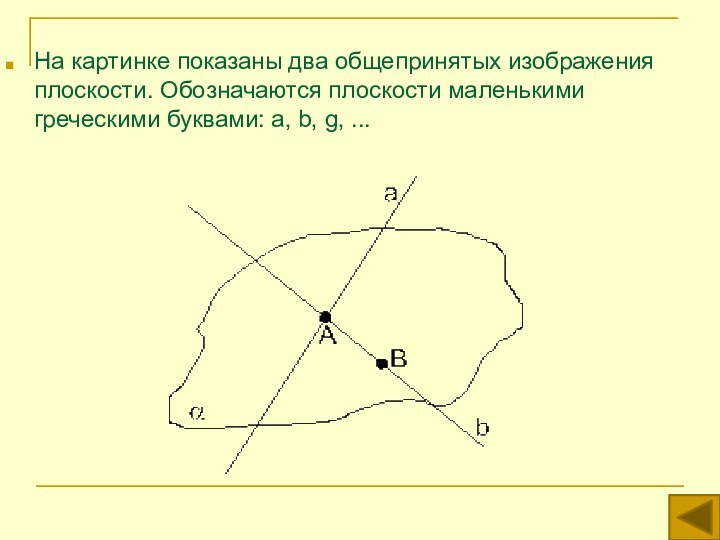
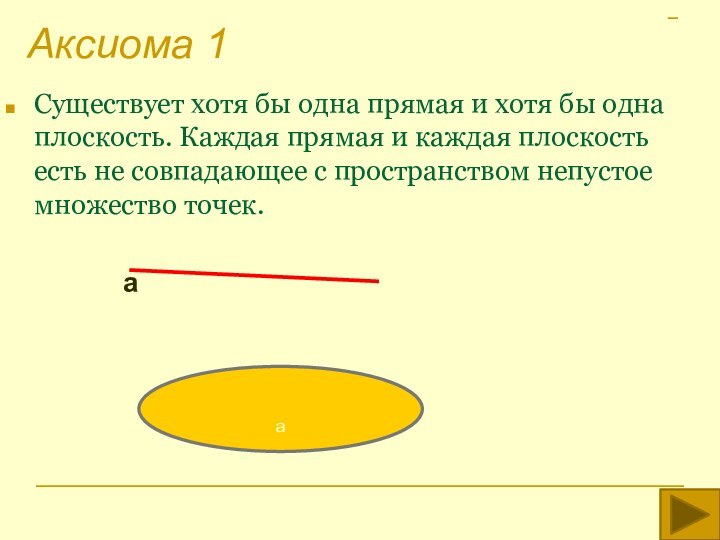
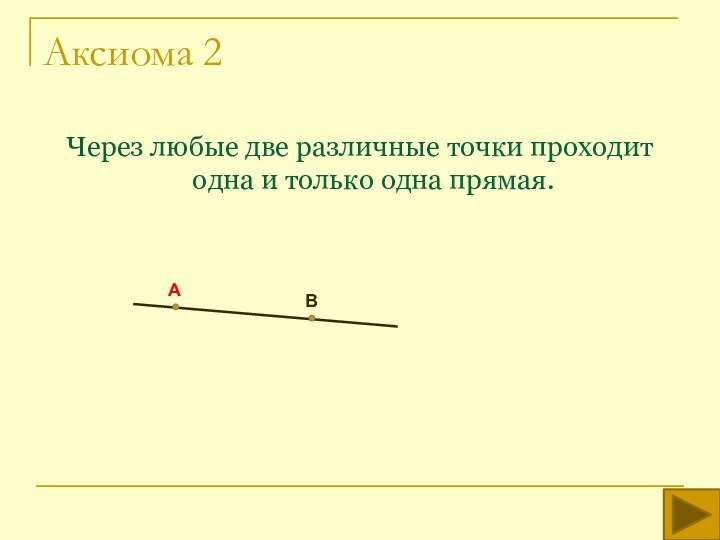
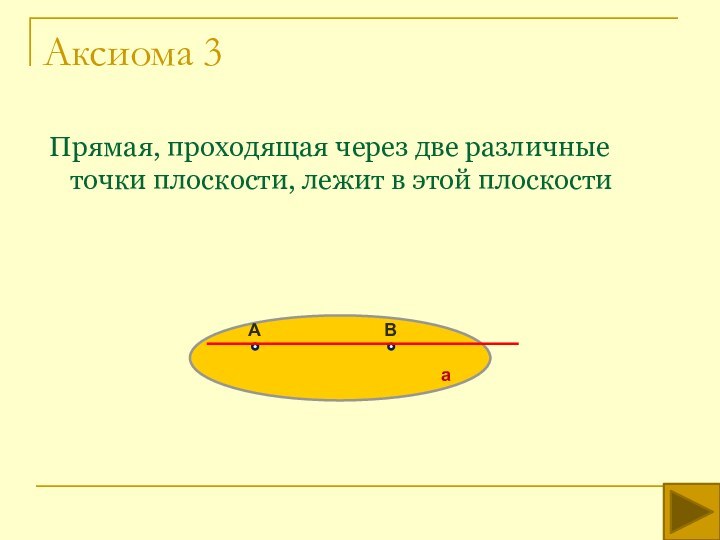
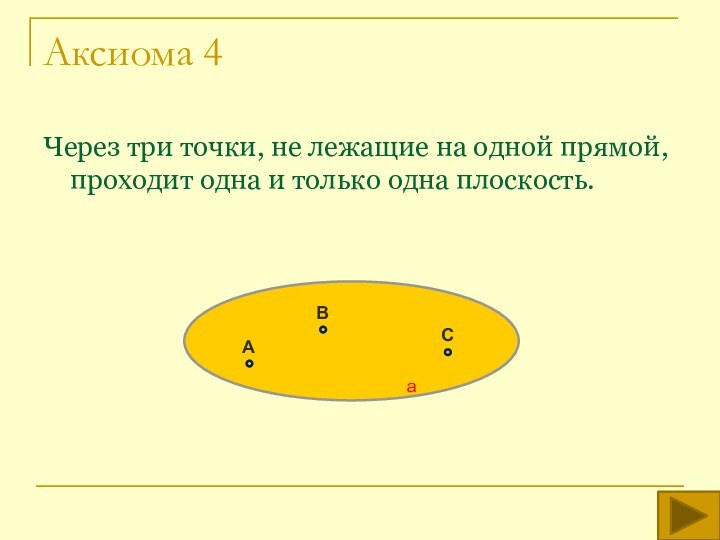
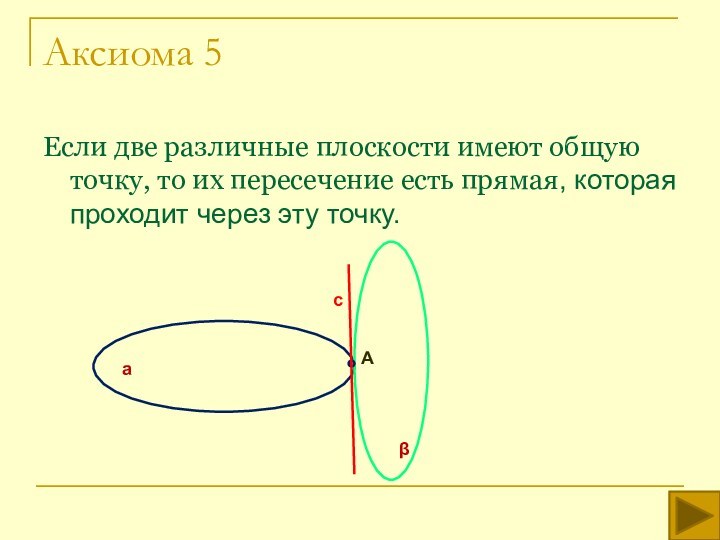
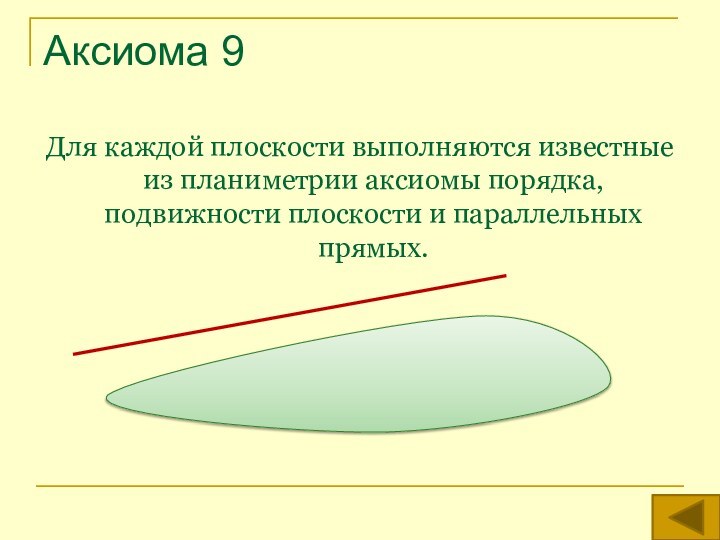
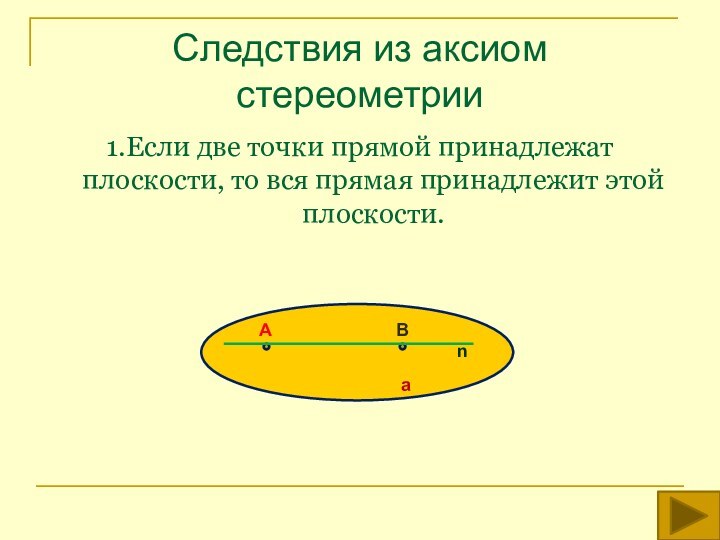
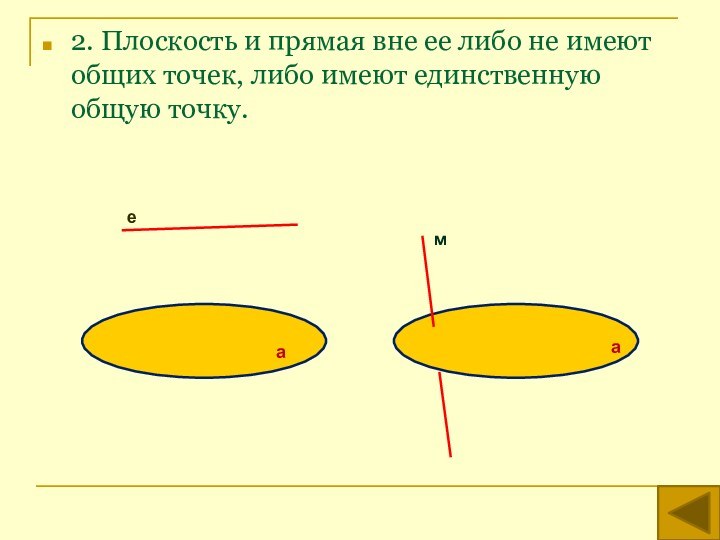
аксиом планиметрии и трех аксиом стереометрии .
В аксиомах стереометрии выражены основные свойства неопределяемых понятий: точки, прямой, плоскости и расстояния.Плоскости - это фигуры, на которых выполняется планиметрия и для которых верны аксиомы стереометрии.
Пространство - это множество, элементами которого являются точки и в котором выполняется система аксиом стереометрии, описывающая свойства точек, прямых и плоскостей.
Стереометрия – раздел геометрии, в котором изучаются свойства фигур в пространстве