- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Арифметическая прогрессия. Формула n-го члена арифметической прогрессии
Содержание
- 2. ИСТОРИЧЕСКАЯ СПРАВКА Задачи
- 3. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯУчитель математики Кажкенова Раушан БатаевнаГУ «Окжетпесская средняя школа Бурабайского района »
- 4. УСТНАЯ РАБОТА
- 5. УСТНАЯ РАБОТА
- 6. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
- 7. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
- 8. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
- 9. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
- 10. КАКАЯ ЗАКОНОМЕРНОСТЬ НАБЛЮДАЕТСЯ В КАЖДОЙ ПОСЛЕДОВАТЕЛЬНОСТИ?
- 11. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯАрифметической прогрессией называется последовательность, каждый
- 12. d=an+1-an
- 13. ПОСЛЕДОВАТЕЛЬНОСТИ ЗАДАНЫ НЕСКОЛЬКИМИ ПЕРВЫМИ ЧЛЕНАМИ? ЕСТЬ ЛИ
- 14. КАКОЙ ВЫВОД ИЗ ЭТИХ ПРОГРЕССИЙ МОЖНО СДЕЛАТЬ?
- 15. ЗАДАЧА.
- 16. ФОРМУЛА N-ГО ЧЛЕНАa1 a2=a1+d a3=a2+d=(a1+d)+d
- 17. ЗАДАЧА.
- 18. РАЗМИНКА72 - 52× 3 24 : 4+
- 19. ОТВЕТЫ К ТЕСТУ:
- 20. Скачать презентацию
- 21. Похожие презентации
ИСТОРИЧЕСКАЯ СПРАВКА Задачи на обе прогрессии встречаются у вавилонян, в египетских папирусах, в древнекитайском трактате «Математика в 9 книгах». Архимед знал, что такое геометрическая прогрессия и умел вычислять сумму любого числа его



















Слайд 3
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Учитель математики
Кажкенова Раушан Батаевна
ГУ «Окжетпесская средняя
школа Бурабайского района »
Слайд 11
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Арифметической прогрессией называется последовательность, каждый член
которой, начиная со второго, равен предыдущему, сложенному с одним
и тем же числом. (an) - арифметическая прогрессия,
если an+1 = an+d ,
где d-некоторое число.
Слайд 13 ПОСЛЕДОВАТЕЛЬНОСТИ ЗАДАНЫ НЕСКОЛЬКИМИ ПЕРВЫМИ ЧЛЕНАМИ? ЕСТЬ ЛИ СРЕДИ
НИХ АРИФМЕТИЧЕСКИЕ ПРОГРЕССИИ?
1) 1; 4; 7; 10;...
2) 1;
4; 15; 18;...3) 1; -1; -3; -5;…
4) 4; 4; 4; 4;…
Слайд 16
ФОРМУЛА N-ГО ЧЛЕНА
a1
a2=a1+d
a3=a2+d=(a1+d)+d =a1+2d
a4=a3+d=(a1+2d)+d=a1+3d
a5=a4+d=(a1+3d)+d=a1+4d
……………………..
an=a1+(n-1)d
an=a1+d
(n-1)
Слайд 18
РАЗМИНКА
72 - 52
× 3
24
: 4
+ 12
: 2
?
72
18
30
15
6 м
20 см : 31
+ 30 см
× 4
- 1 м 60 см
?
20 см
20 см
50 см
2 м
: 2
40 см
Слайд 19
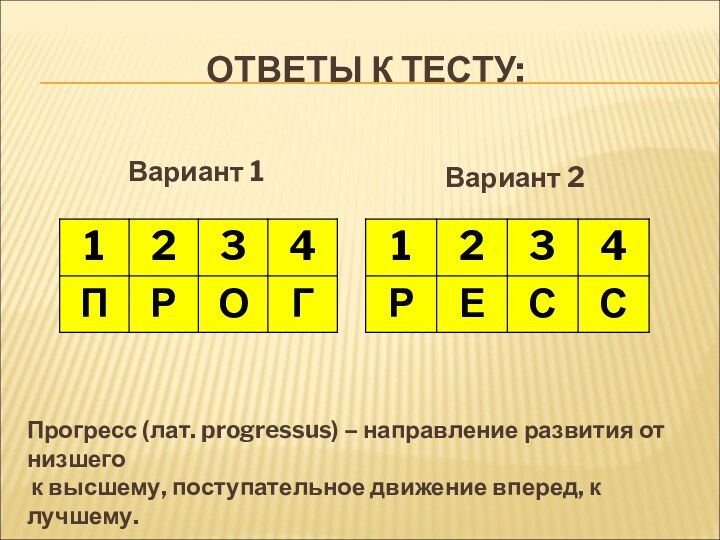
ОТВЕТЫ К ТЕСТУ:
Вариант 1
Вариант
2Прогресс (лат. progressus) – направление развития от низшего
к высшему, поступательное движение вперед, к лучшему.





























