Презентация на тему Аттестационная работа. Занимательная математика

«Занимательная математика»
Автор: Конева Надежда Александровна, МБОУ БГО СОШ №4.
Школа

работает в две смены, имеет 31 класс-комплект при наполняемости 25-30 человек. Общая численность учащихся остается стабильной (820 – 900 учащихся).
Цель и задачи работы: осуществить межпредметные связи математики с историей, литературой, изобразительным искусством, информатикой и другими науками; способствовать воспитанию интереса учащихся к математике; стимулировать у учащихся желание больше узнавать по предмету; пользоваться различными источниками информации; учиться строить свою учебную деятельность.
Формы проектной деятельности: индивидуальная и групповая
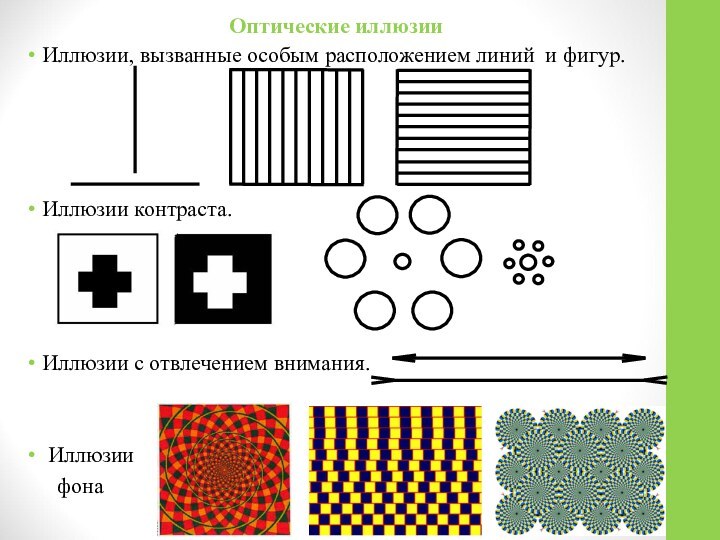
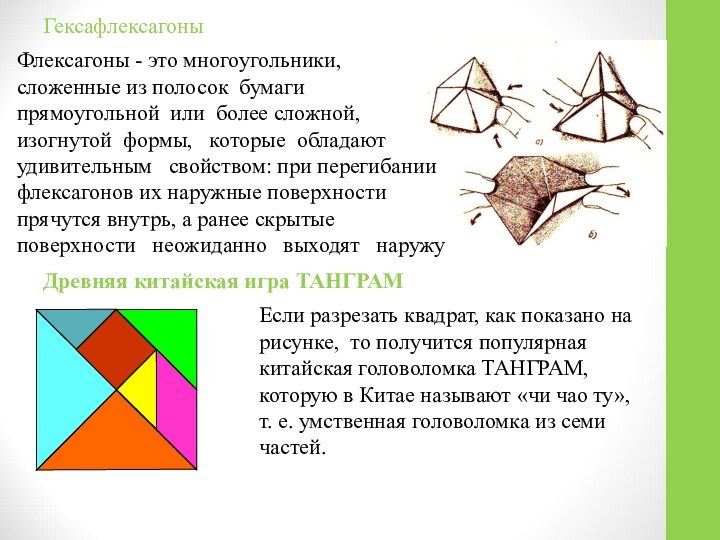
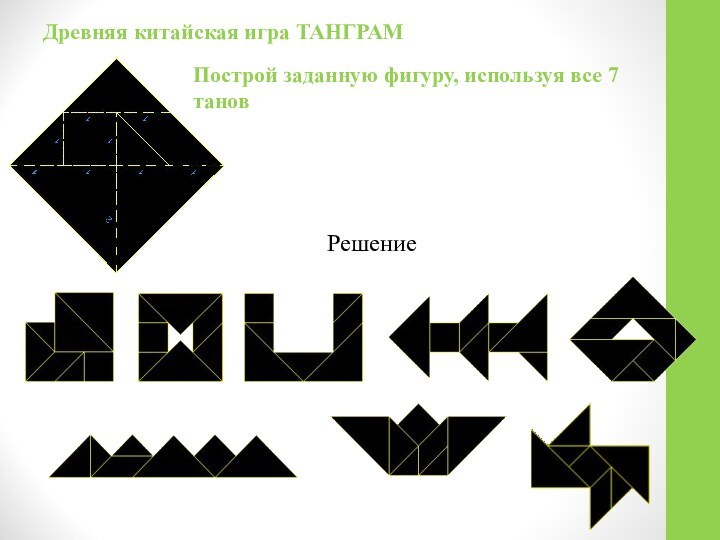
Основное содержание: Решая задачи занимательной математики, ощущаешь красоту и величие математики, осознаёшь всю нелепость широко распространённого, но тем не менее глубоко ошибочного представления о ней как о чем-то унылом и застывшем

накопление статистических данных, их анализ, рефлексия, выявление динамики образовательных

изменений и личных приростов ученика, переопределений цели, уточнение образовательных программ, корректировки хода обучения, прогнозирование дальнейшего развития событий.

Перспективы развития исследовательской/проектной деятельности в учреждении и профессиональной деятельности автора: создание творческих лабораторий, научного общества учеников, развитие дистанционных форм, включение проектной/исследовательской деятельности в предметные рабочие программы

и невозможные фигуры
Цифровые стихи
Заключение
«Занимательная математика»

популяризатор физики, математики и астрономии, один из основоположников жанра

научно – популярной литературы и основоположник занимательной науки, автор понятия «научно-фантастическое». В его библиографии более 1000 статей и заметок, 47 научно-популярных, 40 научно-познавательных книг, 18 школьных учебников и пособий.

Историческая справка

На что способен наш мозг

Читайте текст до конца, не обращая внимание на то, что он как-то не так выглядит... Из исслднеовиай агнлйксиих унёычх селудет, что сошвнерено вёс-рнаво в ккаом пкоярде сотят бвкуы в совле, смаое гавлоне,что перавя и псоленядя бквуы длжоны соттяь на свиох мсеатх. Оталсьное мжеот бтыь ернуодй и ты смжоешь эот порчтиать. Птомоу что мы чтаием солво цлекиом, а не бквуа за бквуой.

с отвлечением внимания.


Иллюзии
фона
Оптические иллюзии

бумаги прямоугольной или более сложной, изогнутой формы, которые

обладают удивительным свойством: при перегибании флексагонов их наружные поверхности прячутся внутрь, а ранее скрытые поверхности неожиданно выходят наружу

Если разрезать квадрат, как показано на рисунке, то получится популярная китайская головоломка ТАНГРАМ, которую в Китае называют «чи чао ту», т. е. умственная головоломка из семи частей.

Древняя китайская игра ТАНГРАМ

китайская игра ТАНГРАМ

правдоподобная ложь

Софизмы и парадоксы
Софизм: Ахиллес, бегущий в 10 раз

быстрее черепахи, не сможет ее догнать. Пусть черепаха на 100 м впереди Ахиллеса. Когда Ахиллес пробежит эти 100 м. черепаха будет впереди него на 10 м. Пробежит Ахиллес эти 10 м, а черепаха окажется впереди на 1 м и т.д. Расстояние между ними все время сокращается, но никогда не обращается в нуль. Значит, Ахиллес никогда не догонит черепаху.

Никто не станет возражать, что 3 -1=6 - 4. Если обе части этого очевидного равенства умножим на (-1), то получим 1-3=4-6. К обеим частям равенства можно прибавить одинаковые числа:1-3+9/4=4-6+9/4. Обе части представляют собой квадраты разностей выражений (1-3/2) и (2-3/2). Из обеих частей извлекаем квадратный корень:1-3/2=2-3/2. К обеим частям прибавим 3/2; имеем на это полное право. Тогда получим 1 = 2.

Арифметический софизм 1=2

в Британском журнале психологии статью о двух классических невозможных

фигурах – невозможном треугольнике и бесконечной лестнице, где невозможный треугольник был представлен в классическом виде - трех соединяющихся под прямым углом балок, изображенных с эффектом перспективы.

Роджер Пентроуз и невозможные фигуры

Литографии Эшера

Восхождение
и спуск

Водопад

4 8 16 9 33 15 98 4 243

Почувствовали ритм и музыку?

Присоединяйтесь.

Цифровые стихи

14.000.000.300 =============== 1  13  29 0  29  35 6  8  40  9  9 5  7  13  25 0  9  9  48 7  300  40  73 15  20  8  8 17  200  33 5.000  30 19 16  200 77 0  50  119 14  17  7 5.000.000  38 16.000  50 6.000.000.000  60 1 11 108