- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Число е
Содержание
- 2. 1111Значениеny11112a – начальная суммаy – состояниеn – период 0.5вернуться
- 3. Значениевернутьсяначало
- 4. Неравенство БернуллиЗначениеТеорема о двух милиционерахДля доказательства:вернутьсяначалоТеорема ВейерштрассаЛюбая монотонная ограниченная после-довательность имеет конечный пределДоказательство
- 5. ДоказательствовернутьсяначалоВ силу неравенства Бернулли:Тогда:
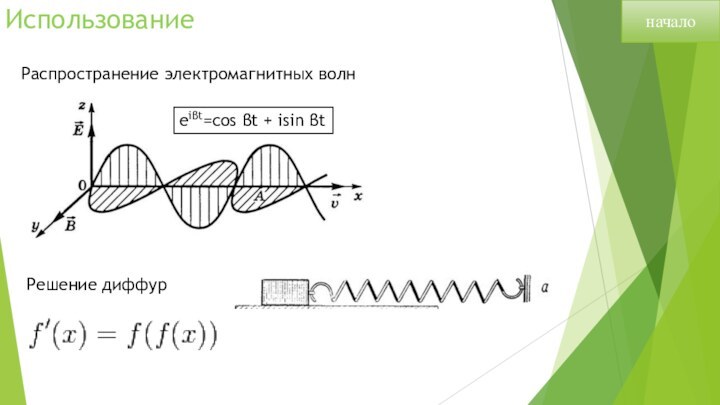
- 6. ИспользованиеначалоРаспространение электромагнитных волнeiβt=cos βt + isin βtРешение диффур
- 7. Способы выраженияначалоМетод цепной дроби;
- 8. Метод цепной дробиначаловернуться
- 9. Скачать презентацию
- 10. Похожие презентации
1111Значениеny11112a – начальная суммаy – состояниеn – период 0.5вернуться