Слайд 2
Оглавление
1. Введение.
2. Элективный курс «Решение задач с параметрами».
а) Пояснительная записка.
б) Структура курса.
в) Краткое содержание курса.
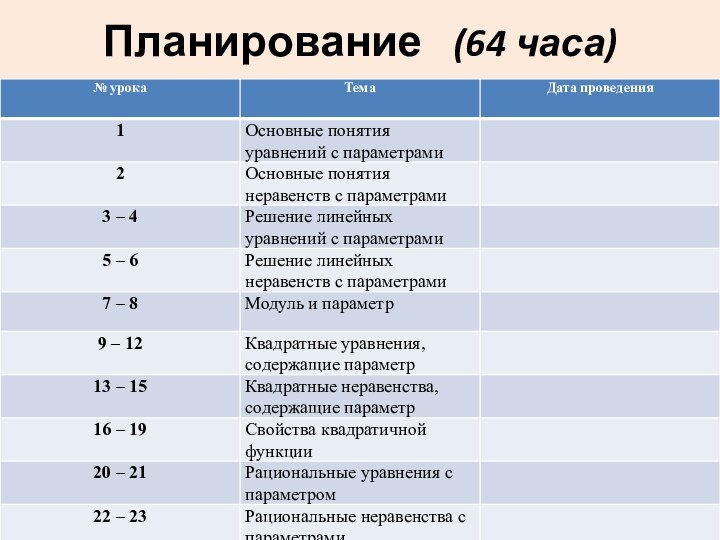
г) Планирование.
д) Методические рекомендации при изучении
некоторых тем.
3. Заключение.
4. Библиографический список.
5. Приложения.
Слайд 3
Профильное обучение:
- базовый общеобразовательный курс;
- профильный
общеобразовательный курс;
-элективные курсы
Слайд 4
Параметр – это переменная, значение которой считается фиксированным,
и каждое значение параметра определяет относительно заданного неизвестного соответствующее
уравнение (неравенство, систему).
Слайд 5
Задачи:
Формирование у учащихся устойчивого интереса к предмету;
Выявление и развитие их математических способностей;
Подготовка к ЕГЭ
и к обучению в ВУЗе.
Слайд 6
Цель курса
Формировать у учащихся умения и навыки по
решению задач с параметрами для подготовки к ЕГЭ и
к обучению в ВУЗе.
Изучение курса предполагает формирование у учащихся интереса к предмету, развитие их математических способностей.
Развивать исследовательскую и познавательную деятельность учащихся.
Обеспечить условия для самостоятельной творческой работы.
Слайд 7
В результате изучения курса учащийся должен:
усвоить основные приемы
и методы решения уравнений, неравенств, систем уравнений с параметрами;
применять алгоритм решения уравнений, неравенств, содержащих параметр;
проводить полное обоснование при решении задач с параметрами;
овладеть исследовательской деятельностью.
Слайд 8
Структура курса
Темы:
Первоначальные сведения. 2ч
Решения линейных уравнений,
содержащих параметры. 2ч
Решения линейных неравенств, содержащих параметры. 2ч
Модуль и параметр. 2ч.
Квадратные уравнения и неравенства, содержащие параметры. 7ч
Свойства квадратичной функции в задачах с параметрами. 4ч
Рациональные уравнения. 2ч
Рациональные неравенства. 2 ч
Иррациональные уравнения. 2ч
Иррациональные неравенства. 2ч
Показательные и логарифмические уравнения, содержащие параметры. 4 ч
Показательные и логарифмические неравенства, содержащие параметры . 4ч
Производная и ее применения. 4ч
Тригонометрия и параметры. 4ч
Графические приемы решения. 4ч
Нестандартные задачи с параметрами. 6ч
количество решений уравнений;
уравнения и неравенства с параметрами с некоторыми условиями.
Текстовые задачи с использованием параметра. 4 ч
Слайд 10
Первоначальные сведения.
Определение параметра. Виды уравнений и неравенств, содержащих
параметр.
Основные приемы решения задач с параметрами.
Решение простейших уравнений с
параметрами.
Цель: Дать первоначальное представление учащимся о параметре; помочь привыкнуть к параметру, к необычной форме ответов при решении уравнений.
Слайд 11
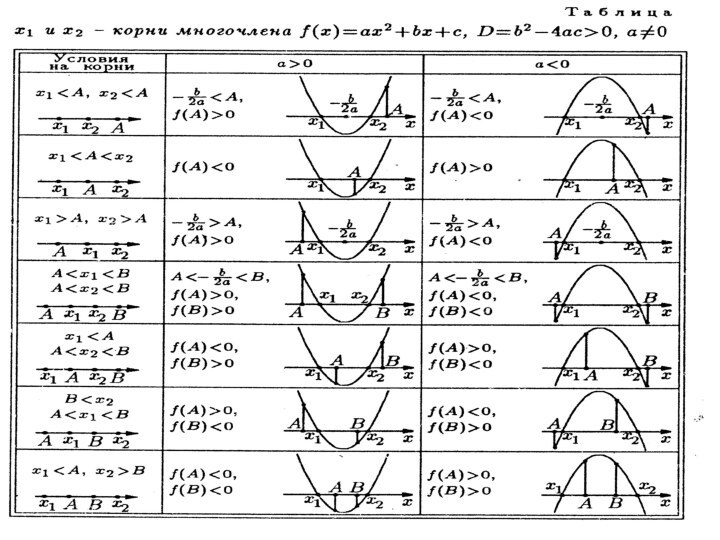
VI. Свойства квадратичной функции в задачах с параметрами.
Область
значений функции.
Область определения функции.
Монотонность. Координаты вершины параболы.
Цель: Познакомить с
многообразием задач с параметрами, решаемых с помощью свойств квадратичной функции.
Слайд 14
Методические рекомендации
при изучении некоторых тем
Слайд 15
Свойства квадратичной функции
в задачах с параметрами
Слайд 17
Введение элективного курса «Решение задач с
параметрами» необходимо учащимся в наше время как при подготовке
к ЕГЭ, так и к вступительным экзаменам в ВУЗы. Владение приемами решения задач с параметрами можно считать критерием знаний основных разделов школьной математики.
Слайд 18
При решении задач с
параметрами одновременно активно реализуются основные методические принципы:
Слайд 19
принцип параллельности – следует
постоянно держать в поле зрения несколько тем, постепенно продвигаясь
по ним вперед и вглубь;
Слайд 20
принцип вариативности – рассматриваются различные приемы и методы
решения с различных точек зрения: стандартность и оригинальность, объем
вычислительной и исследовательской работы;
Слайд 21
принцип самоконтроля – невозможность
подстроиться под ответ вынуждает делать регулярный и систематический анализ
своих ошибок и неудач;
Слайд 22
принцип регулярности – увлеченные математикой дети
с удовольствием дома индивидуально исследуют задачи, т. е. занятия
математикой становятся регулярными, а не от случая к случаю на уроках.