- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Элементы статистики 8 класс
Содержание
- 2. Цель проекта:
- 3. Определение статистики Статистика- это
- 4. Происхождение слова Слово «статистика» происходит от латинского слова status, которое означает «состояние, положение вещей».
- 5. Что изучает статистика? 1. Численность
- 6. Результаты статистических исследованийиспользуютсяПрактические выводыНаучные выводы
- 7. Начало статистического исследованияВсякое статистическое исследование начинается с
- 8. Продолжение статистического исследования Для обобщения и
- 9. Пример №1
- 10. Таблица частот
- 11. Анализ данных Для анализа статистических данных используют различные обобщающие показатели- статистические характеристики:1.Среднее арифметическое;2.Мода;3.Медиана;4.Размах.
- 12. Анализ результатов теста Средним арифметическим
- 13. Анализ результатов теста При анализе
- 14. Анализ результатов теста Наибольшее число
- 15. Анализ результатов теста Медианой(от лат.mediana, означ. «среднее»)
- 16. Анализ результатов теста Кроме таблицы
- 17. Наглядное представление статистической информации
- 18. Наглядное представление данных по результатам статистического исследования Построим круговую диаграмму
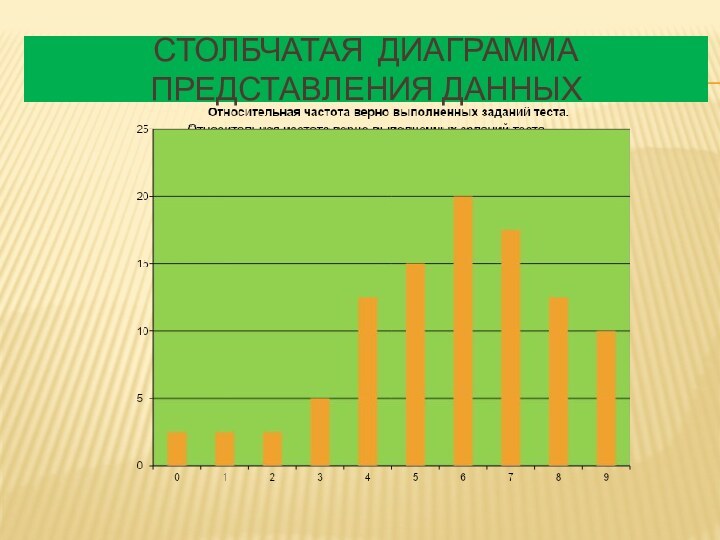
- 19. Столбчатая диаграмма представления данных
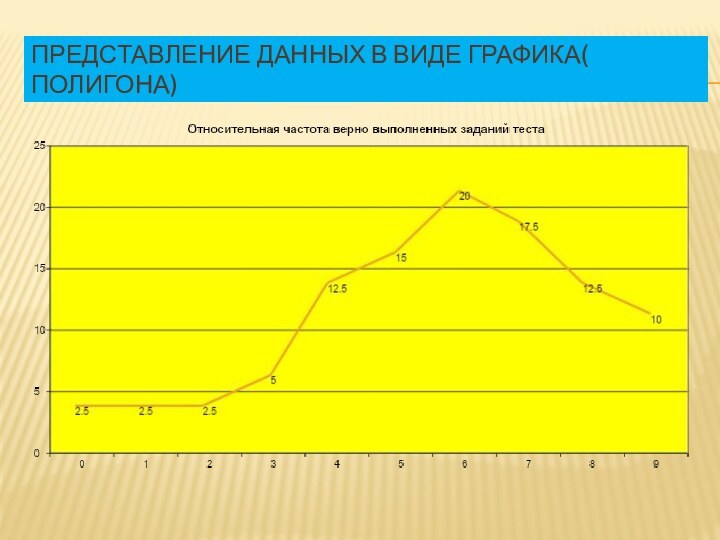
- 20. Представление данных в виде графика( полигона)
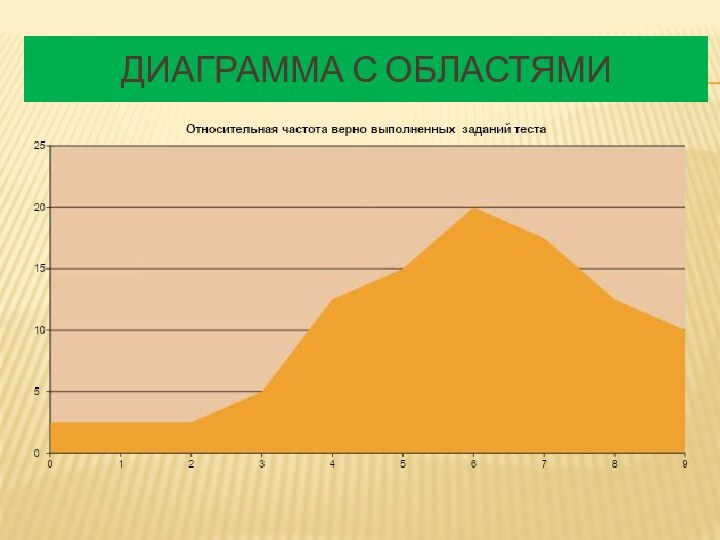
- 21. Диаграмма с областями
- 22. Построение полигона Динамику изменения статистических
- 23. Пример №2 Построим полигон по следующим
- 24. Интервальный ряд и работа с ним
- 25. ТАБЛИЦА исследования
- 26. Средняя продолжительность горения Пользуясь составленной
- 27. Получение ряда данных и изображениеДля получения ряда
- 28. Особенности массового исследования1.Большие организационные усилия;2.Большие финансовые затраты.Н.п.Перепись
- 29. Статистические методы обработки информацииТермины, принятые в статистике
- 30. Пример №3
- 31. Пример № 4
- 32. Дальнейшая обработка информацииСоставим таблицу распределения выборки:
- 33. Дальнейшая обработка информации
- 34. Практикум по решению задачЗадача 1028
- 35. Практикум по решению задачЗадача№1029
- 36. Практикум по решению задачЗадача№1030 Общее количество
- 37. Практикум по решению задачЗадача№1031. Наибольшее различие в
- 38. Решение задачЗадача №1034 Найдём
- 39. Скачать презентацию
- 40. Похожие презентации
Цель проекта: Обобщить знания по теме «Элементы статистики»,решать задачи по теме. («Алгебра» 7,8 класс, под редакцией С.А.Теляковского)































Слайд 2
Цель проекта:
Обобщить знания по теме «Элементы статистики»,решать задачи по теме.
(«Алгебра» 7,8 класс, под редакцией С.А.Теляковского)
Слайд 3
Определение статистики
Статистика- это наука,
которая занимается получением , обработкой и анализом количественных данных
о разнообразных массовых явлениях, происходящих в природе и обществе.
Слайд 4
Происхождение слова
Слово «статистика» происходит от
латинского слова status, которое означает «состояние, положение вещей».
Слайд 5
Что изучает статистика?
1. Численность отдельных
групп населения страны и её регионов;
2. Производство
и потребление разнообразных видов продукции; 3.Перевозку грузов и пассажиров различными видами транспорта; 4.Природные ресурсы и т.п.
Слайд 7
Начало статистического исследования
Всякое статистическое исследование начинается с целенаправленного
сбора информации об изучаемом явлении или процессе. Этот этап
называется этапом статистического наблюдения.
Слайд 8
Продолжение статистического исследования
Для обобщения и систематизации
данных, полученных в результате наблюдения, их по какому- либо
признаку разбивают на группы и результаты группировки сводят в таблицы.
Слайд 9
Пример №1
Администрация
школы решила проверить математическую подготовку восьмиклассников. С этой целью
был составлен тест, содержащий 9 заданий. Работу выполняли 40 учащихся школы. При проверке каждой работы отмечали число верно выполненных заданий.В результате был составлен такой ряд чисел:6,5,4,0,4,5,7,9,1,6,8,7,9,5,8,6,7,2,5,7,6,3,4,4,5,6,8,6,7,7,4,3,5,9,6,7,8,6,9,8
Для того чтобы удобно было анализировать полученные данные, упорядочим ряд:
0,1,2,3,3,4,4,4,4,4,5,5,5,5,5,5,6,6,6,6,6,6,6,6,7,7,7,7,7,7,7,8,8,8,8,8,9,9,9,9.
0.1.2.3.4,5,6,7,9- общий ряд данных
Представим полученные данные в виде таблицы, в которой для каждого числа верно выполненных заданий, записанных в верхней строке, укажем в нижней строке количество появлений этого числа в ряду, т.е.
ЧАСТОТУ
Слайд 11
Анализ данных
Для анализа статистических данных
используют различные обобщающие показатели- статистические характеристики:
1.Среднее арифметическое;
2.Мода;
3.Медиана;
4.Размах.
Слайд 12
Анализ результатов теста
Средним арифметическим ряда
чисел называется частное от деления суммы этих чисел на
число слагаемых.Найдём среднее арифметическое, используя таблицу частот. Надо общее число выполненных заданий разделить на число учащихся, т.е. на 40
0*1+1*2+2*1+3*2+4*5+5*6+6*8+7*7+8*5+9*4 = 232 = 5,8
40 40
Слайд 13
Анализ результатов теста
При анализе данных
интересно знать, какое количество верно выполненных заданий является типичным.
Модой ряда чисел называется число, которое встречается в данном ряду чаще других.Чаще встречаются работы, в которых верно выполнено 6 заданий.
6- мода ряда.
Слайд 14
Анализ результатов теста
Наибольшее число верно
выполненных учащимися заданий равно 9, а наименьшее равно 0.
Значит, размах рассматриваемого ряда данных равен9-0=9.
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Слайд 15
Анализ результатов теста
Медианой(от лат.mediana, означ. «среднее») называется
срединное число упорядоченного ряда.
Т.к в ряду 40
чисел, то медиана равна среднему арифметическому 20-го и 21-го членов ряда.Найдём, в какие группы попадают эти члены. Будем суммировать последовательно частоты и сравнивать суммы с числами 20 и 21.1+1+1+2+5+6=16, 1+1+1+1+2+5+6+8=24, т.е 20-й и 21-й члены попадают в ту группу, которую составляют учащиеся, верно выполнившие 6 заданий. Значит медиана ряда равна
( 6+6)/ 2=6.
Слайд 16
Анализ результатов теста
Кроме таблицы частот,
составляют таблицу , в которой указывается не частота, а
отношение частоты к общему числу данных в ряду. Это отношение, выраженное в процентах, называют относительной частотой, а саму таблицу- таблицей относительных частот.
Слайд 17
Наглядное представление статистической информации
Для
наглядного представления данных статистического исследования применяют различные способы их
изображения:1. Построение столбчатой диаграммы;
2. Построение круговой диаграммы;
3 Построение полигона;
4. Построение гистограммы;
5. Построение других видов диаграмм.
Слайд 18
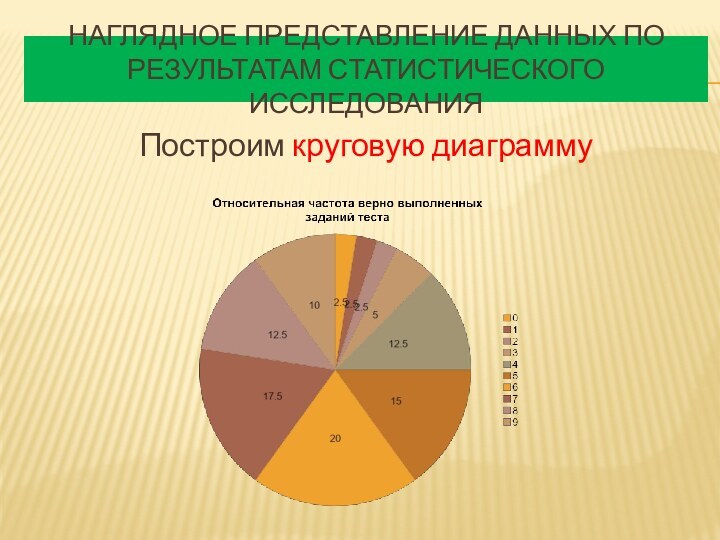
Наглядное представление данных по результатам статистического исследования
Построим
круговую диаграмму
Слайд 22
Построение полигона
Динамику изменения статистических данных
во времени часто иллюстрируют с помощью полигона (графика). Для
построения полигона отмечают в координатной плоскости точки, абсциссами которых служат моменты времени, а ординатами- соответствующие им статистические данные. Соединив точки отрезками, получим ломаную,которая называется полигоном(polygon- многоугольник).
Слайд 23
Пример №2
Построим полигон по следующим данным.
Имеются следующие данные о производстве
заводом приборов в первом полугодии 2012г. ( по месяцам)
Слайд 24
Интервальный ряд и работа с ним
В исследуемом ряду имеется большое число данных и
одинаковые значения встречаются редко. Для анализа данных строят интервальный ряд. Для этого разность между наибольшим и наименьшим значениями делят на несколько равных частей (примерно 5-10) и, округляя полученный результат, определяют длину интервала. За начало первого интервала часто берут наименьшее данное или ближайшее целое число , его не превосходящее.для каждого интервала указывают число данных, попадающих в этот интервал, или выраженное в процентах отношение этого числа к общей численности данных При этом граничное число обычно считают относящимся к последующему интервалу.ПРИМЕР. Пусть например, на партии из50 электроламп изучали продолжительность их горения (в часах). Составили таблицу
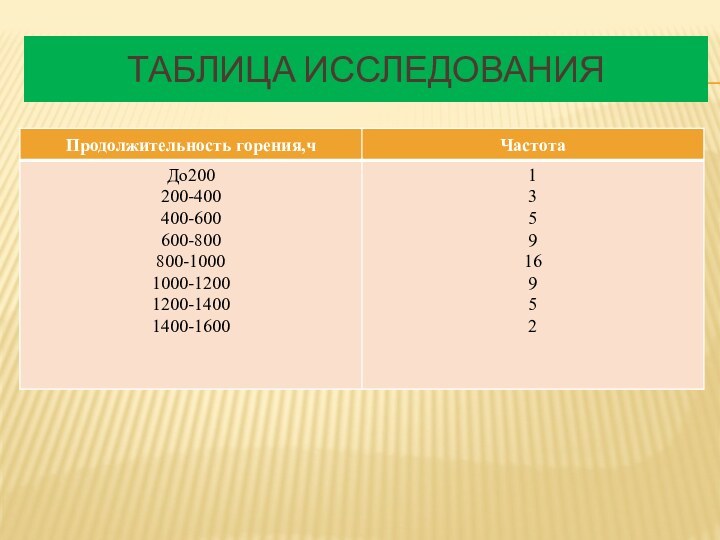
Слайд 26
Средняя продолжительность горения
Пользуясь составленной таблицей,
найдём среднюю продолжительность горения. Для этого составим новую таблицу
частот, заменяя каждый интервал числом, которое является его серединой
Слайд 27
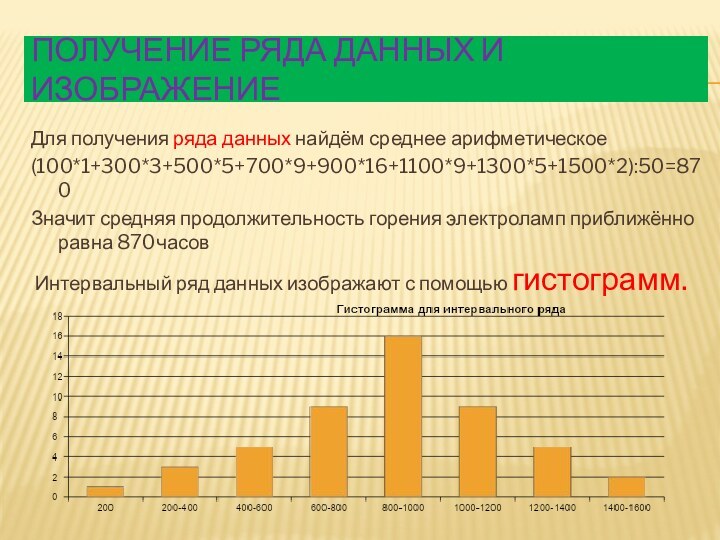
Получение ряда данных и изображение
Для получения ряда данных
найдём среднее арифметическое
(100*1+300*3+500*5+700*9+900*16+1100*9+1300*5+1500*2):50=870
Значит средняя продолжительность горения электроламп приближённо равна
870часовИнтервальный ряд данных изображают с помощью гистограмм.
Слайд 28
Особенности массового исследования
1.Большие организационные усилия;
2.Большие финансовые затраты.
Н.п.Перепись населения
страны связана с подготовкой разнообразной документации, выделением и инструктажём
переписчиков, сбором информации, обработкой собранных сведений.В тех случаях когда бывает сложно или даже невозможно провести сплошное исследование, его заменяют выборочным. При выборочном исследовании из всей изучаемой совокупности данных, называемой генеральной совокупностью выбирается определённая её часть, т.е.составляется выборочная совокупность(выборка)
Выборка должна быть представительной или репрезентативной.
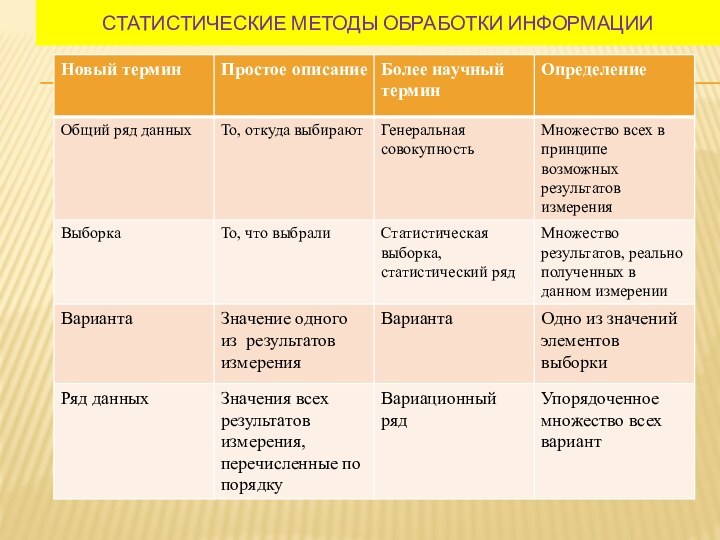
Слайд 30
Пример №3
Допустим, вы записываете номера месяцев рождения своих
одноклассников. В таком случае общий ряд данных- это числа от1 до 12, варианты- это номера месяцев рождения конкретных учеников именно вашего класса, а ряд данных - это все варианты , перечисленные по порядку. В одном классе ряд данных -это 3,4,5,7,8,10,11.В другом классе может получиться другой ряд данных. Например, 1,2,5,6,8,9,11,12 и т.д.
Слайд 31
Пример № 4
30 абитуриентов на четырёх вступительных экзаменах набрали
в сумме такие количества баллов (оценки на экзаменах выставлялись по пятибалльной системе):20,19,12.13,16,17,15,14,16,20,15,19,20,20,15,13,19,14,18,17,12,14,12,17,18,17,20,17,16,17. Составьте общий ряд данных, выборку из результатов, стоящих на чётных местах и соответствующий ряд данных.РешениеПосле получения двойки дальнейшие экзамены не сдаются, поэтому сумма баллов не может быть меньше 12.Значит, общий ряд данных состоит из чисел 12,13,14,15,16,17,18,19,20. выборка состоит из 15 результатов:19,13,17,14,20,19,20,…расположеннных на чётных местах. Ряд данных- это конечная возрастающая последовательность13,14,17,19,20.
Слайд 33
Дальнейшая обработка информации
кратность варианты
Частота варианты=----------------------------------
объём выборки
Составим таблицу распределения частот выборки:
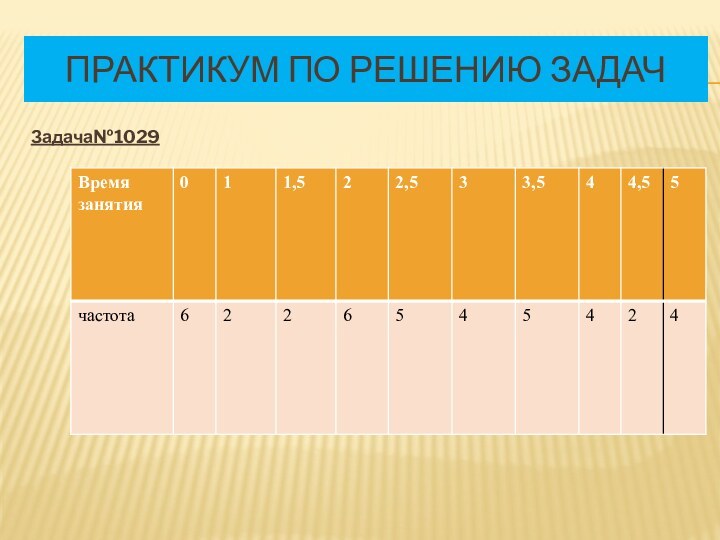
Слайд 36
Практикум по решению задач
Задача№1030 Общее количество учащихся
равно
27+53+87+223+146+89= 625.Вычислим количество процентов, которое составляет каждая группа учащихся:
27:625*100=4%,53:625*100=8%,87:625*100=14%,223:625*100=36%,
146:625*100=23%,89:625*100=14%(с
точностью до1%)Построим таблицу относительных частот
Слайд 37
Практикум по решению задач
Задача№1031. Наибольшее различие в числе
допущенных ошибок- это размах ряда. Он равен 6-0=6.Число ошибок,
являющееся типичным – это мода ряда. Мода равна 3.Задача№1032. Найдём среднее арифметическое ряда (2*20+5*12+10*7+25*4+100*2):45=470:45=10
2.Найдём размах ряда.100-2=88
3. Мода ряда-2
Задача№1033. Найдём среднее арифметическое ряда
(8*0+1*22+2*13+3*5+4*2):50=71:50=1,4 =1
Найдём размах ряда4-0=4
Найдём моду ряда-1
Слайд 38
Решение задач
Задача №1034 Найдём среднее
арифметическое ряда
(0*3+1*16+2*26+3*17+4*18+5*10+6*3+7*5+8*1+9*1) :100=311:100=3
Мода ряда-2
Задача№1036 Середина 1 интервала-13,5,середина
2 интервала16,5, середина 3 интервала-19,5. Найдём среднее арифметическое ряда(13,5*4+16,5*6+19,5*3) :13 =16,2=16
Ответ: каждый завод региона в среднем перерабатывал в сутки 16тыс.ц сахара
Задача №1037 а)-нет, б)-да, в)- нет
Задача№1038 думаем!





























