Презентация на тему Квадратичні нерівності

Міні-підручник

“Квадратичні нерівності”

Задачі і вправи
§5. Завдання для самостійної роботи
§6. Відпочинь з

користю
§7. Твори бо ти здібний!
§8. З математикою по життю.

частина якої є вираз___, де a ___, b, c

– дані числа і x – змінна, а права - ____. Нерівності в яких знак є >, < називаються строгими та ____, якщо знак ≥, ≤. Під час розв’язання строгих, не строгих нерівностей на числовому промені точки позначають ____ та ____. Для розв’язання квадратних нерівностей використовують графік квадратичної функцій - ____. Напрям віток параболи визначається ____, якщо вітки направлені вгору, то a ____, та якщо вітки направлені ____ то а < 0. при розв’язуванні квадратних нерівностей використовуються формули знаходження дискримінанта D=____ та коренів рівняння х1=____ х2=____ або за теоремою Вієта х1 + х2 =____, х1*х2=____.

користуватися перетворенням графіків квадратичної функції.

§2. Усні вправи

Воно було введено у 17 столітті, коли у зв'язку

з розвитком механіки
у математику проникли ідеї зміни і руху.

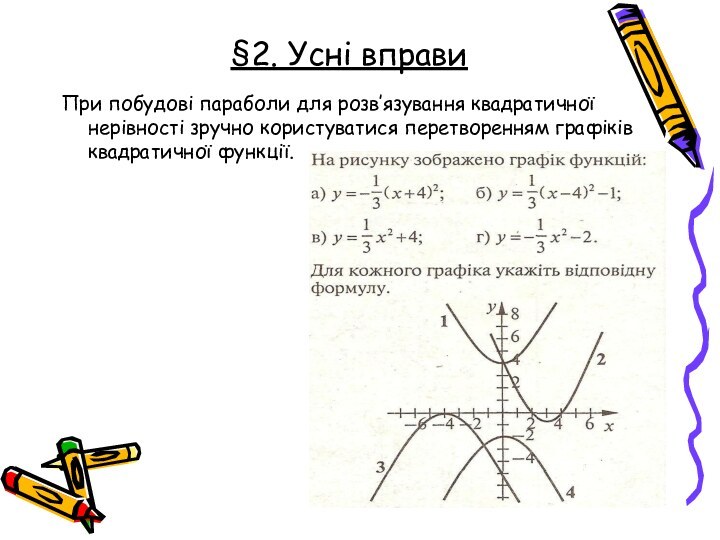
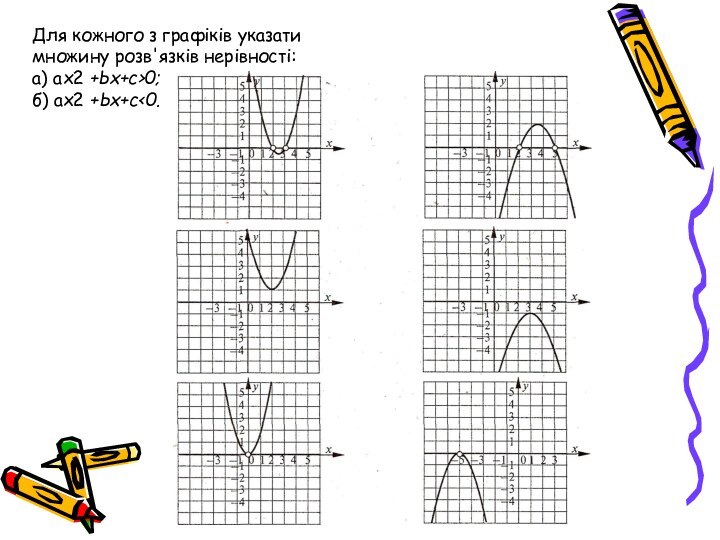
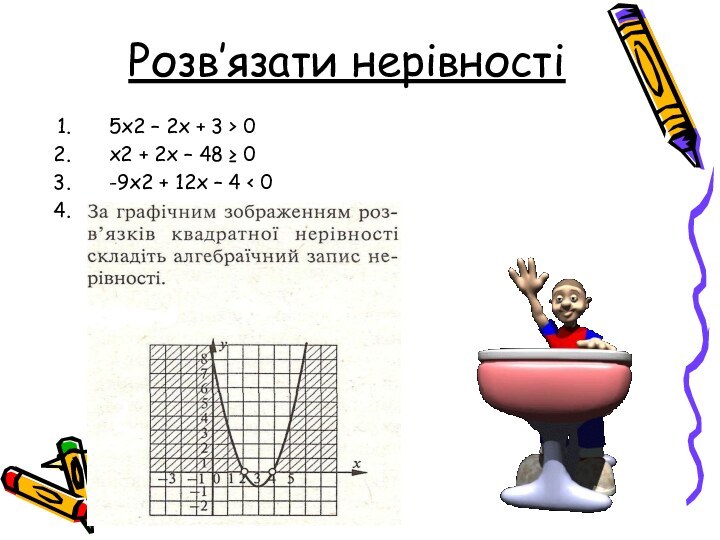
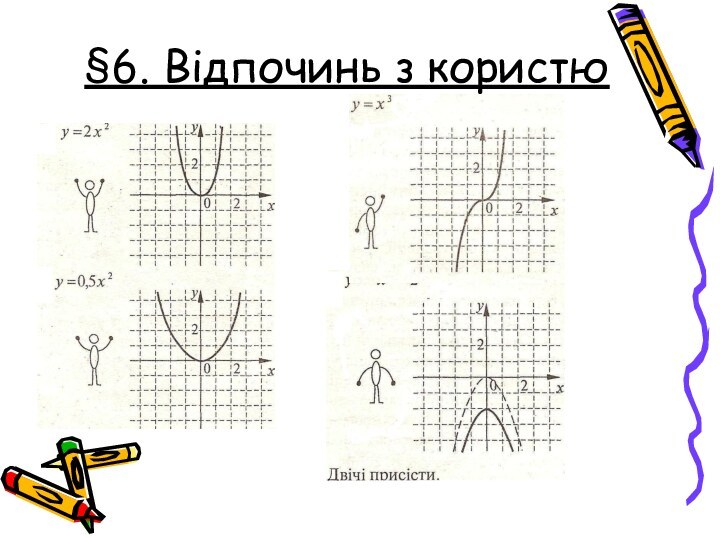
Французькі математики П'єр Ферма (1601-1665)
та Рене Декарт (1596-1650) розглядали функцію як залежність ординати точки кривої від її абсциси.

Термін «функція» (від латинського functio — виконання, звершення)
для назви залежностей вперше ввів Готфрід Лейбніц (1646-1716).
Він пов'язував функцію з графіками.

учень Леонард Ейлер (1707-1783)
розглядали функцію як аналітичний вираз,

тобто вираз,
утворений із змінних чисел за допомогою
тих чи інших аналітичних операцій.

Найзагальніше сучасне означення поняття «функція» запропонувала в середині
XX ст. група математиків, яка виступила під псевдонімом Нікола Бурбакі.

Функцію як залежність однієї змінної величини від іншої ввів
чеський математик Бернард Больцано (1781-1848).

ах2 +Ьх+с>0;
б) ах2 +Ьх+с

+ с>< 0.

1) Визначаємо напрямок віток параболи, яка відповідає

функції у = ах2 + Ьх + с.
2) Знаходимо розв'язки квадратного тричлена
ах2 + Ьх + с (розв'язуємо рівняння ах2 +Ьх + с=0).
3) Будуємо ескіз графіка функції у = ах2 + Ьх + с
4) Вибираємо значення змінної, які відповідають розв'язкам нерівності.
5) Записуємо відповідь.

у = f (х).
2) Знайти нулі

функції у = f (х) (f (х) = 0)
3) Нанести нулі на область визначення.
4) Визначити знаки функції f (х) в кожному інтервалі, на які розбивається область визначення нулями функції.
5) Записати відповідь.

за поданою карткою-підказкою.


Картка-підказка
1) Знайдемо нулі функції у = (х-5)(х+7)(х+9):
Х1

=________; Х2 =________; Х3 =________•
2) Позначимо на координатній прямій нулі функції:
х
3) Знайдемо знаки цієї функції в кожному із здобутих проміжків, скориставшись властивістю чергування знаків.
4) 3 рисунка бачимо, що множиною розв'язків нерівності є об'єднання проміжків.
Відповідь.__________________________

+ 2x – 48 ≥ 0
-9x2 + 12x –

4 < 0

прислів'я
Наприклад

рукою, не лінуйся, а учись,
Бо, чого навчишся в школі,

знадобиться ще в житті колись