Презентация на тему Формула объёма шара

знания по теме «Тела вращения»
Ход урока:
I. Организационный момент.

II. Актуализация опорных знаний.
Устная работа
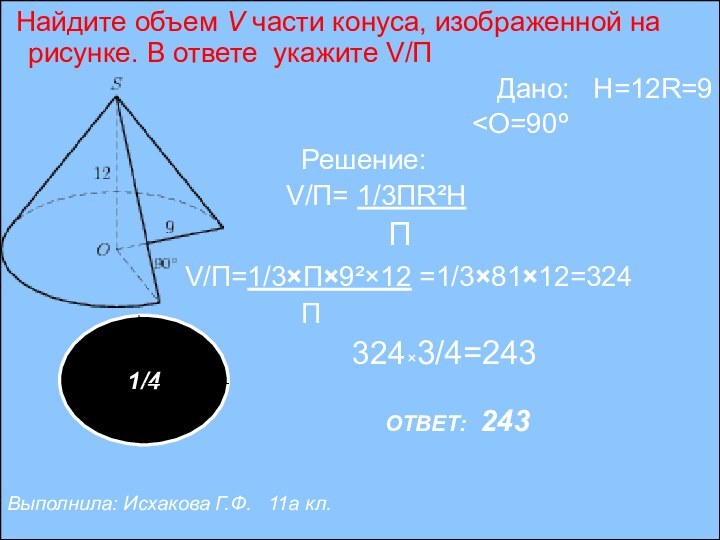
2) Презентации решений задач с ЕГЭ
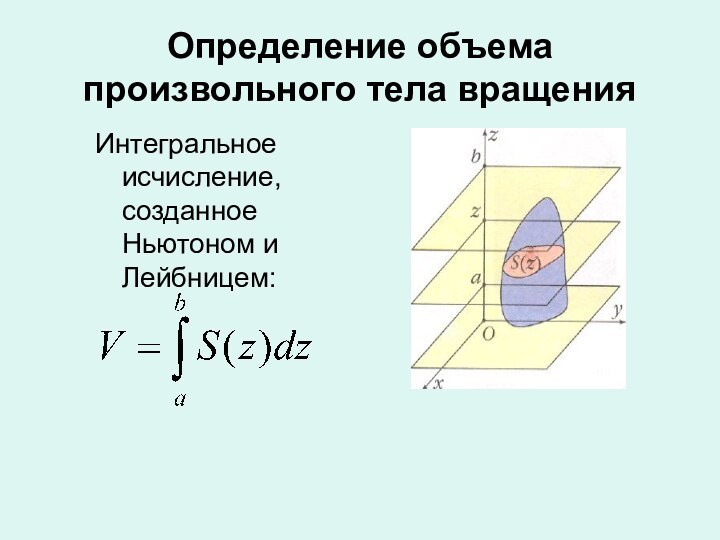
III. Изучение новой темы
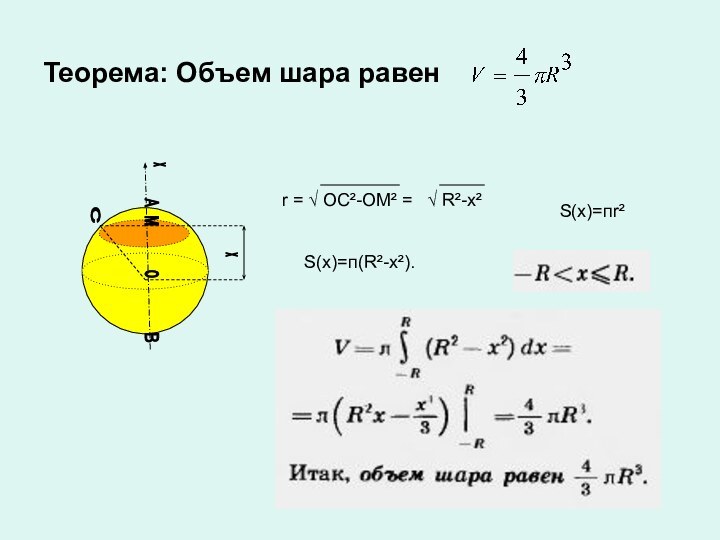
Теорема
IV.Формирование умений и навыков учащихся.
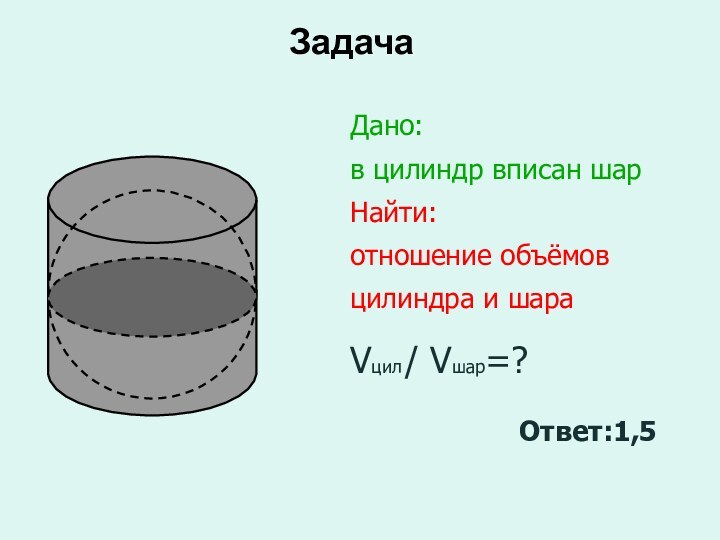
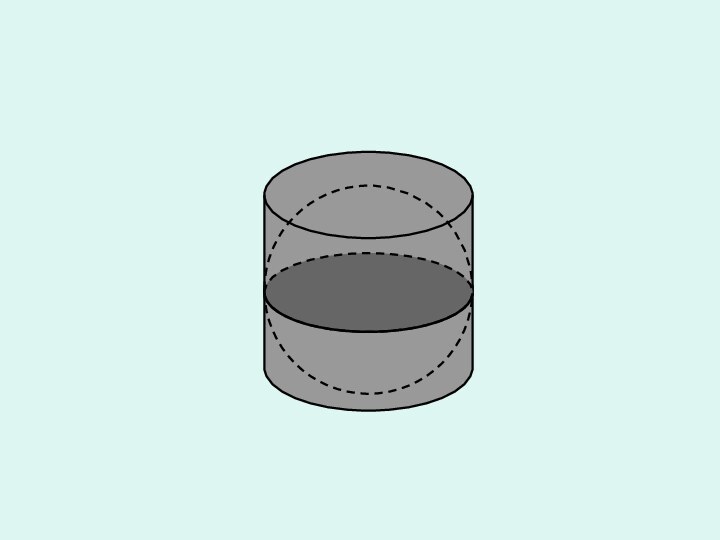
Проблемная задача
Задача Архимеда
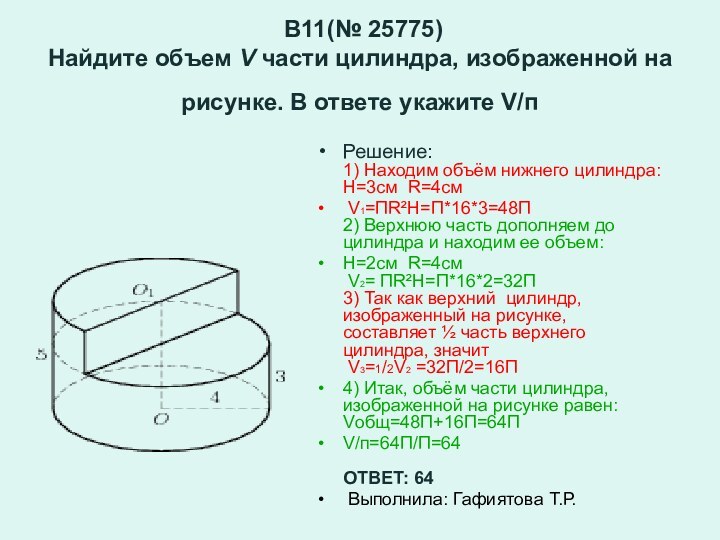
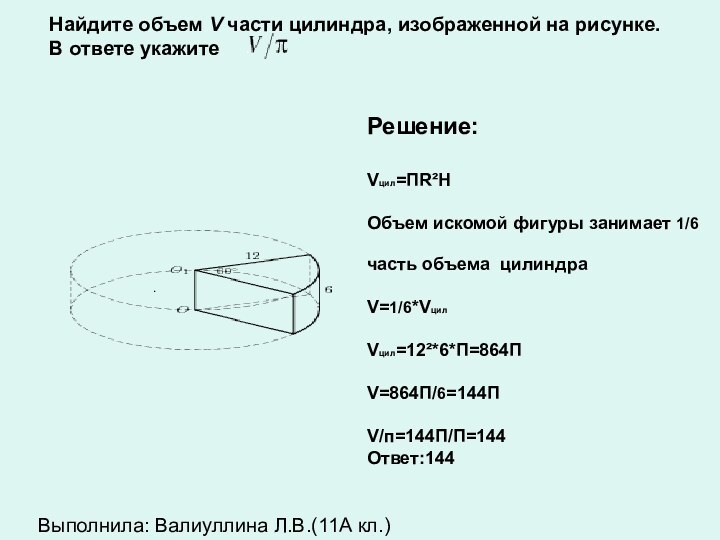
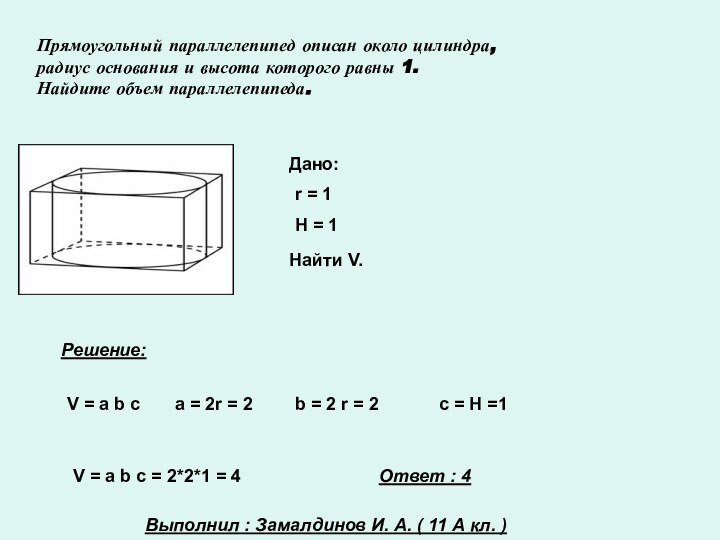
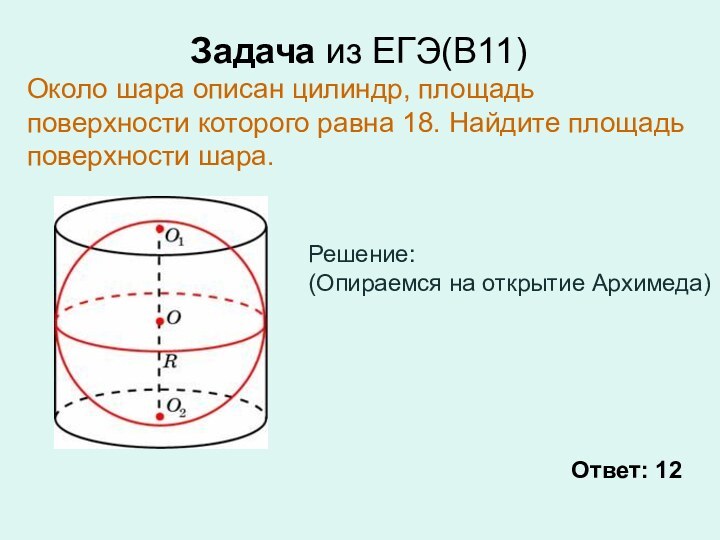
Задачи из ЕГЭ(В9)
V. Итог урока. Домашнее задание.

площади поверхности тел.
1.Цилиндр 2.Конус 3.Усеченный конус 4. Шар

B11(№ 25775) Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/п

Решение: 1) Находим объём нижнего цилиндра: H=3см R=4см
V1=ПR²H=П*16*3=48П 2) Верхнюю часть дополняем до цилиндра и находим ее объем:
Н=2см R=4см V2= ПR²H=П*16*2=32П 3) Так как верхний цилиндр, изображенный на рисунке, составляет ½ часть верхнего цилиндра, значит V3=1/2V2 =32П/2=16П
4) Итак, объём части цилиндра, изображенной на рисунке равен: Vобщ=48П+16П=64П
V/п=64П/П=64 ОТВЕТ: 64
Выполнила: Гафиятова Т.Р.

Найдите объем V части цилиндра, изображенной на рисунке.
В ответе укажите

Выполнила: Валиуллина Л.В.(11А кл.)

высота которого равны 1.
Найдите объем параллелепипеда.
Дано:
r = 1
H

= 1

Найти V.

Решение:

V = a b c

a = 2r = 2

b = 2 r = 2

с = Н =1

V = a b c = 2*2*1 = 4

Ответ : 4

Выполнил : Замалдинов И. А. ( 11 А кл. )

рисунке. В ответе укажите V/П

Дано: H=12R=9
Решение:
V/П= 1/3ПR²H
П
V/П=1/3×П×9²×12 =1/3×81×12=324
П
324×3/4=243

ОТВЕТ: 243


Выполнила: Исхакова Г.Ф. 11а кл.

1/4

Найдите объем V части цилиндра, изображенной

на рисунке. В ответе укажите
R=3;H=4.
Решение:
Vц = π R²H=π·3²·4=36π.
Так как объем искомой фигуры занимает ¼ часть целого
цилиндра, ее объем будет равен: 36π/4=9π
По условию задачи объем искомой фигуры будет равен: 9π/π=9.
Ответ:9 Выполнила: Арсланова Л.И. (11А кл)

что
V=1350/5/6=1125

Решение:
.
Найдите объем V части цилиндра, изображенной
на рисунке.
В

ответе укажите

V/

Ответ:1125

Выполнила: Галиуллина М.Ф. (11Акл)

(шара)
A;F – полюсы сферы (шара)
ОВ – радиус сферы (шара)
BC

– диаметр сферы (шара)

О

А

R

C

F

Шар – множество точек пространства, находящихся на расстоянии не большем R от данной точки.
Фигура, полученная в результате вращения полукруга вокруг диаметра, называется шаром.

B

и Лейбницем:

= √ R²-x²
S(x)=пr²
S(x)=п(R²-x²).

Однако, выход был найден: арбуз диаметром 3 дм приравнивали

по стоимости к трём арбузам диаметром 1 дм.
Что вы возьмете?
Правы ли были продавцы?

=

+

+

шара
Vцил / Vшар=?

Ответ:1,5

меньше объема описанного около него цилиндра и что также

относятся поверхности этих тел.

которого равна 18. Найдите площадь поверхности шара.


Ответ: 12
Решение:
(Опираемся

на открытие Архимеда)

раз уменьшился объем шара?
Решение:
Пусть радиус первого шара R, уменьшенного

r.
Поверхность шара S1 = 4пR², стала
S2 = 4пR²/9 = 4п (R/3)² = 4пr²
Видим, что r =R/3, т.е. радиус уменьшился в 3 раза.

Объем V1= 4/3 ПR³, а объем V2= 4/3 пr³ =
=4/3 п(R/3)³ =4/3 пR³ /27 = V1 / 27

Ответ:27

Задача из ЕГЭ(В11)

712,
II уровень: №714
с презентацией.