без просвета:
с помощью одноимённых правильных многоугольников;
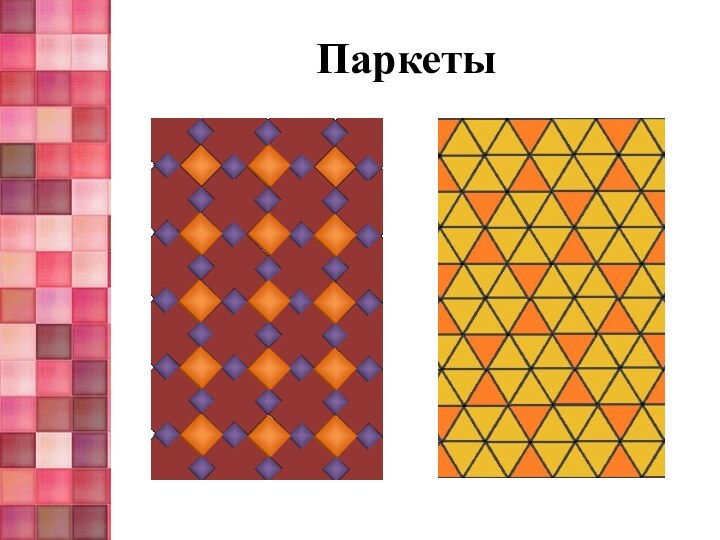
с помощью правильных многоугольников двух различных форм;
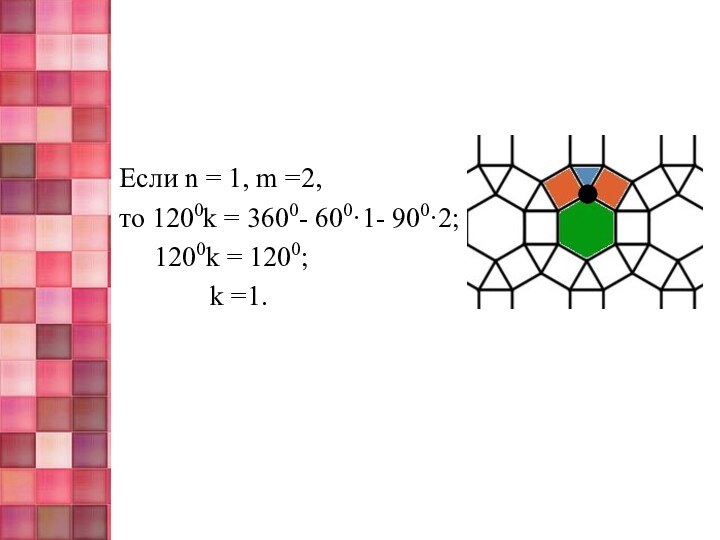
с помощью правильных многоугольников
трех различных форм.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть







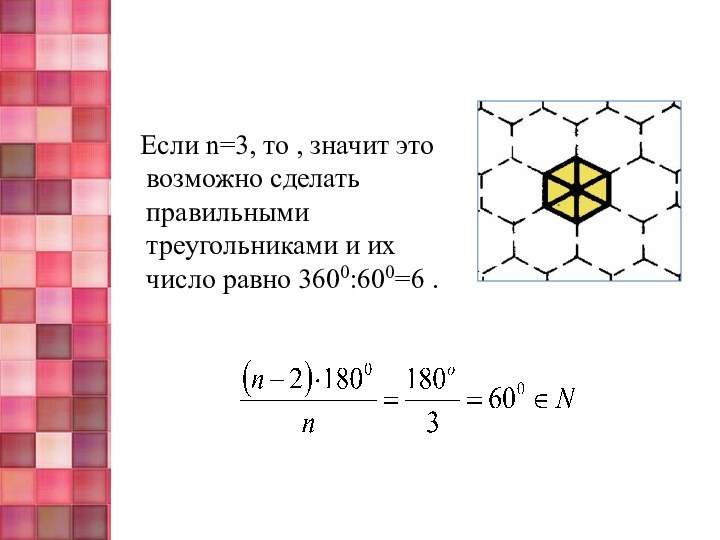
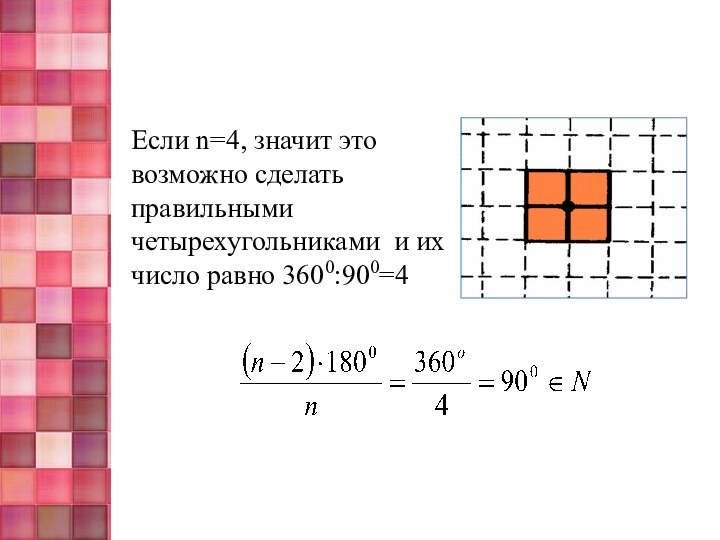



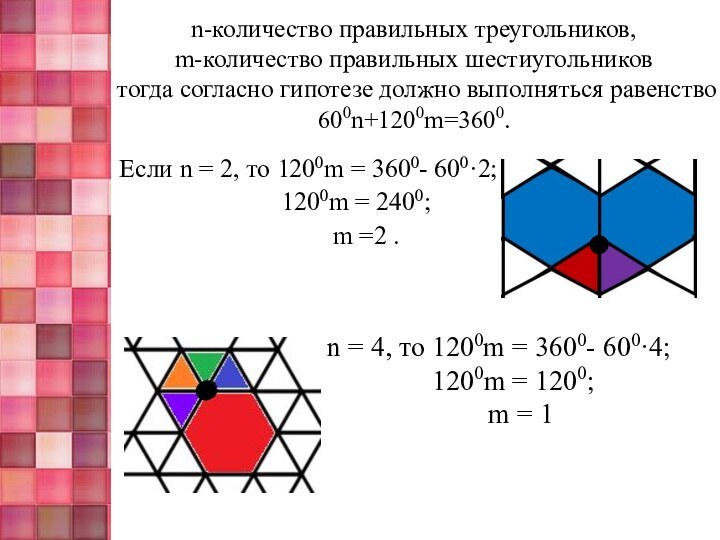







n = 4, то 1200m = 3600- 600·4;
1200m = 1200;
m = 1
Если n = 2, m =1,
то 1500k = 3600- 600·2-900·1;
1500k = 1500;
k =1.