- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
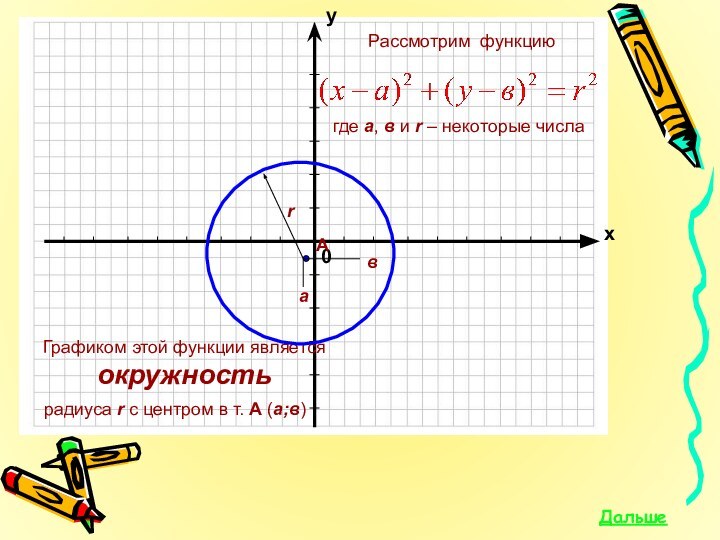
Презентация на тему графический способ решения систем уравнения
Содержание
- 2. Николай Егорович Жуковский сказал:«В математике есть своя красота, как в живописи и поэзии».
- 3. Воспитательные: - воспитание коллективизма и ответственности за
- 4. Вы, конечно, помните, что графиком функции называют
- 5. Графиком этой функции является прямая
- 6. График этой функции называется гиперболой
- 7. Дальше
- 8. Графиком этой функции является параболаДальше
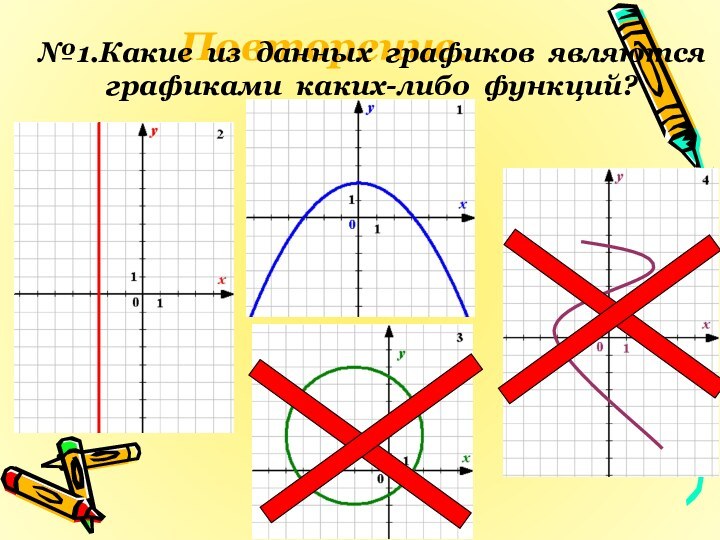
- 9. Повторение.№1.Какие из данных графиков являются графиками каких-либо функций?
- 10. № 2. Повторение.Линейные функции.y = ах + bВерно!
- 11. № 2. Повторение.Квадратичные функции.Молодцы!у = ах2 + bx +c
- 12. № 2. Повторение.Функции прямой пропорциональности.у = kxПравильно!
- 13. № 2. Повторение.Функции обратной пропорциональности.у = k/xИ все!
- 14. у = а y = kxy =
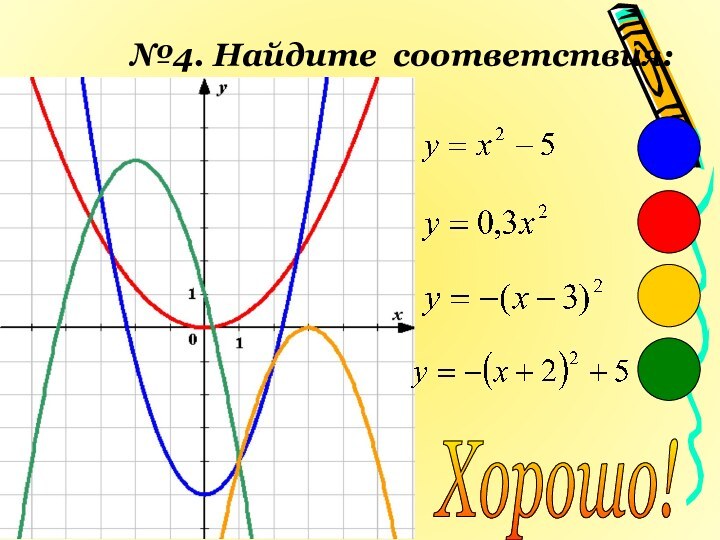
- 15. №4. Найдите соответствия:Хорошо!
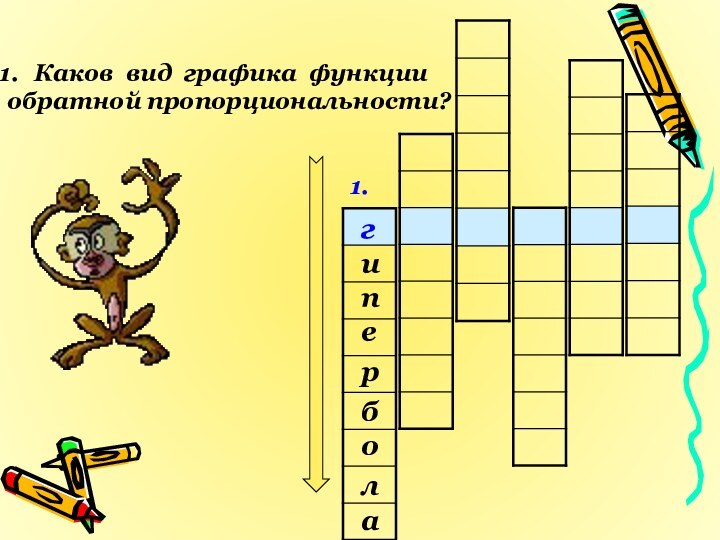
- 16. 1.гКаков вид графика функцииобратной пропорциональности? иепалобр
- 17. 1.2.ргиепалобрКаков вид графика квадратичной функции?пабалоа
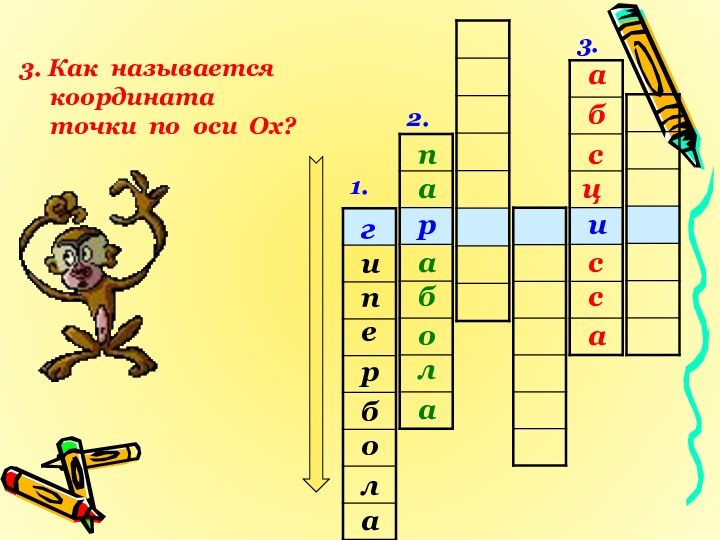
- 18. 1.2.3.иргиепалобр3. Как называется координата точки по оси Ох?пабалоабасцсас
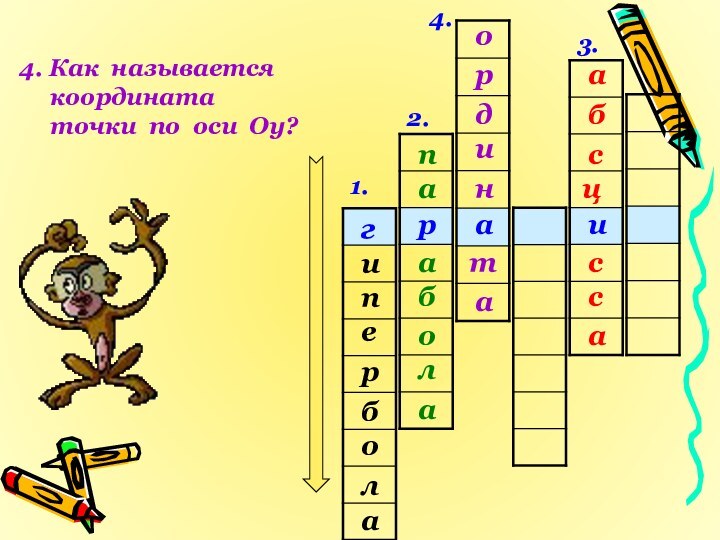
- 19. 1.2.3.4.иаргиепалобр4. Как называется координата точки по оси Оу?пабалоабасцсасронидат
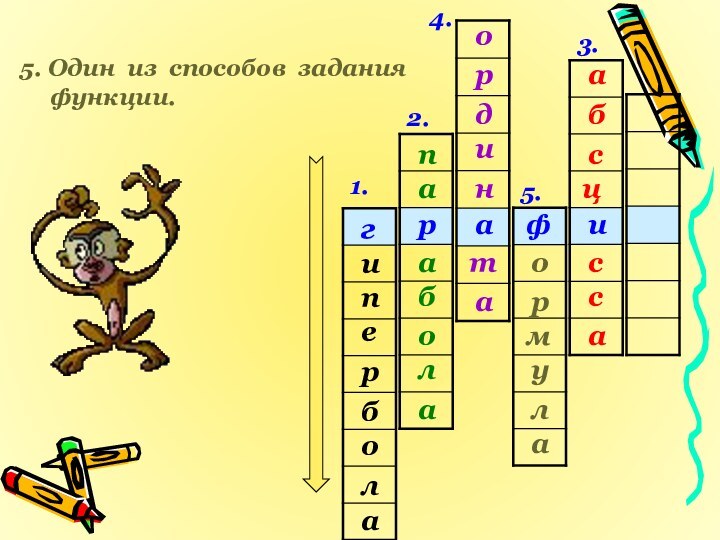
- 20. 1.2.3.4.5.ифаргиепалобр5. Один из способов задания функции. пабалоабасцсасронидатроалум
- 21. 1.2.3.4.5.6.ифаргиепалобр6. Переменная величина,значение которой зависитот изменения другойвеличины.пабалоабасцсасронидатроалумфуикнця
- 22. Итак, начнём…
- 23. Графический способ решения системы уравнений с
- 24. Графиком уравнений с двумя переменными может быть:Прямая Парабола ГиперболаОкружность…xx
- 25. Построим в одной системе координат графики уравненийх2
- 26. Давайте сделаем из рассмотренного примера выводы.Помните о
- 27. Тренировочные упражнения.Решить №418 из учебника.
- 28. ФИЗКУЛЬТМИНУТКА !
- 29. Подготовка к ГИА:- решить систему уравнений графическим
- 30. Проверка. Решить графически систему уравнений-Графиком первого
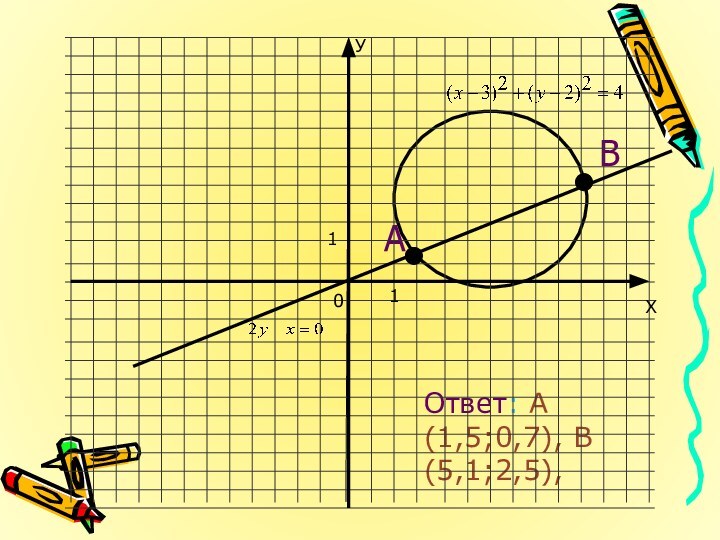
- 31. Ответ: А(1,5;0,7), В(5,1;2,5), 110ХУ
- 32. ТестированиеВам предлагается тест, состоящий из 5 вопросов.
- 33. 1. С какой прямой график параболы y=
- 34. 1322. Укажите систему уравнений, которая не имеет решений.4ОДНО решениеВЕРНО!ДВА решенияПОДУМАЙ!y=x2-1y-10=0x-y=3x+5=0Все три указанные системы
- 35. 3123. Укажите систему уравнений, решение которой пара
- 36. 312 4. На рисунке изображены графики
- 37. 321 5. На рисунке изображены графики
- 38. Домашнее задание: П. 18, №421(а), №422(б)
- 39. Итог урока: - С каким способом решения
- 40. Успехов!!!До новых встреч!
- 41. «Ученые, занимавшиеся понятием «Ученые, занимавшиеся понятием «Ученые, занимавшиеся понятием функция»
- 42. Идея функциональной зависимости восходит к древности. Ее
- 43. Введено было единое обозначение: неизвестных - последними
- 44. Само слово «функция» (от латинского functio -совершение,
- 45. Поговорим о русских ученых, внесших вклад в
- 46. Соболев Сергей Львович (род. в 1908г.) Это
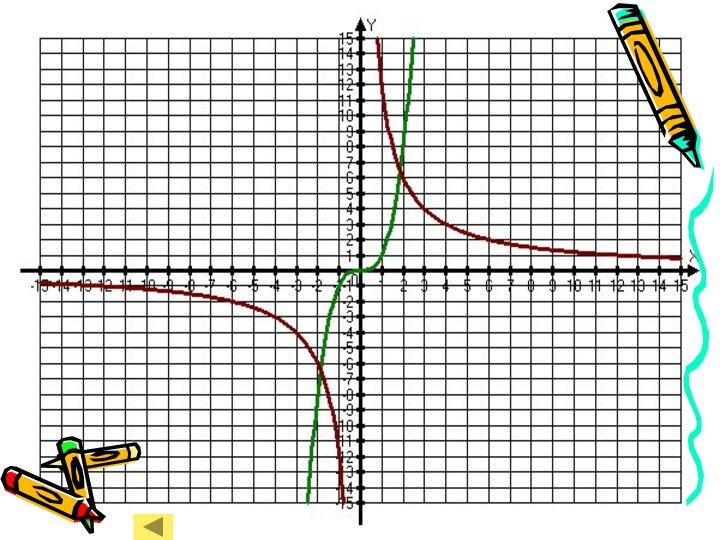
- 47. 1 заданиеРешите графически системы уравнений:ПроверьПроверь
- 48. Полученная система:
- 49. Полученная система:
- 52. 2 заданиеНа чертеже дан график одного из
- 53. Полученная система:
- 55. В данную систему впишите уравнение линии, изображенной
- 56. Полученная система:
- 58. Скачать презентацию
- 59. Похожие презентации




































Слайд 2
Николай Егорович Жуковский сказал:
«В математике есть своя красота,
как в живописи и поэзии».
Слайд 3
Воспитательные:
- воспитание коллективизма и ответственности за общую
работу;
- воспитание взаимопомощи;
-
воспитание аккуратности (при выполнении построения графиков функций).Развивающие:
- формировать умения сравнивать, обобщать изучаемые факты;
- развивать у учащихся самостоятельность в мышлении и учебной деятельности;
- повысить эмоциональный настрой учащихся путем привлечения наглядности и технических средств обучения (компьютер).
Образовательные:
- научиться применять полученные знания к построению графиков функций;
- сформировать умения решать системы уравнений графическим способом.
Цели урока:
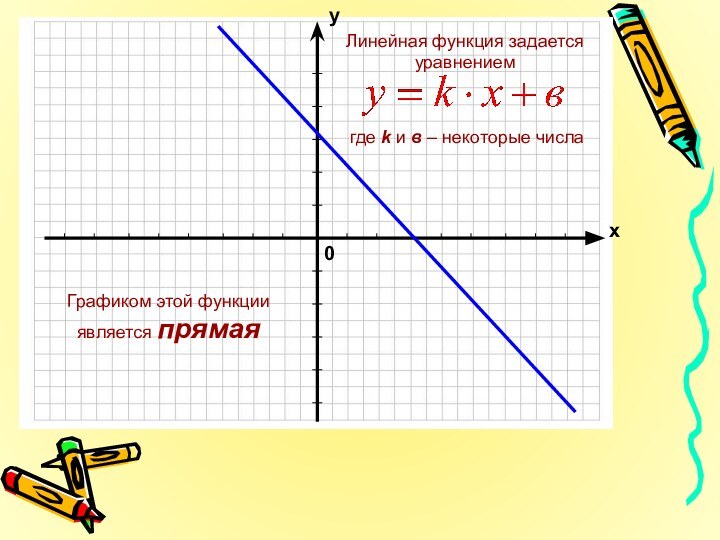
Слайд 4 Вы, конечно, помните, что графиком функции называют множество
всех точек координатной плоскости, абсциссы которых равны значениям аргументов,
а ординаты – соответствующим значениям функции.у = f(х)
Вы уже знакомы с некоторыми важными видами функций
Слайд 14
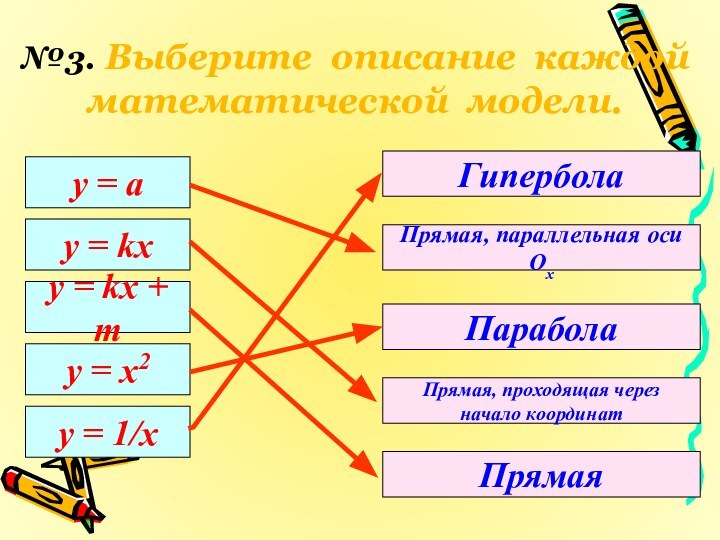
у = а
y = kx
y = kx
+ m
y = x2
y = 1/x
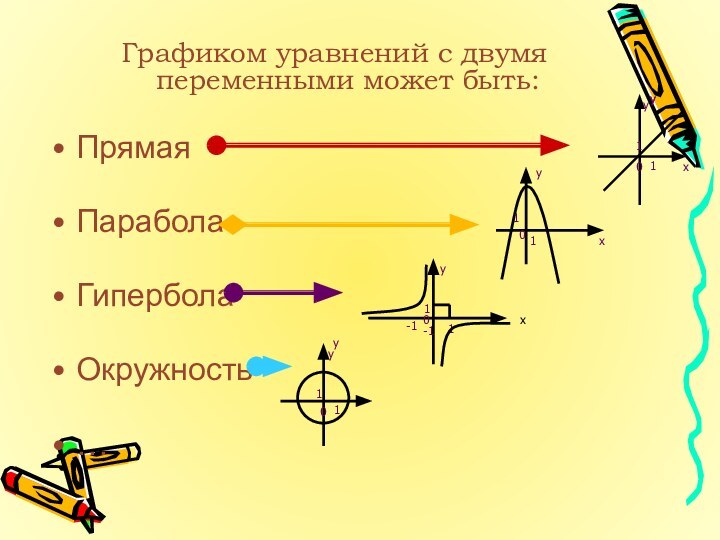
Прямая, параллельная оси Ох
Парабола
Гипербола
Прямая,
проходящая через начало координат
Прямая
№3. Выберите описание каждой
математической модели.
Слайд 21
1.
2.
3.
4.
5.
6.
и
ф
а
р
г
и
е
п
а
л
о
б
р
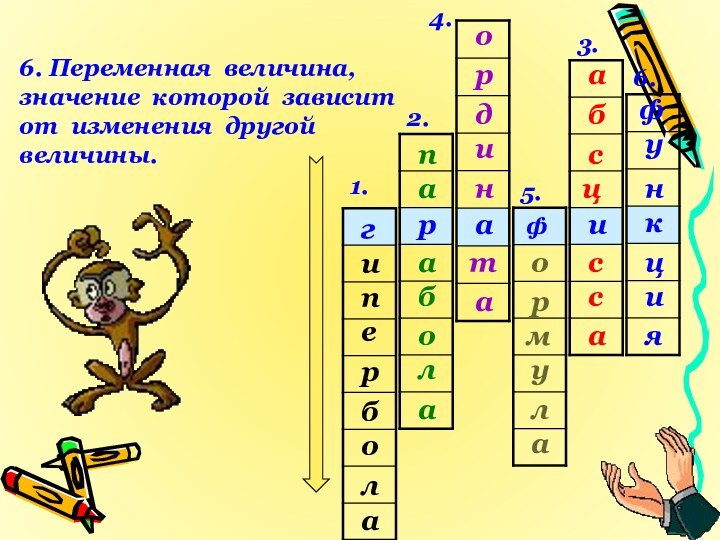
6. Переменная величина,
значение которой зависит
от изменения другой
величины.
п
а
б
а
л
о
а
б
а
с
ц
с
а
с
р
о
н
и
д
а
т
р
о
а
л
у
м
ф
у
и
к
н
ц
я
Слайд 23
Графический способ решения системы уравнений с двумя
переменными - один из самых простых и наглядных способов.
Но
этот способ напрямую связан с построением графиков уравнений, входящих в ту или иную систему.Итак…
Дальше
Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство
Слайд 25
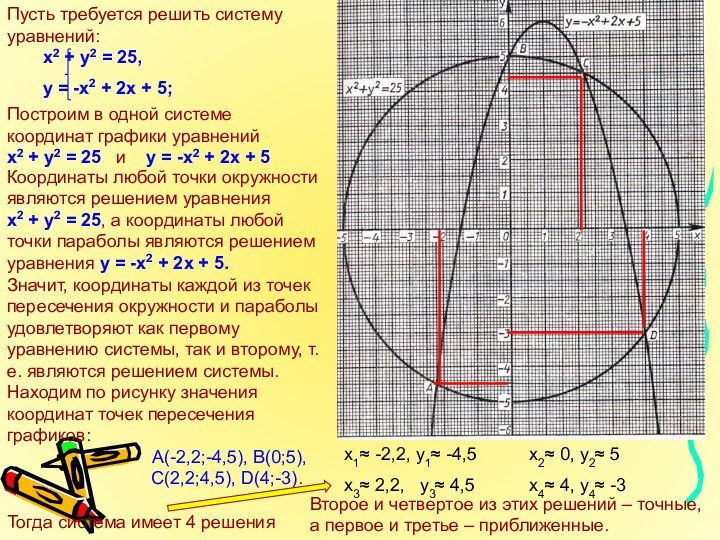
Построим в одной системе координат графики уравнений
х2 +
у2 = 25 и у = -х2
+ 2х + 5Координаты любой точки окружности являются решением уравнения х2 + у2 = 25, а координаты любой точки параболы являются решением уравнения у = -х2 + 2х + 5.
Значит, координаты каждой из точек пересечения окружности и параболы удовлетворяют как первому уравнению системы, так и второму, т.е. являются решением системы.
Находим по рисунку значения координат точек пересечения графиков:
А(-2,2;-4,5), В(0;5),
С(2,2;4,5), D(4;-3).
Тогда система имеет 4 решения
х1≈ -2,2, у1≈ -4,5 х2≈ 0, у2≈ 5
х3≈ 2,2, у3≈ 4,5 х4≈ 4, у4≈ -3
Второе и четвертое из этих решений – точные,
а первое и третье – приближенные.
Слайд 26
Давайте сделаем из рассмотренного примера выводы.
Помните о двух
вещах!
Если точек пересечения графиков нет, то система решений не
имеет;Координаты точек пересечения определяются приблизительно, поэтому и решения могут получиться приблизительными;
Чтобы проверить точность полученных решений, их нужно
подставить в уравнения системы!
Чтобы решить систему двух уравнений с двумя неизвестными, нужно:
Построить в одной системе координат графики уравнений, входящих в систему;
Определить координаты всех точек пересечений графиков (если они есть);
Координаты этих точек и будут решениями системы.
Слайд 29
Подготовка к ГИА:
- решить систему уравнений графическим способом
самостоятельно (из сборника заданий для подготовки к ГИА С.С.Минаева,
Т.В.Колесникова)
Слайд 30
Проверка. Решить графически систему уравнений
-Графиком первого уравнения
является окружность с центром в точке (3;2) и радиусом2.
-Графиком
второго уравнения является прямая проходящая через начало координат-Построим графики для каждого
из уравнений.
Слайд 32
Тестирование
Вам предлагается тест, состоящий из
5 вопросов.
Внимательно
прочитайте каждый вопрос и варианты ответов к ним.
Выберите
правильный вариант ответа.
Слайд 33
1. С какой прямой график параболы
y= –
x2+ 4x – 3 не имеет общих точек?
о
х
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
у
-1
-2
-3
-4
-5
-6
у = 0
у = x
у = 1
у = –10
7
6
5
4
3
2
1
Слайд 34
1
3
2
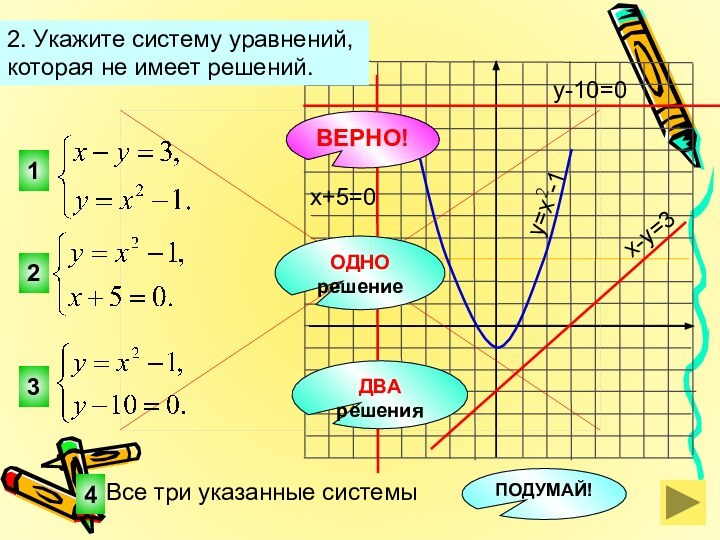
2. Укажите систему уравнений,
которая не имеет решений.
4
ОДНО
решение
ВЕРНО!
ДВА решения
ПОДУМАЙ!
y=x2-1
y-10=0
x-y=3
x+5=0
Все три указанные системы
Слайд 35
3
1
2
3. Укажите систему уравнений,
решение которой пара (4;0)
4
Решение
(-4; -5)!
ВЕРНО!
Решение (1; 4)!
ПОДУМАЙ!
7х-5у=-8
x-2y=4
x+у=4
Такой системы нет
1 2
3 4 5 6 7-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
Слайд 36
3
1
2
4. На рисунке изображены
графики функций
у=х2 – 2х–3 и у=1–х
Используя графики решите
систему уравнений.
4
ВЕРНО!
ПОДУМАЙ!
ПОДУМАЙ!
у=1–х
у=х2 – 2х –3
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
(-2; 5), (2; -3)
х1=-2 , х2=2;
ПОДУМАЙ!
Нет решений
у1=-3 , у2=5;
Слайд 37
3
2
1
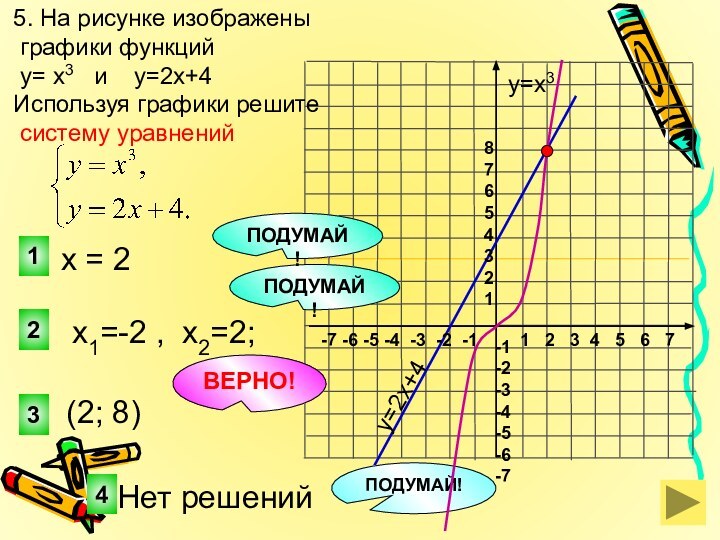
5. На рисунке изображены
графики функций
у= х3 и у=2х+4
Используя графики
решите систему уравнений
4
ПОДУМАЙ!
ПОДУМАЙ!
у=2х+4
у=х3
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
8
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
(2; 8)
х1=-2 , х2=2;
ПОДУМАЙ!
Нет решений
х = 2
ВЕРНО!
Слайд 39
Итог урока:
- С каким способом решения систем уравнений
с двумя переменными мы познакомились?
- В чем заключается его
суть?- Дает ли данный способ точные результаты?
- В каком случае система не будет иметь решений?
Слайд 41
«Ученые, занимавшиеся понятием «Ученые, занимавшиеся понятием
«Ученые, занимавшиеся понятием функция»
Слайд 42 Идея функциональной зависимости восходит к древности. Ее содержание
обнаруживается уже в первых математически выраженных соотношениях между величинами,
в первых правилах действий над числами.Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и
Рене Декарт.
Они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание.
Слайд 43 Введено было единое обозначение: неизвестных - последними буквами
латинского алфавита - x, y, z, известных - начальными
буквами того же алфавита - a, b, c, ... и т.д. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы.Слайд 44 Само слово «функция» (от латинского functio -совершение, выполнение)
впервые было употреблено немецким математиком Лейбницем в 1673г. в
письме к Гюйгенсу (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), слово функция было введено в печать с 1694 года.Слайд 45 Поговорим о русских ученых, внесших вклад в развитие
понятия функция. Это Николай Иванович Лобачевский. Заслуги Лобачевского в
других областях математики не так велики, как его геометрическое дело. Но его крупный математический талант проявился и в других исследованиях, например, в исследованиях о сходимости строк.Лобачевский опередил своих современников на несколько десятилетий. Учебник алгебры Лобачевского, изданный им в 1834г. под заглавием: "Алгебра или вычисление конечных" - отличается от других учебников алгебры, не только в России, но и за границей, систематичностью расположения, строгостью изложения основных понятий и замечательной полнотой.
Слайд 46
Соболев Сергей Львович (род. в 1908г.)
Это известный
советский математик, академик.
Его основные труды были посвящены теории
уравнений с частными производными, математической физике, функциональному анализу и вычислительной математике. Им начато систематическое применение функционального анализа в теории уравнений с частными производными.
Соболев ввел понятие обобщенного решения уравнения с частными производными и дал первое (1935 г) строгое определение обобщенной функции;
Слайд 52
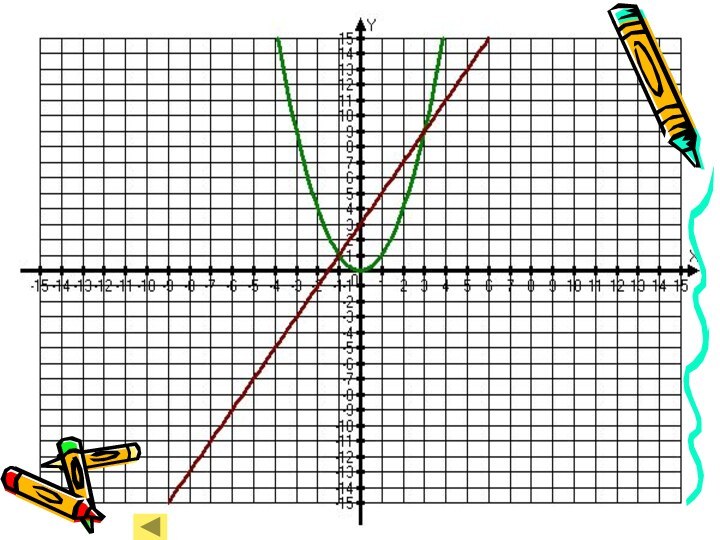
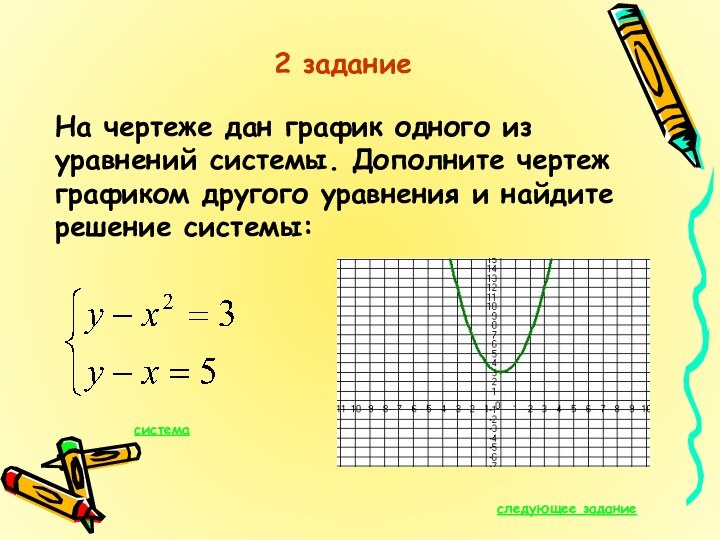
2 задание
На чертеже дан график одного из уравнений
системы. Дополните чертеж графиком другого уравнения и найдите решение
системы:следующее задание
система
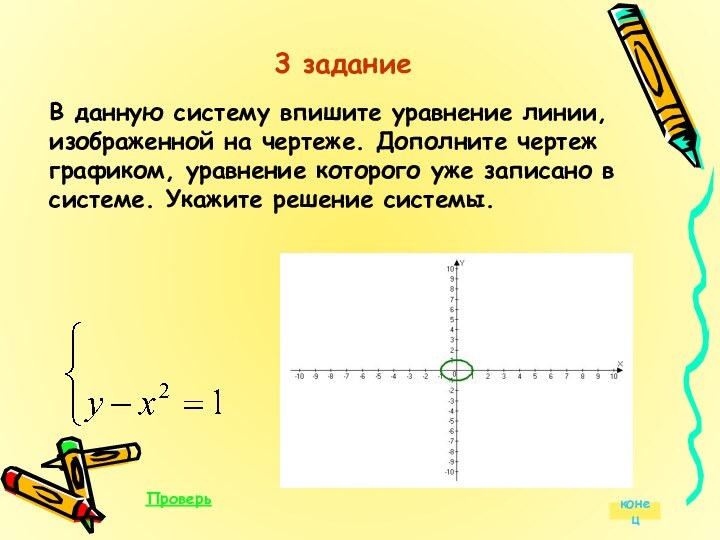
Слайд 55 В данную систему впишите уравнение линии, изображенной на
чертеже. Дополните чертеж графиком, уравнение которого уже записано в
системе. Укажите решение системы.Проверь
конец
3 задание