синусоида
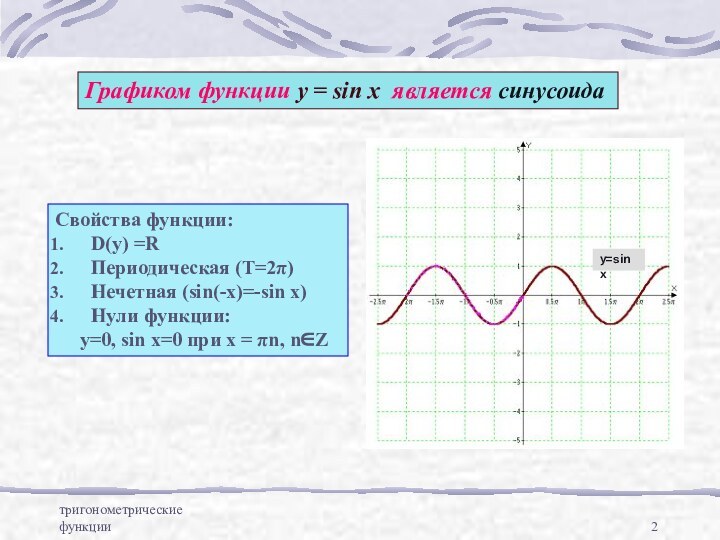
Свойства функции:
D(y) =R
Периодическая (Т=2π)
Нечетная (sin(-x)=-sin x)
Нули функции:
у=0, sin x=0 при х = πn, n∈Zy=sin x
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

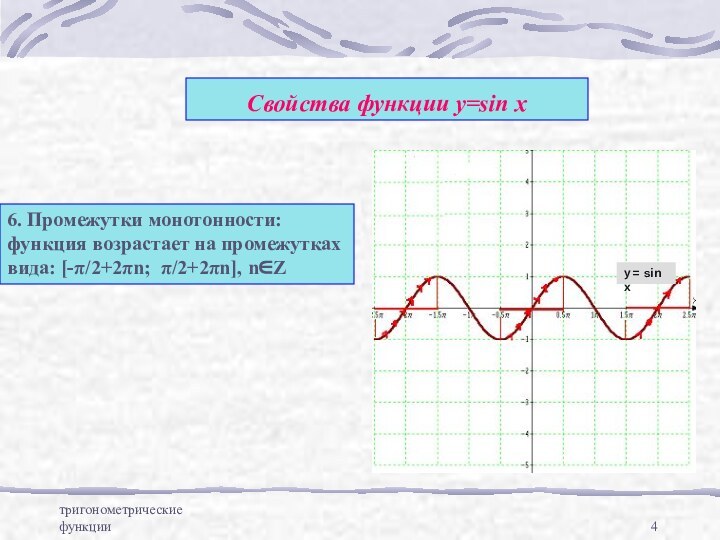
![Графики тригонометрических функций тригонометрические функцииСвойства функции у=sin x Промежутки монотонности:функция убывает на промежуткахвида: [π/2+2πn; 3π/2+2πn], n∈Zy=sin x](/img/tmb/12/1115422/64da4a7853db93836db31914c804b91c-720x.jpg)
![Графики тригонометрических функций тригонометрические функцииСвойства функции у =sin x8. Область значений: Е(у) = [-1;1]y = sin x](/img/tmb/12/1115422/5e904085cf04c7bd9a117e328bc2535c-720x.jpg)


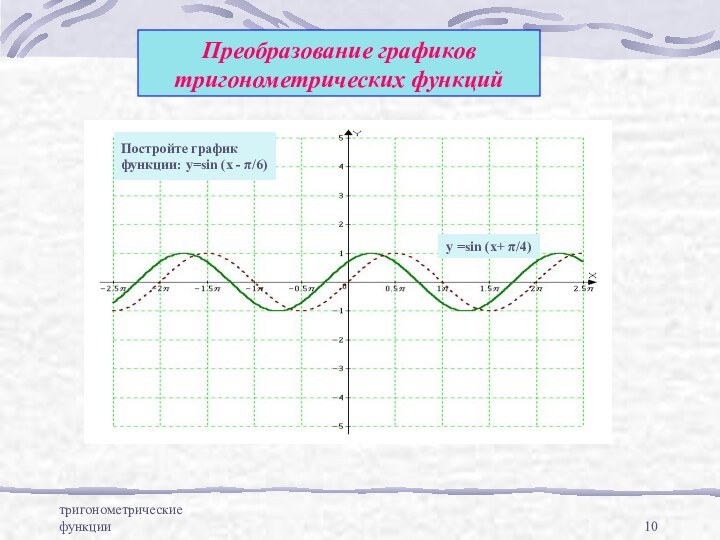
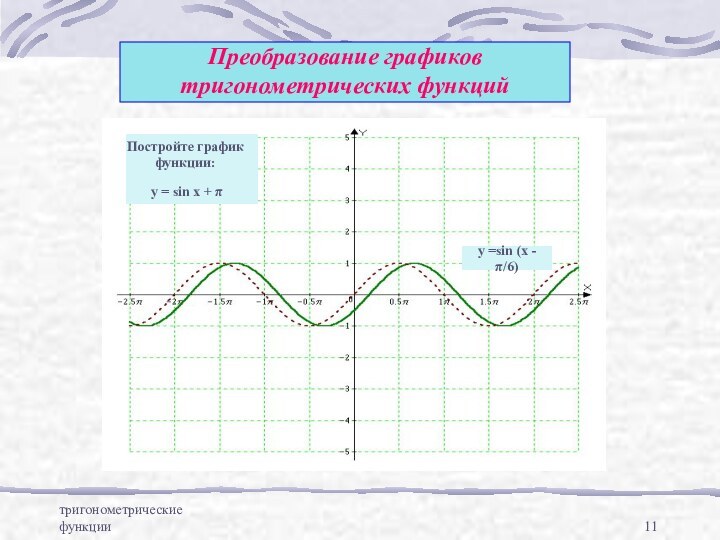
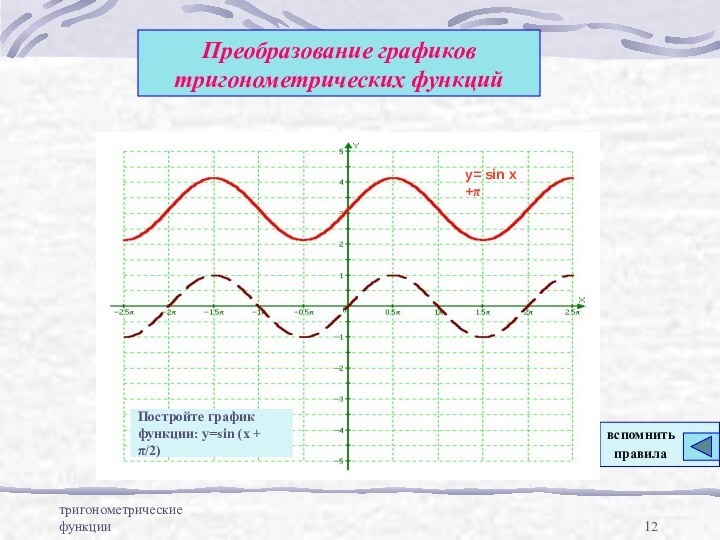




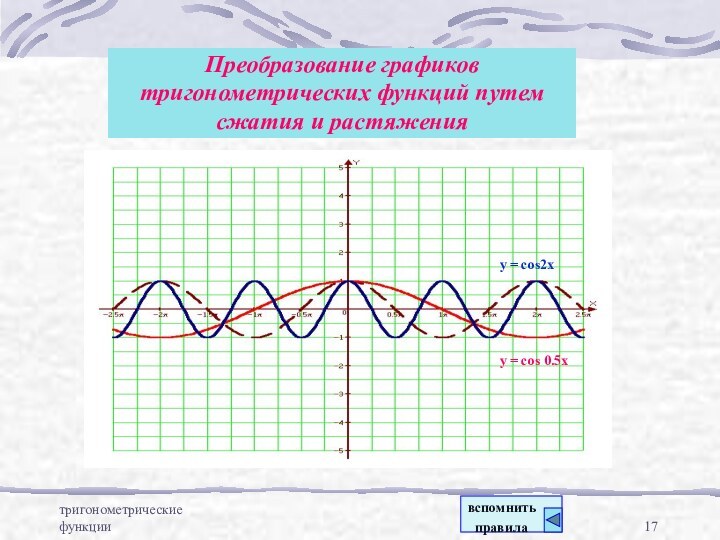



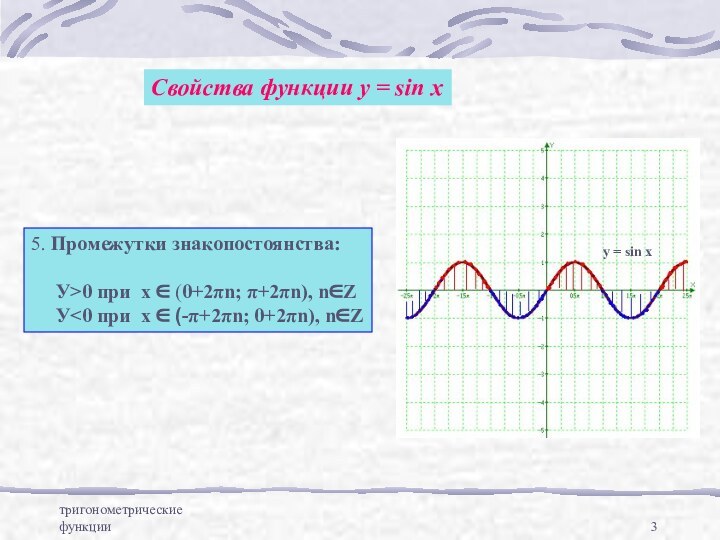
y=sin x
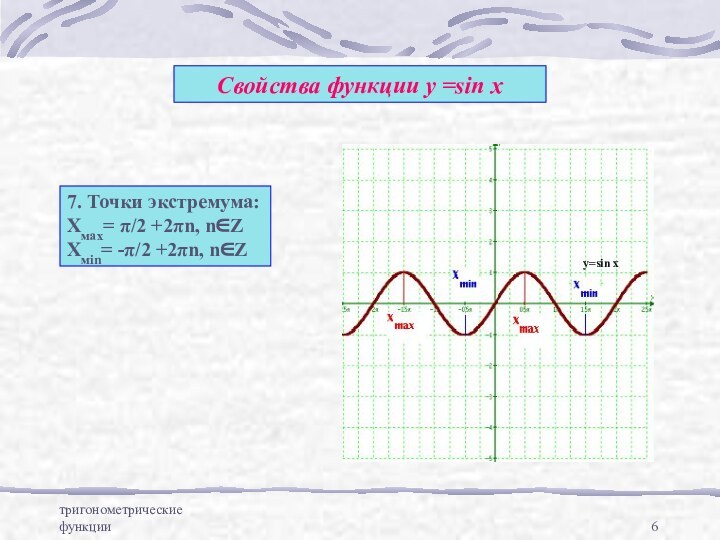
y = sin x