- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Графики тригонометрических функций
Содержание
- 2. Вспомним определение синуса и косинуса угла поворота:sincos
- 3. 00xxyy0111233211Масштаб :3445566На оси абсцисс координатной плоскости Оху
- 4. 0xy1Масштаб :3Таким образом, мы получили график функции
- 5. xy0101Напомним некоторые рациональные значения функции у=sinx на промежутке [−; ]:−1
- 6. xy10Масштаб :3На практике, для построения графика функции
- 7. xy10Масштаб :3−1Используя равенство cosx=sin(
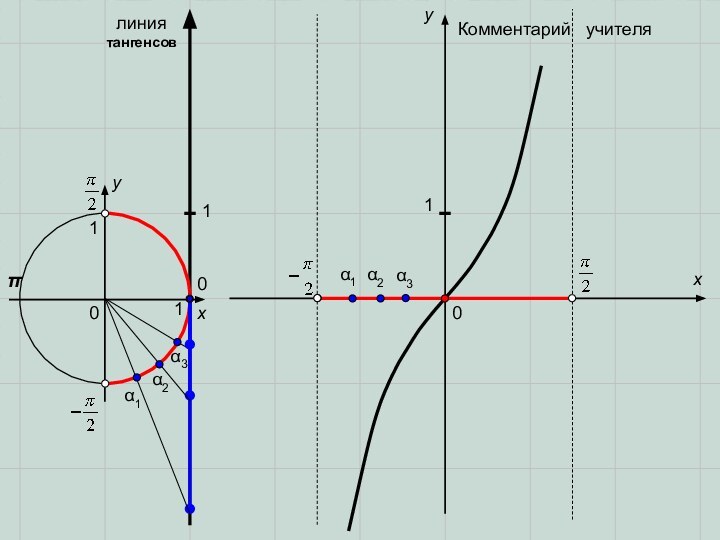
- 8. 00xxyy0111233211линия тангенсов1Комментарий учителя
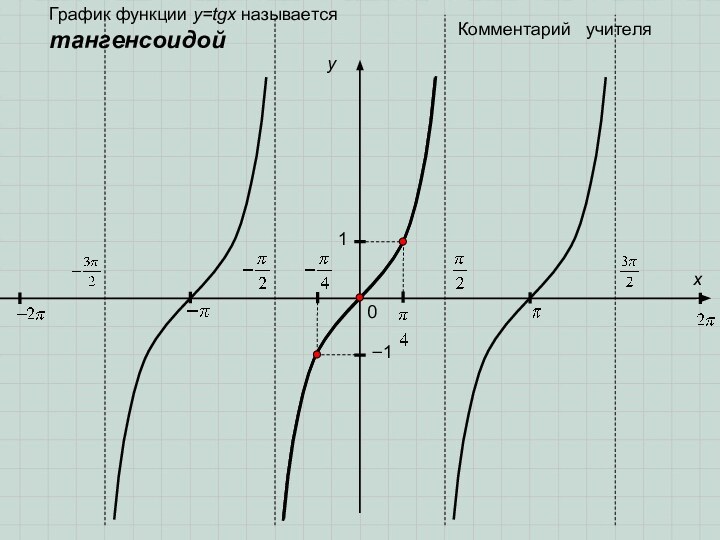
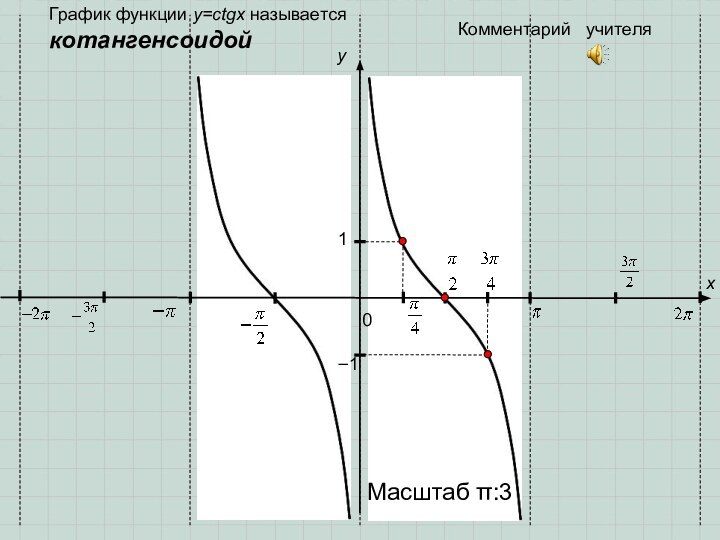
- 9. 0y1x−1Комментарий учителяГрафик функции y=tgx называется тангенсоидой
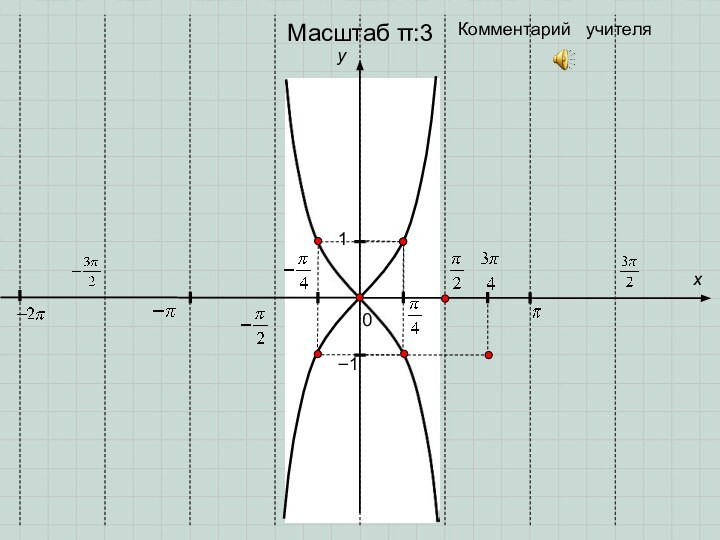
- 10. 0y1x−1Комментарий учителяМасштаб :3
- 11. Скачать презентацию
- 12. Похожие презентации
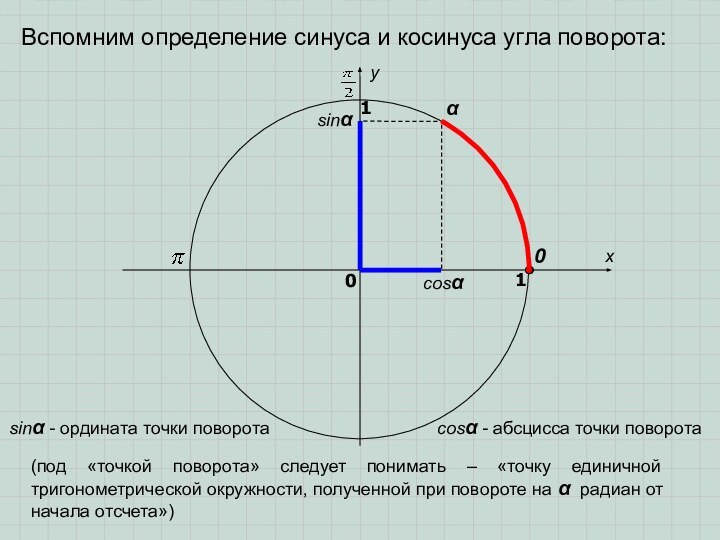
Вспомним определение синуса и косинуса угла поворота:sincos xy0101sin - ордината точки поворотаcos - абсцисса точки поворота(под «точкой поворота» следует понимать – «точку единичной тригонометрической окружности, полученной при повороте на радиан от начала отсчета»)
![Графики тригонометрических функций xy0101Напомним некоторые рациональные значения функции у=sinx на промежутке [−; ]:−1](/img/tmb/13/1270431/3413c8ddebd30eab220523b32a3ad882-720x.jpg)
![Графики тригонометрических функций xy10Масштаб :3На практике, для построения графика функции у=sinx на промежутке [0; ],](/img/tmb/13/1270431/9c3c7ba88c623a8ef65fc7df2b3a398a-720x.jpg)
Слайд 2
Вспомним определение синуса и косинуса угла поворота:
sin
cos
x
y
0
1
0
1
sin
- ордината точки поворота
поворота» следует понимать – «точку единичной тригонометрической окружности, полученной при повороте на радиан от начала отсчета»)
Слайд 3
0
0
x
x
y
y
0
1
1
1
2
3
3
2
1
1
Масштаб :3
4
4
5
5
6
6
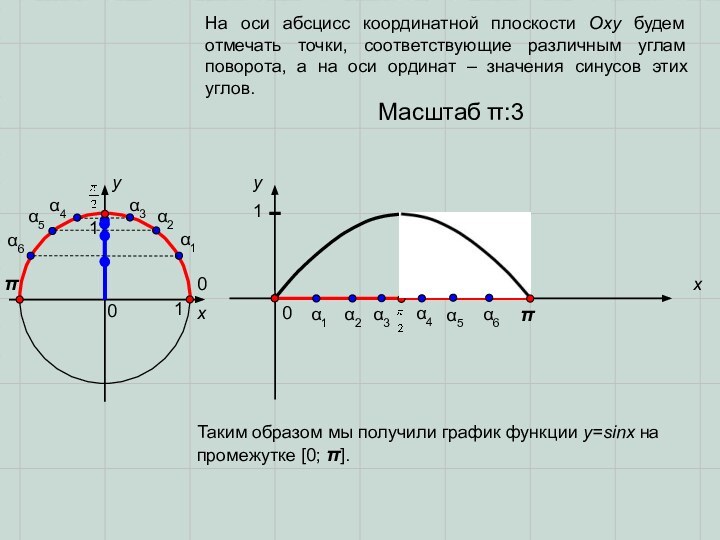
На оси абсцисс координатной плоскости Оху будем
отмечать точки, соответствующие различным углам поворота, а на оси
ординат – значения синусов этих углов.Таким образом мы получили график функции y=sinx на промежутке [0; ].
Слайд 4
0
x
y
1
Масштаб :3
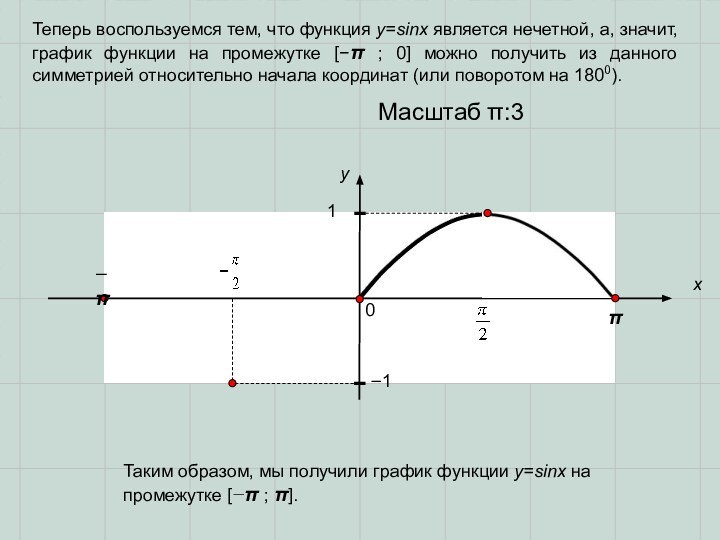
Таким образом, мы получили график функции y=sinx
на промежутке [− ; ].
−1
−
Теперь воспользуемся тем, что функция
y=sinx является нечетной, а, значит, график функции на промежутке [− ; 0] можно получить из данного симметрией относительно начала координат (или поворотом на 1800).
Слайд 6
x
y
1
0
Масштаб :3
На практике, для построения графика функции у=sinx
на промежутке [0; ], сначала отмечают точки с координатами
(0; 0), ( /6; 0,5), ( /2; 1), ( 5/6; 0,5) и ( ; 0). Они образуют своеобразную «арку», которая периодически (с периодом ) отображается симметрично оси Ох.После этого используют свойство периодичности функции у=sinx. Так как наименьший положительный период функции y=sinx равен 2, то изображенный участок графика можно параллельно переносить влево и вправо вдоль оси Ох на 2n (n) единичных отрезков.
−1
График функции y=sinx называется синусоидой.
Слайд 7
x
y
1
0
Масштаб :3
−1
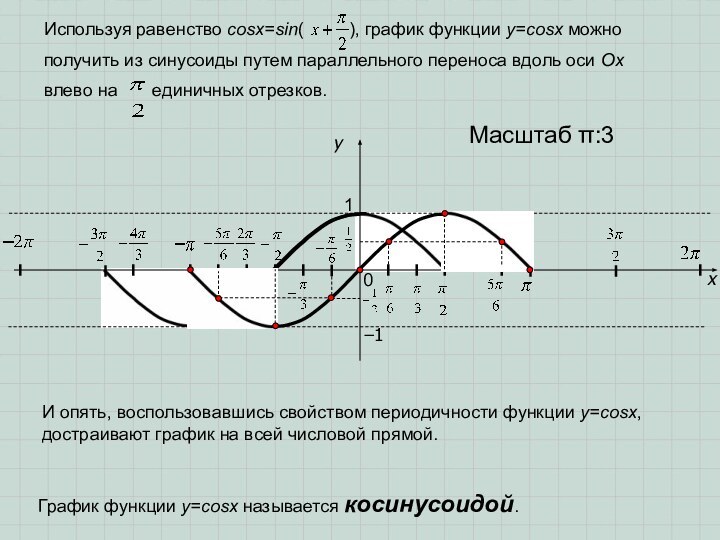
Используя равенство cosx=sin(
), график функции у=cosx можно
получить из синусоиды путем
параллельного переноса вдоль оси Ох влево на единичных отрезков.
И опять, воспользовавшись свойством периодичности функции y=cosx, достраивают график на всей числовой прямой.
График функции y=cosx называется косинусоидой.





























