- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему I Функция У=АХ², её график и свойства
Содержание
- 2. А=1У=Х ²
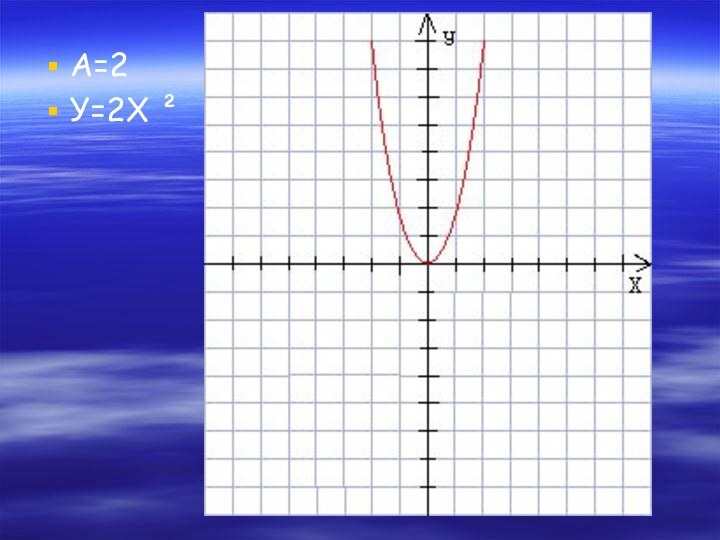
- 3. А=2У=2Х ²
- 4. У=Х²У=2Х²Растяжение от оси Х в два раза
- 5. А=0.5У=Х²У=0.5Х²Сжатие по оси Х в два раза
- 6. Вообще график функции У=АХ² можно получить из
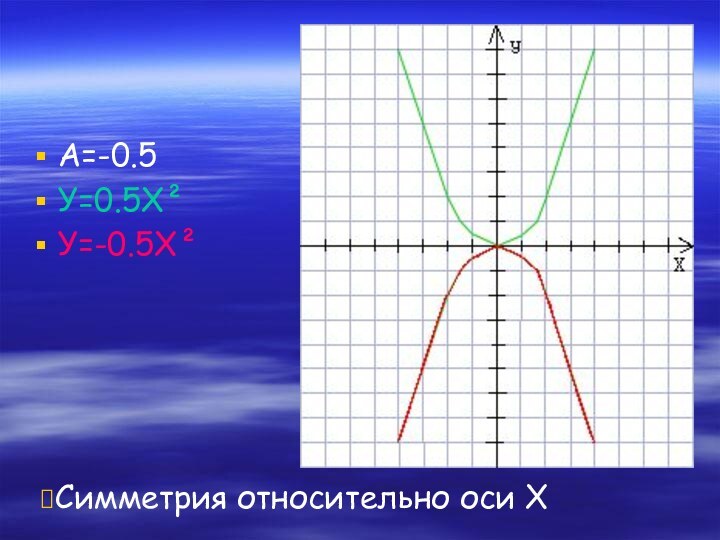
- 7. А=-0.5У=0.5Х²У=-0.5Х²Симметрия относительно оси Х
- 8. Вообще графики функций У=АХ² и У=
- 9. Свойства функции У=АХ² при А>0 Если Х=0,
- 10. Свойства функции У=АХ² при А
- 11. Скачать презентацию
- 12. Похожие презентации
А=1У=Х ²









Слайд 8
Вообще графики функций У=АХ² и
У=
- АХ² (при А не равном нулю) симметричны относительно
оси Х.
Слайд 9
Свойства функции У=АХ² при А>0
Если Х=0, то
У=0. График функции проходит через начало координат.
Если Х не
равно нулю, то У>0. График функции расположен в верхней полуплоскости. Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси У.
Функция убывает в промежутке от минус бесконечности до нуля (включительно) и возрастает в промежутке от нуля (включительно) до плюс бесконечности.
Наименьшее значение, равное нулю, функция принимает при Х=0, наибольшего значения функция не имеет областью значении функции является промежуток от нуля (включительно) до плюс бесконечности.
Слайд 10 Свойства функции У=АХ² при А
У=0. График функции проходит через начало координат.
Если Х не
равно нулю, то У<0. График функции расположен в верхней полуплоскости. Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси У.
Функция возрастает в промежутке от минус бесконечности до нуля (включительно) и убывает в промежутке от нуля (включительно) до плюс бесконечности.
Наибольшее значение, равное нулю, функция принимает при Х=0, наименьшего значения функция не имеет областью значении функции является промежуток от минус бесконечности до нуля (включительно).