- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Игра как эффективная форма развития познавательного интереса учащихся к математике
Содержание
- 2. Игра как эффективная форма развития
- 4. Актуальность:Увеличение умственной нагрузки заставляет задуматься над тем,
- 5. Цель работы : Обосновать целесообразность игр
- 6. М а т е м а т
- 7. Виды математических игр
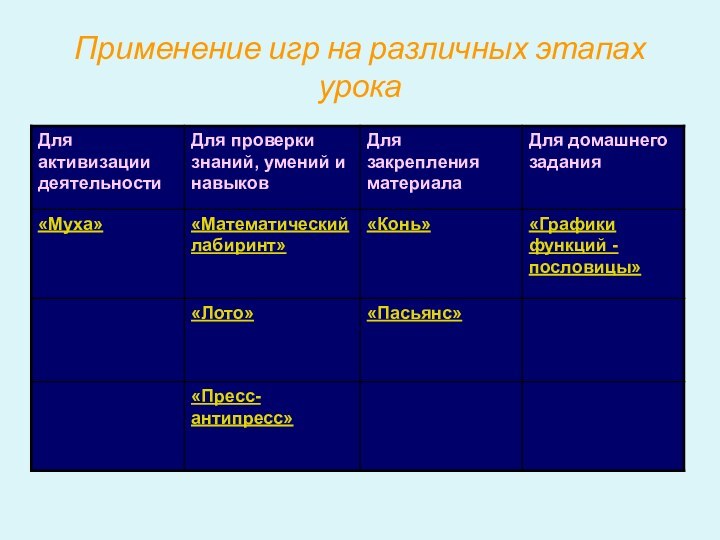
- 8. Применение игр на различных этапах урока
- 9. Результативность применения игровых технологий.Диаграмма качества обучения в
- 10. Заключение Из
- 11. Игра «Муха»
- 12. Математический лабиринт «Лабиринт» - это несколько заданий,
- 13. «Лото»
- 14. «Пресс-антипресс» У игроков есть перечень
- 15. «Конь»
- 16. «Пасьянс» (8
- 17. Скачать презентацию
- 18. Похожие презентации
Игра как эффективная форма развития познавательного интереса учащихся к математике. Работу выполнила:














Слайд 3
«Игра- это искра, зажигающая огонек пытливости и любознательности» В.А. Сухомлинский
Главная идея работы:
Может ли игра являться эффективной формой развития познавательного интереса учащихся к математике?
Признаки учебной игры, предложенные В.М. Букатовым:
Дидактическая цель ставиться перед учащимися в форме игровой деятельности;
Учебная деятельность подчиняется правилам игры;
Учебный материал используется в качестве средства игры;
Успешное выполнение задания связывается с игровым результатом.
Слайд 4
Актуальность:
Увеличение умственной нагрузки заставляет задуматься над тем, как
поддержать интерес учащихся к изучаемому материалу, их активность на
протяжении всего урока.Взаимозависимость всех разделов предмета, нетерпимость к пробелам, как в целом, так и в частях является причиной неуспехов учащихся в обучении.
Однообразная деятельность, рассчитанная на механическое запоминание, не может вызвать интереса. Отсутствие положительных эмоций может привести к пассивности.
Математические игры разнообразны, требуют
самостоятельности, эмоционально насыщены.
Слайд 5
Цель работы :
Обосновать целесообразность игр на разных
этапах изучения математического материала.
Задачи:
1.Определить цели, задачи и функции математической
игры.2. Рассмотреть виды математических игр.
3. Показать, как учебный материал можно использовать в качестве средств игры.
Слайд 6
М
а
т
е
м
а
т
и
ч
е
с
к
а
я
и
г
р
а
Цели: развитие мышления; углубление теоретических
знаний; самоопределение в
мире увлечений и
профессий; воспитание сотрудничества и
коллективизма; развитие волевых качеств;
приобретение
новых знаний, умений и навыков; Формирование адекватной самооценки; контроль
знаний; мотивация учебной деятельности.
Задачи: образовательные, развивающие,
воспитательные.
Функции: обучающая, развлекательная,
коммуникативная, релаксационная.
Слайд 7
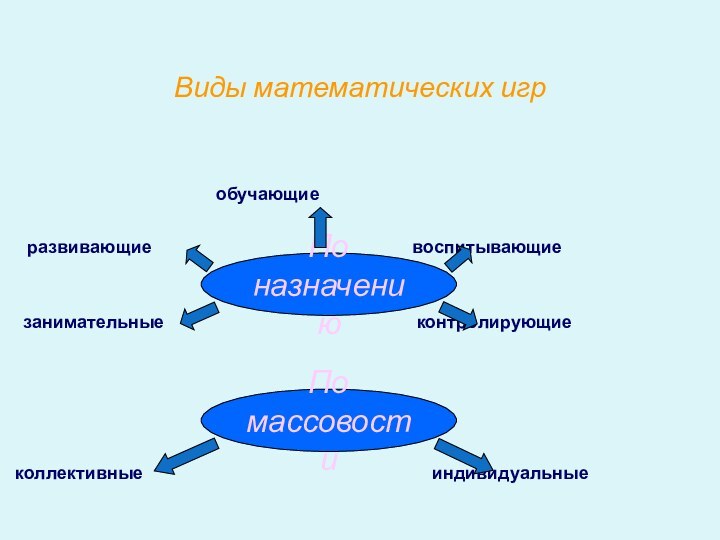
Виды математических игр
обучающие
развивающие воспитывающие
занимательные контролирующие
коллективные индивидуальные
По назначению
По массовости
Слайд 9
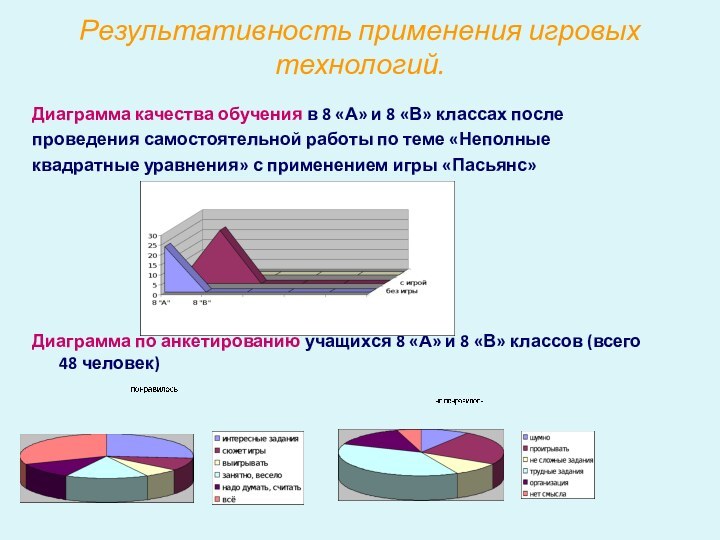
Результативность применения игровых технологий.
Диаграмма качества обучения в 8
«А» и 8 «В» классах после
проведения самостоятельной работы по
теме «Неполныеквадратные уравнения» с применением игры «Пасьянс»
Диаграмма по анкетированию учащихся 8 «А» и 8 «В» классов (всего 48 человек)
Слайд 10
Заключение
Из изложенного
можно сделать вывод, что математическая игра повышает интерес к
предмету, вносит разнообразие и эмоциональную окраску в учебную работу, снимает утомление, развивает внимание, сообразительность.Игра дает возможность проявить себя, свои способности, проверить имеющиеся знания, приобрести новые, и все это в необычной занимательной форме. Использование игр на разных этапах изучения различного по характеру математического материала является эффективным средством активизации познавательной деятельности учащихся.
Новизна опыта в усовершенствовании, модернизации и адаптации к конкретным условиям уже известных средств обучения. Использование компьютера значительно облегчает подготовительный процесс и делает восприятие более активным.
Адресная направленность: опыт по использованию игры как средства развития познавательного интереса может применяться при изучении различных предметов, также использоваться во внеурочное время. Его можно применять в основной и старшей школе всех уровней. Он будет интересен учителям разных специальностей.
Слайд 11
Игра «Муха»
( 8 класс, тема «Арифметический квадратный корень».)
Правила игры: составляется таблица 3 × 3 с числами (на слайде или на бумажном носителе). Столбцы и строки подписаны. Задача учащихся следить за движением мухи, которая перелетает с клетки на клетку. Учителем называются только координаты клетки, а число не произносится вслух. Задача учащихся: вычислить или найти сумму.
Слайд 12
Математический лабиринт
«Лабиринт» - это несколько заданий, соединенных
таким образом, что ответ одного задания служит номером другого.
Игра начинается за 15-20 минут до конца урока. В результате решения получается цепочка чисел, по которой, как по ориентиру, ученик (группа) выходит из лабиринта. Перечень таких цепочек – чисел для каждой команды должен быть записан у учителя. Это позволит следить за успешностью прохождения лабиринта отдельными учащимися или командой.Математический лабиринт по теме: «Решение уравнений», 7 класс.
Учащиеся получают бланк с заданием:
№ 1. 4 (1 – 0,5а) = -2 (2а – 3)
№ 2. 4 (3 - х) – 11 = 7 (2х – 5)
№ 3. –5 (0,8 а + 1,2) = -а – 18
№ 4. 4 (3х – 8) = 3 (5 – х) + 13
№.5 5y/12-3/4=1/2
№ 6 ( x+2)/3=(2x+3)/5
№ 7 -3,2 в + 2,4 = -2 (1,2в + 2,4) = 9
№ 8 2(7x+21)/7-(3x+6)/3=9
№ 9. 1,2 (3х + 5) = 2 (2,4 х – 3,6)
№ 10. 0,3 (5х – 7) = 3 (0,2х + 3,2)
№ 11. 0,5у – 0,6 = 0,1у + 0,2
№ 12. –3 (2,1х – 4) – 4,2 = 1,2 (-5х + 0,5)
№ 13. x/2=x/3+1
Вход в лабиринт:
I команда начинает с уравнения № 8
II команда - № 7
III команда - № 10
Выход из лабиринта: полученный ответ совпадает с номером задания.
Ключ к лабиринту: I команда: 8 5 3 4
II команда: 7 9 11 2
III команда: 10 13 6 1
Побеждает та команда, которая первая пройдет лабиринт.
Слайд 13
«Лото»
(8 класс, тема «Квадратные корни»)
В специальном конверте учащимся предлагается набор карточек. Обычно их больше, чем ответов на большой карте, которая тоже вложена в конверт. Ученик достает из конверта карточку, решает пример и накрывает ею соответствующий ответ. Карточки накладываются лицевой стороной вниз. Если все примеры решены правильно, то обратные стороны составляют какой-то условный шифр: рисунок, чертеж, код (я обычно беру комбинацию цифр). Учитель, проходя по рядам, легко определяет результаты работы.
Ответы : Код:
Использование компьютеров позволяет немного изменить правила игры в лото.
Учителю нужно подготовить несколько больших карт, разделенных на прямоугольники с записанными в них ответами, маленькие карточки с шифром и соответственное количество заданий на слайде. Разбить класс на группы по 4-5 человек. Учитель показывает слайд. Та группа, которая обнаружила на большой карте ответ и считает его правильным, забирает карточку с шифром и накрывает ею соответствующую клеточку шифром вверх. Выигрывает та группа, которая больше всех накрыла правильно.
Слайд 14
«Пресс-антипресс»
У игроков есть перечень вопросов,
по которым будет проходить пресс – конференция. На первый
ряд предлагается сесть тем, кто оценивает свои знания на «3», на второй ряд – на «4», на третий ряд – на «5». Вопросы также разделены по уровням сложности. Право отвечать первым всегда предоставляется первому ряду (кто на «3»). Когда возможные варианты ответов с этого уровня прозвучали, право дополнить дается тем, кто сидит на втором, а затем и на третьем ряду. Если кому-то с первого ряда удается ответить на вопрос более сложного уровня так, что дополнить нечего, то учитель может пересадить его на второй или третий ряд. В зависимости от степени и качества участия в ответах, учащиеся могут повышать или понижать свой ранг, пересаживаясь по решению учителя. Есть еще одна версия этой игры - идеальный зачет. Он происходит неожиданно для участников. Учащиеся размещаются согласно притязаниям на итоговую оценку, замирают в ожидании вопросов, а учитель объявляет…, что вопросов не будет и сразу готов поставить заказанные отметки. Таким образом, эта игра может выполнять релаксационную функцию.
Слайд 15
«Конь»
( 6 класс, тема «Сложение чисел с разными знаками).
Игра – индивидуальная. Каждый ученик получает таблицу, накрытую калькой и «коня» (им может быть картонный кружочек). Играющему нужно провести «коня» от линии старта к линии финиша. Ход можно начать с любого места на старте. «Конь» двигается так, как на шахматной доске. Но здесь надо соблюдать условие: число, записанное в клетке старта или там, где стоит «конь» сложенное с числом из клетки, где «конь» делает поворот, должно дать число, которое записано в клетке куда «прыгает» «конь». Некоторые клетки могут оказаться «фальстартом». На кальке показать ход «коня».
Слайд 16
«Пасьянс»
(8 класс,
тема: «Неполные квадратные уравнения».)
Пасьянс содержит
20 карточек, на которых написано 10 уравнений и ответов к ним (уравнения - на одной карточке, ответы - на другой). Эти карточки раскладываются в 4 ряда по 5 карточек в каждом ряду. Карточки можно брать по 2 либо по вертикали, либо по горизонтали. Каждая пара считается удачей, если она составляет верное решение.Удачные пары:





























