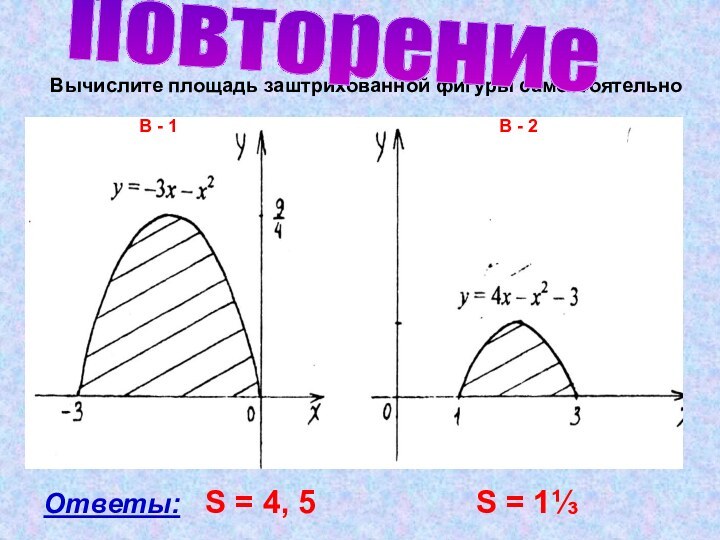
S = 4, 5
S = 1⅓Повторение
В - 1
В - 2
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

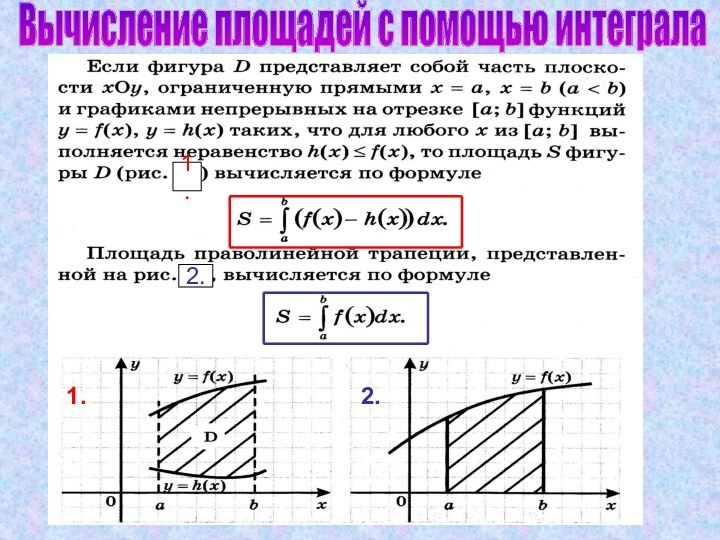
![Интеграл Другой подход к вычислению площади криволинейной трапецииОтрезок [а;в] разбит на n отрезков](/img/tmb/14/1394182/830d8e7c00b61b348057085e9cccc4a1-720x.jpg)
![Интеграл Определение интегралаДля любой непрерывной на отрезке [ а; в ] функции f](/img/tmb/14/1394182/587ea8ca2c052027e5940580b2041bce-720x.jpg)









Повторение
В - 1
В - 2
В силу непрерывности f объединение построенных прямоугольников при большом n «почти совпадает» с криволинейной трапецией.
Sn -> S при n -> ∞.
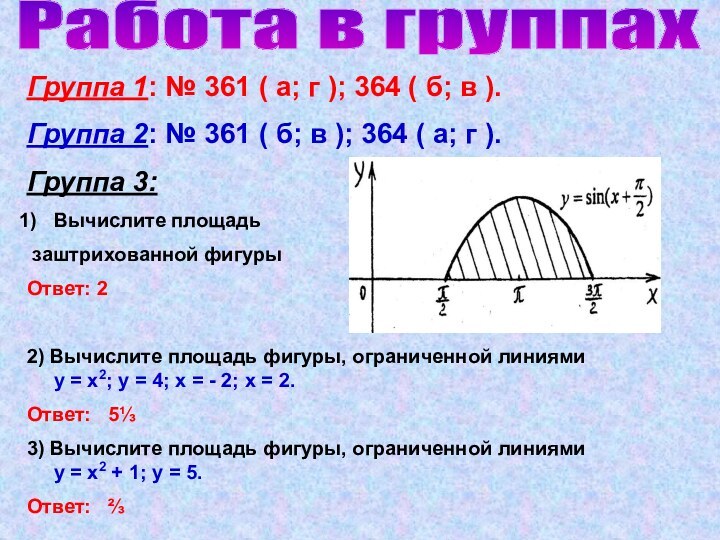
2. Вычислить интеграл от - π/4 до π функции f ( х ) = 3 cos 2х.
3. Вычислить площадь фигуры, ограниченной линиями f1 ( х ) = х2 ; f2 ( х ) = 2х
4. Вычислить площадь фигуры, ограниченной линиями: х = 0; у = х2 – 4х + 5 и касательной к этому графику в точке х0 = 2.